Цель работы
Изучение методики расчета оптимального по быстродействию программного управления для объекта, динамика которого описывается линейным дифференциальным уравнением второго порядка без позиционного члена, и моделирование системы на ЭВМ с найденным оптимальным управлением.
Содержание работы
2.1. Изучение теоретических основ расчета оптимальных быстродействий на основе принципа максимума.
2.2. Определение алгоритма оптимального управления и расчет моментов переключения управления.
2.3. Моделирование системы с найденными управлениями.
2.4. Выводы.
Теоретические основы работы
Задано дифференциальное уравнение функционирования объекта управления в виде:
(6.1)
где 
- управления, причем предполагается,
(6.2)
Необходимо перевести объект (6.1) из состояния:
(6.3)
в другое состояние:
(6.4)
за минимальное время T, не нарушая ограничение (6.2).
Путем введения новых переменных:
исходное дифференциальное уравнение (6.1) приводится к системе вида:
Для данной системы составляется гамильтониан:
и дифференциальные уравнения для сопряженных переменных:
(6.5)
Из условия: 
определяется закон оптимального управления
(6.6)
После анализа решения 
, полученного в явном виде из (6.5) через произвольные постоянные, делается заключение о характере управления (6.6).
Расчет типового примера
Определим момент 
переключения управления и интервал моделирования Т для уравнения (6.1), считая, что 
.
Решение уравнения (1) можно представить в виде:
(6.7)
где 
- произвольные постоянные на i – м участке управления, i=1,2. На первом участке управления, при наших граничных условиях будет 
. Тогда подставляя начальные условия (6.3) при t= 0 в систему (6.7), получаем при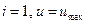 
:
(6.8)
Аналогично, подставляя конечные условия (6.4) при t = Т в (6.7), получаем при i = 2:
. (6.9)
«Сшиваем» решения системы (6.7) в момент 
:
(6.10)
Подставляя в (6.10) значения (6.8) и (6.9), получаем:
Из второго уравнения системы получаем:
Из первого уравнения определяем интервал Т:
Согласно (6.11) 
. (6.12)
Подставляя (6.12) в (6.11) окончательно получаем трансцендентное уравнение для определения 
:
Введя обозначение 
, преобразуем последнее уравнение к виду:
. (6.13)
Из уравнения (6.12) находим 
. Пусть, например, 
, тогда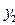 
не является решением уравнения (6.13), поэтому 
.
Таким образом, программное во времени управление, оптимальное по быстродействию, выглядит так:
Порядок выполнения работы
1. Применив стыковку решений дифференциального уравнения (6.1) в момент переключения управлений между своими предельными значениями 
, определить этот момент и время Т, применяя при необходимости для решения трансцендентного уравнения ЭВМ и учитывая, что для некоторого сочетания граничных условий интервал управления может быть один, т. е. переключения управления не будет.
2. Промоделировать на ЭВМ систему (6.1) с найденным оптимальным программным по времени управлением 
и начальным условием (6.3), применив метод Рунге-Кутта и выбрав шаг исходя из полученных значений и Т (
) [2].
3. Построить графики оптимального управления и оптимальной траектории движения объекта x(t), 
. Сделать выводы.
7. Содержание отчёта
1. Постановка задачи.
2. Расчет момента переключения управлений и времени Т в оптимальном процессе для варианта исходных данных. Текст программы трансцендентного уравнения.
3. Текст программы моделирования системы (6.1) с оптимальным управлением.
4. Результаты моделирования для варианта начальных данных в виде графиков 
.
5. Выводы.
Варианты заданий
| № варианта | a | b | 
| 
| 
| 
| 
|
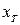
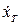
| 0.62 | 0.0023 | 2.09 | |||||
| 0.5 | 0.1 | ||||||
| 0.88 | 0.016 | 3.66 | |||||
| 2.05 | 1.5 | ||||||
| 0.5 | -1 | ||||||
| 1.43 | 0.068 | -1 | -1 | ||||
| 0.18 | |||||||
| 2.11 | 0.65 | 3.5 | |||||
| 0.33 | 0.42 | -1 | |||||
| 2.15 | 0.245 | 1.5 | |||||
| 0.67 | 0.67 | 0.0043 | |||||
| 0.55 | 0.12 | 2.5 | |||||
| 0.77 | 0.025 | 3.25 | |||||
| 1.2 | 1.5 | ||||||
| 3.3 | 0.8 | -1 |
Литература
1. Иванов В.А., Фалдин Н.В. Теория оптимальных систем автоматического управления. – М.: Наука, 1981. - 331с.
2. Демидович Б.П. и др. Численные методы анализа. - М.: Наука, 1968. - 367с.
