Теоретические основы работы

 

Пусть поведение некоторой САУ описывается системой уравнений вида:

(3.1)

или, в векторной форме:

 

где , (3.2)

 

причем будем полагать, что

,

.

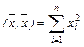Решение системы (3.2) называется устойчивым по Ляпунову, если для любого существует такое , что для всякого решения той же системы, начальное значение которого удовлетворяет неравенству

, (3.3)

при всех выполняется неравенство

.

Если же для некоторого такого не существует, то решение называется неустойчивым.

Решение называется асимптотически устойчивым, если оно устойчиво по Ляпунову и, кроме того, все решения с достаточно близкими начальными условиями неограниченно приближаются к при , т.е. если из неравенства (3.3) следует выполнение условия

при .

Наличие или отсутствие устойчивости не зависит от выбора .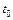

Вопрос об устойчивости данного решения системы (3.2) можно свести к исследованию на устойчивость нулевого (тривиального) решения 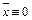некоторой системы, аналогичной системе (3.2)

где .

Решение 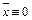называют невозмущенным движением. Приведем оценки устойчивости линейной системы

(3.4)

по корням характеристического уравнения

(3.5)

где E - единичная матрица.

1. Если вещественные части всех корней характеристического уравнения (3.5) отрицательны, то невозмущенное движение 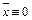системы (3.4) асимптотически устойчиво (или говорят, что сама система (3.4) асимптотически устойчива).

2. Если среди корней характеристического уравнения (3.5) имеется хотя бы один с положительной вещественной частью, то система (3.4) неустойчива.

3. Если некоторые корни характеристического уравнения имеют нулевые вещественные части, а остальные корни имеют отрицательные вещественные части, то в случае простых (некратных) корней с нулевыми вещественными частями система будет не асимптотически устойчива, во всех остальных случаях требуется дополнительное исследование.

 

Теорема (Критерий Гурвица). Необходимым и достаточным условием асимптотической устойчивости системы (3.4) является положительность всех главных миноров матрицы размера :

,

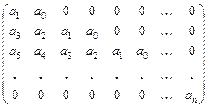составленной из коэффициентов характеристического уравнения (3.5), приведенного к виду

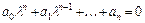. (3.6)

Матрица Гурвица строится следующим образом. В первом столбце выписываются все нечетные коэффициенты характеристического уравнения, начиная с . Затем каждая строка матрицы дописывается последовательно коэффициентами с уменьшающимися номерами вплоть до , после чего дописываются нули так, чтобы общее количество элементов в строке равнялось n.

При этом определители Гурвица имеют вид

.

Таким образом, условие Гурвица гласит:

Для асимптотической устойчивости решения уравнения (3.4) необходимо и достаточно, чтобы выполнялись соотношения:

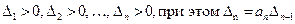
Замечание. При вычислении главных миноров можно воспользоваться следующим способом.

Пусть, например, требуется вычислить

,

элемент матрицы, получаемый на k -той итерации, где - i- й ведущий.

При этом

причем

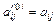
При большом порядке уравнения (3.6), наибольшее применение имеет критерий устойчивости Рауса как наиболее простой при реализации алгоритм.

Для характеристического уравнения вида (3.6) составляется таблица Рауса (табл.3.1).

 

Таблица 3.1

 

				…
				…
				…
				…
…	…	…	…	…

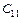
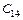
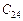
При этом, в первые две строки записываются коэффициенты характеристического уравнения:

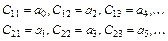
коэффициенты, начиная с , вычисляются по формуле

.

Для обеспечения устойчивости системы требуется выполнение условия

.

Исследование устойчивости линейной системы автоматического управления, характеристическое уравнение которого имеет вид

, (3.7)

можно проводить с помощью достаточных условий устойчивости, оцениваемых в параметрах:

. (3.8)

Для того, чтобы система с характеристическим уравнением (3.7) была устойчивой, необходимо выполнение неравенств в следующем порядке

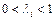, (3.9)

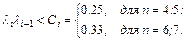
Для того, чтобы система с характеристическим уравнением (3.7) была устойчивой, достаточно выполнение неравенств:

(3.10)

(3.11)

При анализе устойчивости линейной системы по ее характеристическому уравнению можно рекомендовать следующий алгоритм расчета:

 

1. Проверяются знаки коэффициентов характеристического уравнения (3.7). Если хотя бы один из коэффициентов характеристического уравнения будет отрицательным или равным нулю, то можно сразу сказать, что система неустойчива.

2. Если все положительны, то вычисляется параметр

.

Если для всех выполняется необходимое условие устойчивости (3.9), то переходим кп. 3, в противном случае система неустойчива.

 

3. Если все меньше величины 0.465, то выполняется достаточное условие (3.10) и система устойчива. В противном случае переходим на следующий пункт.

 

4. Для каждой соседней пары значений получаем величину . Если полученная сумма меньше 0,89, товыполняются достаточные условия устойчивости (3.11), и система устойчива. В противном случае переходим на следующий пункт.

 

5. Для каждой соседней пары значений рассчитываем величину . Если хотя бы одно произведение больше значения для соответствующих n и i, то система неустойчива.

 

Порядок выполнения работы

1. Изучить теоретическую часть работы.
2. Для представленного дифференциального уравнения, описывающего работу системы автоматического регулирования (САР), составить характеристический многочлен вида (2.6).
3. Пользуясь критерием устойчивости Рауса – Гурвица, исследовать на устойчивость невозмущенное движение САР.
4. Исследовать на устойчивость невозмущенное движение САР, используя достаточный критерий устойчивости.
5. Объяснить полученные результаты. Сделать выводы.

 

Варианты заданий

5.1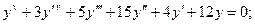

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

6. Содержание отчёта

1. Постановка задачи.
2. Порядок выполнения работы.
3. Краткая теория.
4. Алгоритм решения задачи.
5. Расчет тестового примера.
6. Программа расчета.
7. Результаты решения задачи.
8. Список используемой литературы.

 

Литература.

1. Меркин Д.Р. Введение в теорию устойчивости движения. – М.: Наука, 1981. – 312с.
2. Малкин И.Г. Теория устойчивости движения. - М.: Наука, 1972. – 530с.