Банк задач
Математика
III семестр
ГРФ 2012-2013
Модуль 1 Кратные, криволинейные интегралы.
1. Найти площадь фигуры, ограниченной линиями Д: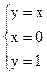 
.
2. Найти площадь фигуры, ограниченной линиями: y = 5 - x2; y = 1.
3. Вычислить:
4.
 |
Найти площадь фигуры, ограниченной линиями:
.
5. Найти площадь области, ограниченной линиями y = ln(3x), x=1/3, x=e.
6. Вычислить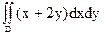 
, D: y=x3, x=0, y=1.
7. Вычислить 
8. Вычислить 
9. Вычислить 
.
10. Найти объем тела, ограниченного поверхностями
11. 
Вычислить 
, если контур С: y=2x2; от (.) А(1,2) до (.) В(2,8).
12. Вычислить 
по контуру С: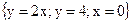 
.
13. Вычислить 
, где С: x2+y2=4, z=1
14. Вычислить интеграл ∫γ(x2y-3x)dx+(y2x+2y)dx
x=3cos t
где γ дуга эллипса y=2sin t t є, [0,π]
15. Вычислить 
, вдоль ломаной ABC, где А(1,2), В(1,5), С(3,5).
Модуль 2 Поверхностные интегралы. Элементы теории поля.
16. Дана функция U(A)=U(x,y,z) 
и точки A1(1;-1;2), A2(3;4;-1)
Вычислить:
А) производную этой функции в точке A1 по направлению вектора 
;
В) grad U(A1).
17. Найти векторные линии векторного поля F=xί+yј
18. Найти div 
, если 
.
19. Найти rot , если 
.
20. 
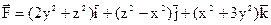. Найти rot 
.
21. 
. Найти rot(rot 
).
22. Установить потенциальность поля 
и найти его потенциал.
23. Установить соленоидальность векторного поля 
. Найти векторный потенциал.
24. Проверить, является ли векторное поле потенциальным, соленоидальным. 
.
25. С помощью формулы Остроградского - Гаусса вычислить поток поля =(x+y, x-z, 2y-2z) через поверхность пирамиды: x=0, y=0, z=0, 2x-3y+3z+6=0.
26. Найти поток векторного поля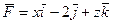 
через часть плоскости p:x+2y+3z=1, расположенную в I октанте.
27.
 |
Найти циркуляцию векторного поля
 |
вдоль контура
28.
 |
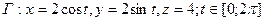Найти работу силового поля
вдоль дуги параболы y=x2- 2x- 3 от т. А(0, -3) до т. В(3, 0).
29. Найти циркуляцию векторного поля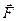 
по замкнутому контуру С, образованному пересечением плоскости (р) с координатными плоскостями, и поток поля 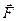через поверхность пирамиды, образованной плоскостями (р), x=0, y=0, z=0 в направлении внешней нормали к ее поверхности: 
.
30. 
. Найти grad(div ).
Модуль 3 Элементы гармонического анализа. Ряды. Численные методы. (Основы вариационного анализа.- самостоятельно)
Ряды
31. Исследовать сходимость ряда 
.
32. Исследовать сходимость ряда 
.
33. Исследовать сходимость ряда: 
34. Исследовать сходимость ряда: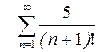 
35. Исследовать на абсолютную или условную сходимость 
36. Исследовать сходимость ряда 
.
37. Исследовать сходимость знакочередующегося ряда 
38. Найти область сходимости степенного ряда 
.
39. Найти область сходимости степенного ряда 
40. Найти интервал сходимости и исследовать сходимость на концах интервала 
41. Разложить в ряд Тейлора функцию y=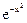 
, найти область сходимости ряда
Элементы гармонического анализа.
42. Является ли функция 
периодической?
43. Является ли функция 
периодической?
44. Найти период функции 
.
45. Написать закон гармонических колебаний с амплитудой 5, частотой 2 и начальной фазой 
.
46. Разложить в ряд Фурье функцию f(x) =1 при 0 
П и f(-x) = -f(x).
47. Разложить в ряд Фурье функцию y = 
на (-П,П)
48. Разложить функцию в ряд Фурье (при необходимости продолжив её периодически на всю числовую ось)
y=x -1, -2 <x 
2
49. Разложить функцию 
на промежутке (-П, П] в ряд Фурье, найти и построить амплитудный и фазовый спектры функции
50. Разложить функцию в ряд Фурье, построить амплитудный и фазовый спектры функции
f(x) =
-1 при x [-2;1)
x при x [-1; 1)
1 при x [1;2)
51. Представить интегралом Фурье функцию
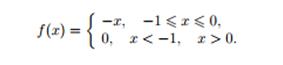
Основы вариационного анализа.*(самостоятельно)
52. Найти экстремали функционала, решив уравнение Эйлера.
Численные методы
53. Вычислить приближенно значение функции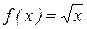 
в точке x=4.02.
54. Дана таблица значений функции
| N | ||||
| x | 0,1 | 0,3 | 0,6 | 0,8 |
| f(x) | 0,32 | 0,58 | 0,89 | 1,1 |
Написать интерполяционный многочлены Лагранжа, Ньютона.
Вычислить значение функции в точке 0,15 при помощи многочлена Ньютона и схемы Эйткена.
55. Вычислить 
с точностью 
=0,01.
56. Вычислить интеграл с точностью 
= 0,001, разложив подынтегральную функцию в ряд и почленно его проинтегрировав
57. Найти четыре первых (для ДУ II порядка три первых) отличных от нуля члена разложения искомого частного решения
, 
58. Провести отделение корней уравнения 
.
59. Найти корни уравнения 
методами половинного деления, хорд, касательных.
60. Вычислить интеграл 
по формулам Симпсона, трапеций, прямоугольников.
61. Методом Эйлера найти значение решения дифференциального уравнения 
для которого y( 1 )= 1, в пяти точках отрезка [1;2], приняв h= 0,2.
