Определение уравнения в полных дифференциалах
Дифференциальное уравнение вида
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u (x,y) с непрерывными частными производными, что справедливо выражение
Общее решение уравнения в полных дифференциалах определяется формулой
где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P (x,y) и Q (x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P (x,y) dx + Q (x,y) dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
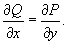
42) Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.
Обыкновенным дифференциальным уравнением n -го порядка называется уравнение вида
F (x, y, y ', y '',..., y (n)) = 0,
где F - известная функция (n +2) переменных, определенная в области DÌRn +2, x - независимая переменная из интервала (a, b), y = y (x) - неизвестная функция, n - порядок уравнения.
Уравнение
, (1)
где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области 
и во всяком случае зависит от 
, называется обыкновенным дифференциальным уравнением n -го порядка.
Рассмотрим некоторые типы уравнений высших порядков, допускающие понижение порядка.
Уравнения, не содержащие искомой функции и нескольких последовательных производных.
Рассмотрим уравнения вида
. (2)
С помощью замены 
, где u - новая неизвестная функция, уравнение (2) приводится к уравнению (n-k) -го порядка:
.
Уравнения, не содержащие явно независимой переменной.
Рассмотрим уравнения вида
. (3)
С помощью замены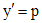 
(где p=p(y) - новая искомая функция независимая переменная) порядок уравнения (3) понижается на единицу, так как
,
,
..........................................................
.
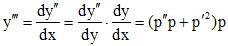Данная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:
.
При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения (3) решений такого вида.
43) Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
Линейным однородным уравнением 
-го порядка с постоянными коэффициентами называется уравнение вида
(1)
где коэффициенты 
– некоторые действительные числа. Для нахождения частных решении уравнения (1) составляют характеристическое уравнение
(2)
которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n степени и имеет n корней.
Тогда общее решение дифференциального уравнения (1) строится в зависимости от характера корней уравнения (2):
1.каждому действительному простому корню k в общем решении соответствует слагаемое вида 
;
2.каждому действительному корню кратности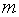 
в общем решении соответствует слагаемое вида 
;
3.каждой паре комплексных сопряженных простых корней 
и 
в общем решении соответствует слагаемое вида 
4.каждой паре комплексных сопряженных корней и 
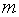кратности в общем решении соответствует слагаемое вида
51) Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора.
Ряд Тейлора
Основные разложения в ряд Тейлора
53) Ряд Лорана — двусторонне бесконечный степенной ряд по целым степеням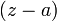 
, то есть ряд вида
Этот ряд понимается как сумма двух рядов:
1. 
— положительная часть ряда Лорана (иногда называется правильной) и
2. 
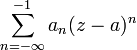— отрицательная часть ряда Лорана (иногда называется главной).
При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Область сходимости ряда по положительным степеням разложения функции в ряд есть сфера радиуса сходимости
. В области этой сферы лежит и область сходимости ряда по изолированному направлению делителей нуля. Если R=0, то ряд сходится только в точке a, если 
, то ряд сходится во всем пространстве Y.
Ряд по отрицательным степеням разложения функции сходится в сфере сходимости 
>r. Если r<R, то ряд сходится в области заключенной между двумя концентрическими сферами 
. На эту область накладывается область сходимости рядов по изолированному направлению. Сферы в пространстве это прежде всего поверхности 
, 
, натянутые без точек самопересечения на пространственные кривые 
, 
, эквивалентные кривым типа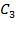 
. В области G, заключенной между двумя этими сферами, необходимо рассматривать область сходимости ряда по изолированному направлению, для точек 
.
50) Функциональные ряды в комплексной области
Понятия последовательности 
функций комплексной переменной (сокр. ФКП), ФР ФКП 
и его поточечной сходимости вводятся аналогично этим понятиям в действительной области. Область определения, область сходимости строятся на 
–плоскости.
Степенным рядом с комплексными членами называется ряд вида
где a0, a1, a2, …, an, - постоянные комплексные числа (коэффициенты ряда), z0 - фиксированное комплексное число (центр круга сходимости).
Теорема Абеля. Если степенной ряд сходится в точке z1 ≠ z0, то он абсолютно сходится в любой точке круга | z - z0| < | z1 - z0|;
Если этот ряд расходится в точке z2, то он расходится в любой точке z, удовлетворяющей неравенству | z - z0| > | z2 - z0| (т.е. находящейся дальше от точки z0, чем z2).
Из теоремы Абеля следует существование такого неотрицательного действительного числа R, что ряд абсолютно сходится в любой внутренней точке круга радиуса R с центром в точке z0, и расходится в любой точке вне этого круга. Число R называется радиусом сходимости, круг - кругом сходимости. В точках границы этого круга - окружности | z - z0| = R радиуса R с центром в точке z0 - ряд может и сходиться, и расходиться.
44) Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
Называется уравнение вида:
(1)
Где а1, а2, …, аn постоянные действительные числа.
Решение этого уравнения можно записать в виде:
Y= 
,
А частное решение можно найти с помощью метода вариаций.
Если правая часть имеет специальный вид, то частное решение можно найти методом “подбора”. Общий вид правой части уравнения (1) при котором можно применять метод подбора следующий:
F(x)=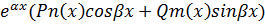 
, 
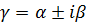
Где Pn и Qm многочлены.
Рассмотрим некоторые частные случаи:
1)F(x)=Pn(x), 
=0 если число совпадает с корнями характеристического ур-ния и S- число совпадений, то говорят что есть резонанс в степени S.
Если нет резонанса, то частное решение ищем в виде:
, где 
- многочлен n-ой степени с неопределёнными коэффициентами.
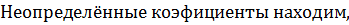представляя данное решение в исходное уравнение.
, то частное решение ищем в виде:
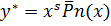
f(x)=Pn(x)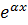 
, 
если нет резонанса:
f(x) = Pn(x)cos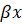 
+Qn(x)sin , 
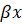Если нет резонанса, то:
cos +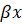 
, k=max[n,m];
( 
cos +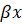 
;
Если правая часть представляет собой сумму выражений специального вида, то находим несколько частных решений и их складываем.
46) Функции комплексной переменной. Предел и непрерывность функции комплексной переменной.
Если каждой точке z = х + iy некоторого множества Е поставленно в соответствие одно или несколько комплексных чисел w = и + iv, то говорят, что на множестве Е определена функция (однозначная или многозначная) комплексного переменного w = f(z).
Функцию f(z) можно рассматривать как пару функций и{х,у) и v{x,y).
и{х,у) = Re/O + iу), v(x,y) = Imf(z + iy).
Предел и непрерывность функции комплексной переменной:
Число А называется 
ó(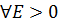
Функция f(z) называется неприрывной в точке z0, если предел f(z) z стремится к z0 =f(z0) 
.
