Подборка задач С2 из различных источников

В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой AB=13 и катетом BC=5. Найдите расстояние между ребрами AS и BC, если длина высоты SB равна 9.
В правильной треугольной пирамиде сторона основания равна 4, а боковое ребро 3. Найдите расстояние от стороны основания до противоположного бокового ребра.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине В и катетом АВ= . Найдите расстояние между ребрами SA и BC, если вершина пирамиды проектируется в середину ребра АВ и SA=
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С. Вершина S проектируется в точку В основания, причём боковые ребра пирамиды равны соответственно: AS=10, BS=7, CS=8. Найдите расстояние между ребрами AS и BC.
В правильной треугольной пирамиде боковое ребро равно 3 и отстоит от противоположного ребра основания на расстояние . Найдите длину стоны основания пирамиды, если она измеряется целым числом.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с катетом ВС=3 и гипотенузой АС=5. Расстояние между ребрами SA и BC равно 3. Найдите длину ребра SA, если вершина пирамиды проектируется в середину ребра АВ.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой АВ, равной 13 и катетом АС, равным 12. Вершина S пирамиды проектируется в точку В основания. Боковое ребро CS равно найдите расстояние между ребрами AS и BC.
В правильной треугольной пирамиде сторона основания равна 4 и находится на расстоянии от противоположного бокового ребра. Найдите длину бокового ребра.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с катетом ВС=3 и гипотенузой АС=5. Найдите расстояние между ребрами SA и BC, если вершина пирамиды проектируется в середину ребра АВ и SA=7.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой АВ, равной 12 и катетом ВС, равным 8. Вершина S пирамиды проектируется в точку В основания. Боковое ребро AS равно 13. Найдите расстояние между ребрами AS и ВС.
В правильной треугольной пирамиде сторона основания равна 3, а боковое ребро . Найдите расстояние от стороны основания до противоположного бокового ребра.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине В и катетом АВ=6. Найдите расстояние между ребрами SA и ВС если вершина пирамиды проектируется в середину ребра АВ, а высота пирамиды равна 4.
В основании прямой призмы АВСА В С лежит прямоугольный треугольник АВС с прямым углом С. Диагональ большей (по площади) боковой грани равна 20 и составляет с плоскостью основания угол 60 . Найдите угол между плоскостью АВ C и плоскостью основания призмы, если АС=6.
В основании прямой призмы АВСА В С лежит прямоугольный треугольник АВС с прямым углом С, катет АС в два раза больше катета ВС. Известно. Что плоскость AB C составляет с плоскостью основания угол 60°. Под каким углом диагональ большей (по площади) боковой грани наклонена к плоскости основания?
В правильной четырехугольной призме АВСDA B C D диагональ основания в 2 раза больше бокового ребра. Найдите угол между плоскостью АСВ и боковой гранью ВВ С С.
Основанием пирамиды служит квадрат, две боковые грани этой пирамиды перпендикулярны к плоскости ее основания, две другие ее боковые грани образуют с плоскостью основания равные двугранные углы, каждый из которых равен 30°. Высота пирамиды равна . Найдите площадь боковой поверхности пирамиды.
Диагональ основания правильной четырехугольной призмы равна 5 , а диагональ призмы наклонена к плоскости основания под углом 60°. Найдите площадь сечения призы, проходящего через сторону нижнего основания и противоположную сторону верхнего основания.
Основанием пирамиды является равнобедренная трапеция, большее основание которой равно 24, а боковая сторона равна 15. Основание высоты пирамиды, равной 8, лежит в центре окружности, вписанной в основание пирамиды. Найдите площадь боковой поверхности пирамиды.
Основание прямой четырехугольной призмы АBCDA B C D – прямоугольник ABCD, в котором АВ=12, AD= . Найдите квадрат косинуса угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD , если расстояние между АС и B D равно 5.
В правильной треугольной призме АВСА В С , все ребра которой равны 1, найдите косинус угла между прямыми АВ и ВС .
В кубе ABCDA B C D найдите квадрат тангенса угла между прямой АА и плоскостью ВС D.
В кубе ABCDA B C D найдите квадрат тангенса угла между прямой AC и плоскостью ВСС .
В правильной четырехугольной пирамиде SABCD все ребра которой равны 1, найдите косинус угла между прямой АВ и плоскостью SAD. В ответе укажите утроенное значение квадрата косинуса.
В правильной шестиугольной пирамиде SA…F, боковые ребра которой равны 2, а стороны основания - 1, найдите квадрат косинуса угла между прямой АС и плоскостью SAF.
В правильной прямоугольной призме АВСА В С все ребра которой равны 1, найдите квадрат косинуса угла между прямыми АВ и А С.
Основание прямой четырехугольной призмы ABCDA B C D – прямоугольник ABCD, в котором АВ=5, AD= . Найдите тангенс угла между плоскостью грани АА D D призмы и плоскостью, проходящей через середину ребра СD перпендикулярно прямой B D, если расстояние между прямыми А С и BD равно .
В правильной треугольной пирамиде SABC с основанием АВС известны ребра: АВ=8 , SC=17. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и ВС.
В правильной треугольной пирамиде SABC с основанием АВС известны ребра: АВ=20 , SC=29. Найдите угол, образованный плоскостью основания и прямой АМ, где М – точка пересечения медиан грани SBC.
В правильной треугольной пирамиде SABC с основанием АВС известны ребра: АВ=30 , SC=34. Найдите угол образованный плоскостью основания и прямой, проходящей через середины ребер AS и ВС.
В правильной треугольной пирамиде SABC с основанием АВС известны ребра: АВ=12 , SC=13. Найдите угол, образованный плоскостью основания и прямой АМ, где М – точка пересечения медиан грани SBC.
В прямоугольном параллелепипеде ABCDA B C D , у которого АВ=6, ВС=6, СС =4, найдите тангенс угла между плоскостями ACD и А В С .
В прямоугольном параллелепипеде ABCDA B C D , у которого АВ=4, ВС=6, СС =4, найдите тангенс угла между плоскостями CDD и BDA .
В кубе ABCDA B C D все ребра равны 1. Найдите расстояние от точки С до прямой BD .
В кубе ABCDA B C D все ребра равны 1. Найдите расстояние от точки С до прямой AD .
В прямоугольном параллелепипеде ABCDA B C D , у которого АА = 4, А D = 6, C D = 6, найдите тангенс угла между плоскостью АDD и прямой EF, проходящей через середины ребер АВ и В С .
В прямоугольном параллелепипеде ABCDA B C D , у которого АВ=4, ВС=6, CС =4, найдите тангенс угла между плоскостью АВС и прямой EF, проходящей через середины ребер АА и С D .
Дан куб ABCDA B C D . Длина ребра куба равна 1. Найдите расстояние от середины отрезка ВС до плоскости АВ D .
Дан куб ABCDA B C D . Найдите угол между плоскостями АВ D и АСD .
В правильной треугольной пирамиде SABC с основание АВС известны ребра: АВ=5 , SC=13. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и ВС.
Дан куб АВСDA B C D с ребром . Найдите расстояние от середины ребра А В до прямой МТ, где точки М и Т – середины ребер AD и CD соответственно.
Длины всех ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой ВМ и плоскостью BDP, если точка М – середина бокового ребра пирамиды АР.
Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми РН и ВМ, если отрезок РН – высота данной пирамиды, точка М – середина ее бокового ребра АР.
В прямоугольном параллелепипеде ABCDA B C D точка N - середина ребра CD, АВ=3, ВС=2, ВВ =2. Найдите угол между плоскостями АВ N и АВС.
В прямоугольном параллелепипеде ABCDA B C D точка М - середина ребра В C , АВ=3, ВС=4, ВВ =2. Найдите угол между плоскостями BMD и АВС.

45. В правильной треугольной пирамиде сторона основания равна 12см. Найдите расстояние от центра основания до боковой грани, если двугранный угол при ребре основания равен .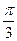

46. В правильной четырехугольной пирамиде двугранный угол при ребре основания равен 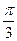. Найдите расстояние от стороны основания до противоположной боковой грани, если высота пирамиды 4см.

В правильном тетраэдре ABCD точка М середина ребра DC. Найдите угол между прямой ВМ и плоскостью АВС.
В правильной четырехугольной пирамиде SABCD все ребра равны 1. Точка М середина бокового ребра SC. Найдите угол между прямой ВМ и плоскостью основания.
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки. Е и F - середины ребер SB и SC соответственно. Найдите косинус угла между прямыми АЕ и BF.
В прямоугольном параллелепипеде ABCDA B C D , найдите угол между прямой АВ и плоскостью АА С, если АА =3, А В = 4, В С = 6.
В прямоугольном параллелепипеде ABCDA B C D , найдите угол между прямой ВС и плоскостью А ВС, если АА =12, АВ=6, ВС=5.
В прямоугольном параллелепипеде ABCDA B C D , найдите угол между прямой А D и плоскостью ВВ D, если DD =8, А D =6, D C =6.
В прямоугольном параллелепипеде ABCDA B C D , найдите угол между прямой А В и плоскостью АА С, если АА =6, АВ=8, ВС=8.