Линейная алгебра
1.1.1.
а) Очень простой пример. Умножь каждый элемент первой матрицы на 2, второй матрицы – на 3, затем найди разность полученных значений для каждого соответствующего элемента.
 =
= 
1.1.1. Это тоже простой пример. Но нудный.
Умножение матриц производится по формуле (см. http://ru.wikipedia.org/wiki/Умножение_матриц): 
Это значит в данном случае надо найти матрицу

 =
= 
где,
 =1*m+m*(-1)+(n+1)*3=3n+3
=1*m+m*(-1)+(n+1)*3=3n+3
 =…
=…
В общем, и так далее все 6 членов из сумм трех произведений.
1.2.1
Просто вычисли определитель по формуле:
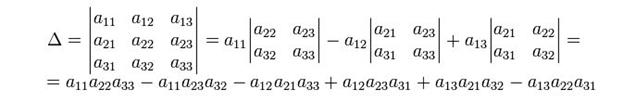
1.3.1. Для матрицы 2*2 формула совсем простая (http://ru.wikipedia.org/wiki/Обратная_матрица):

В твоем случае
 =
= 
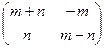 =
= 
1.4.2. Метод Гаусса описан здесь: http://ru.wikipedia.org/wiki/Метод_Гаусса
В твоем случае шаги такие:
1) умножаешь первое уравнение на m, второе – на 2. Находишь разность. Ставишь вместо второго уравнения. В нем отсутствует x1.
2) умножаешь первое уравнение на (m+n), третье – на 2. Находишь разность. Ставишь вместо третьего уравнения. В нем тоже отсутствует x1.
3) Точно также исключаешь x2 из третьего уравнения, находишь x3
4) Далее последовательной подстановкой находишь x1 и x2



Дальше аккуратно сокращаешь, что сокращается, и проводишь ту же операцию для исключения x2
3.2.1. Проще всего решать такие задачи, использую правило Лопиталя (http://ru.wikipedia.org/wiki/Правило_Лопиталя). То есть вместо функций в знаменатели и числители надо поставить их производные.
Пример (в) совсем прост. Сначала берется производная, снова получаем неопределенность 0/0

Второй раз берем производную:
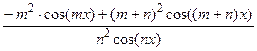
Здесь в точке 0 уже не неопределенности
Имеем

Пример (а) чуть сложнее. Правило Лопиталя применить затруднительно. Решение прикладываю.

Производные функции.
Вот здесь даны основные правила дифференцирования и таблица производных http://ru.wikipedia.org/wiki/Производная_функции, http://ru.wikipedia.org/wiki/Таблица_производных
Это достаточно просто.
Единственный пример, где надо сделать дополнительное действие – д. Там нужно сделать потенцирование-логарифмирование, чтобы вынести показатель степени в виде множителя. Это легко забыть, поэтому прикладываю решение.

Интегральное исчисление.
Таблица интегралов дана здесь http://ru.wikipedia.org/wiki/Таблица_интегралов
Пример (а) тривиальный. Просто представь радикал как степень (1/2)
Пример (в) – интегрирование по частям http://ru.wikipedia.org/wiki/Интегрирование_по_частям
Там тоже все просто. Посмотри сам.
4.2.1
Прикладываю решение:

Да, забыл arctg(1)=p/4, таким образом, окончательный ответ ln(p/2) - ln(p/4)= ln(2) = 0.693
Функции нескольких переменных
Частные производные находятся так же как и обычные, принимая вторую переменную как константу.
Я приводу фото решения для 5.11

и 5.1.2







