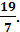1. Цифры трёхзначного числа образуют геометрическую прогрессию с разными членами. Если это число уменьшить на 200, то получится трёхзначное число, цифры которого образуют арифметическую прогрессию. Найдите первоначальное число. 842
2. Предприниматель купил акции компании First по цене 12 у.е. за акцию и компании Sekond по 9 у.е. за акцию, причём количество акций первой компании более чем на 5 превосходило количество акций второй компании, а общая стоимость была менее 390 у.е. Через некоторое время стоимость акции компании First возросла до 18 у.е за, а акции компании Sekond – до 21 у.е., и предприниматель продал акции более чем за 692 у.е. Определите количество акций каждой компании.
Ответ. 21 акция First и 15 акций Sekond
3. Купил Роман раков, вчера мелких, по цене 51 рубль за штуку, а сегодня – по 99, но очень крупных. Всего на раков он истратил 2520 рублей, из них переплаты из-за отсутствия сдачи в сумме составили от 16 до 20 рублей. Определить, сколько купил раков Роман вчера и сколько сегодня. Ответ: 18 вчера и 16 сегодня.
4. Папа Карло отправил Буратино в школу, дав ему на букварь несколько деревянных рублей, не более 30 штук. Буратино продал все рубли коллекционерам по 150 сольдо за каждый. Пять сольдо он сунул себе за щёку, не белее трёх закопал на поле Чудес, а на оставшиеся купил хлеба по цене 51 сольдо за корочку. Сколько корочек хлеба купил Буратино? 44
5. Сколькими нулями оканчивается число (200!)? 49
6. Найдите сумму всех трёхзначных чисел, не делящихся на 7
и оканчивающихся цифрой 3. Ответ: 42131
7. Чему равен наибольший делитель числа 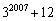 , не равный самому числу?
, не равный самому числу? 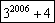
8. Натуральное число n при делении на 5 и на 29 даёт в остатке 1, а при делении на 27 и на 36 даёт в остатке 4. Найдите наименьшее возможное значение n. 436
9. При каких целых значениях k число 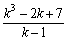 является
является
натуральным? Ответ: -5, -2, 2, 3, 4, 7.
10. Решить уравнение 4х3 – 20x2 + 13х + 12 = 0 х Î {-1/2, 3/2, 4}
11. Решить уравнение x4 + 2x3 – x – 2 = 0 х Î {1, -2}
12. Решить уравнение x5 + 2x4 + 2x3 – 2x2 – 3x = 0 х Î {-1, 0, 1}
13. Найдите наименьшее положительное значение параметра а, при котором уравнение 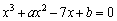 с целыми коэффициентами имеет три различных корня, один из которых равен 5. 14
с целыми коэффициентами имеет три различных корня, один из которых равен 5. 14
14. Определить, при каких значениях a и b полином x3 + ax2 + 2x + b
делится на полином x2 + x + 1. Ответ: a = 2, b = 1.
15. Найти все вещественные значения а, при каждом из которых числа
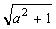 и
и 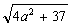 оба целые. Ответ:
оба целые. Ответ: 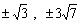
16. Решить в целых числах уравнение 2x2 – y2 – xy + x + 2y – 6 = 0.
Ответ: (2, 2), (2, -2), (-2, 0), (-2, 4) – всего четыре решения
17. Решить в целых числах уравнение |2m – 3| + |2 – n| = 5
Ответ: (1, -2), (1, 6), (2, -2), (2, 6), (0, 0), (3, 0), (0, 4), (3, 4),
(-1, 2), (4, 2)
18. Решить в целых числах уравнение m2 + 23 = n2
Ответ: (11, 12), (-11, -12), (11, -12), (-11, 12)
19. При каких значениях параметра а уравнение
2(a – 2)x2 + a(a + 1)x + 6 = 0 имеет только целые корни.
Ответ: а Î { -1, 2 }
20. Парабола 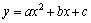 проходит через точки (2002, -32) и (m, 0).
проходит через точки (2002, -32) и (m, 0).
Найдите значение m, если известно, что a, b, m - целые числа,
причём m нечётно и меньше 2002. 2001
21. Найти все пары натуральных чисел (m, n), удовлетворяющие одновременно двум неравенствам 2m + 47 < 22n – 2n2 , 4n ³ 7m + 14.
Ответ: (1, 6), (1, 7), (2, 7)
22. Про семь натуральных чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из данных семи чисел делится на 5.
23. Cовокупность А состоит из различных натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел из А равно 210. Для любых двух чисел из А их наибольший общий делитель больше единицы. Произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа. Найти числа, из которых состоит А.
Ответ: А = { 6, 10, 14, 30, 42, 70, 105, 210 }
24. (С6 ЕГЭ 2010). Найдите все натуральные числа, которые делятся на 42 и имеют ровно 42 различных натуральных делителя (включая единицу и само число).
Ответ: 1) 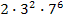 ,
, 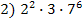 ,
, 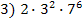 , 4)
, 4) 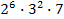 ,
,
5) 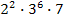 , 6)
, 6) 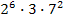 .
.
25. (Задание С6 ЕГЭ 2010). Среди обыкновенных дробей с положительными знаменателями, расположенными между числами 96/35 и 97/36, найдите такую, знаменатель которой минимален.
Ответ: 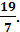
ОТВЕТЫ
1. 842
2. 21 акция First и 15 акций Sekond
3. 18 вчера и 16 сегодня.
4. 44
5. 49
6. 42131
7. 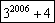
8. 436
9. -5, -2, 2, 3, 4, 7.
10. х Î {-1/2, 3/2, 4}
11. х Î {1, -2}
12. х Î {-1, 0, 1}
13. 14
14. a = 2, b = 1.
15. 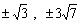
16. (2, 2), (2, -2), (-2, 0), (-2, 4) – всего четыре решения
17. (1, -2), (1, 6), (2, -2), (2, 6), (0, 0), (3, 0), (0, 4), (3, 4),
(-1, 2), (4, 2)
18. (11, 12), (-11, -12), (11, -12), (-11, 12)
19. а Î { -1, 2 }
20. 2001
21. (1, 6), (1, 7), (2, 7)
22.
23. А = { 6, 10, 14, 30, 42, 70, 105, 210 }
24. 1) 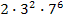 ,
, 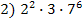 ,
, 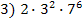 , 4)
, 4) 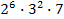 ,
,
5) 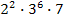 , 6)
, 6) 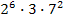 .
.
25.