Основная теорема алгебры. Всякий полином (многочлен)
разлагается на линейные и неприводимые квадратные множители в степенях, равных кратности корней.
Теорема Безу. Если число 
является корнем полинома 
кратности 
, то полином разлагается на множители:
.
Следствие. Если уравнение 
с целыми коэффициентами имеет целые корни, то эти корни являются делителями свободного члена 
.
Пример 13. Разложить на множители многочлен 
.
Решение: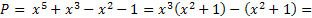 
.
Ответ: 
.
Пример 14. Решить уравнение x4 + 2x3 – 2x2 – 6x + 5 = 0.
Решение: Пользуясь следствием из теоремы Безу, целые корни ищем среди делителей числа 5. Корень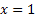 
подходит. Тогда из теоремы Безу следует, что многочлен делится на 
. Разложим на множители наш многочлен: 
Отсюда видно, что уравнение имеет единственный корень .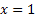
Ответ: .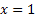
Пример 15. Найдите наибольшее значение параметра а, при котором уравнение 
с целыми коэффициентами имеет три различных корня, один из которых равен -2.
Решение: так как х = -2 – корень уравнения, то 
, откуда находим 
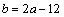. Поделив далее уравнение 
на (х + 2), получим: 
. Последнее уравнение с целыми коэффициентами должно иметь два различных решения, ни одно из которых не совпадает с -2. Так что имеем следующую систему условий:
Отсюда получаем, что наибольшим значением параметра а, при котором уравнение с целыми коэффициентами имеет три различных корня, один из которых равен -2, будет 
.
Ответ: 7
Решение уравнений в целых числах.
Пример 16. Решить в целых числах уравнение 
Решение: перепишем исходное уравнение в виде
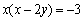
Так как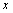 
и 
– целые числа, то возможны только следующие четыре случая:
1) 
2) 
3) 
4) 
Ответ: (1, 2), (-1, -2), (3, 2) и (-3, 2)
Пример 17. Решить в целых числах уравнение | m – 1| + |9 – 3n| = 7
Решение: Перепишем исходное уравнение в виде: 
.
Так как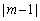 
и 
– целые неотрицательные числа, то возможны только следующие три случая:
1) 
2) 
3) 
Ответ: (0, 1), (0, 5), (2, 1), (2, 5), (-3, 2), (-3, 4), (5, 2), (5, 4), (-6, 3), (8, 3)
Пример 18. (Задание С6 ЕГЭ 2010). Решите в целых числах
уравнение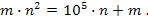 
Решение. Преобразуем уравнение к виду: 
. Отсюда следует, что m делится на т, т.е. 
. Если n четное, 
, то 
. Это уравнение не имеет решений, т.к. при делении на 4 левая часть имеет остаток (-1), а правая имеет остаток 1. Таким образом, n нечетное, т.е. 
. Тогда 
= 
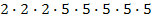. Среди делителей правой части только 2 последовательных числа: 4 и 5 или -5 и -4, т.е. 
или 
.
Ответ: 
или 
.
Разные задачи
Пример 19. Сколькими нулями оканчивается число (100!)?
Решение: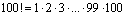 
. Заметим, что так как 
, то, если в разложении числа на простые множители окажется m «двоек» и n «пятёрок», то это число оканчивается k = min { m, n } «нулями». Очевидно, что в разложении на простые сомножители числа 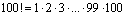«пятёрок» меньше, чем «двоек». Поэтому здесь k = n. Подсчитаем число «пятёрок». Из первых 100 натуральных чисел ровно 100: 5 = 20 чисел делится на 5, а из этих 100 чисел ровно 20: 5 = 4 числа делятся на 52, поэтому k = n = 25 + 4 = 29.
Ответ: 29
Пример 20. При каких значениях параметра а уравнение
ax2 + 3x + 2a2 = 0 имеет только целые корни.
Решение: Согласно теореме Виета, если у квадратного уравнения есть корни, то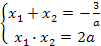 
, т.е. если 
. Если корни целые, то целыми будут и их сумма и их произведение, т.е., 
. Тогда 
. Подставляя эти значения в дискриминант, выбираем подходящие: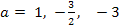 
. Кроме этого нужно рассмотреть случай, когда уравнение не является квадратным, т.е. при 
. В этом случае 
– целый корень.
Ответ: а Î { -3, -3/2, 0, 1 }
Пример 21. Найти все такие натуральные числа n, для которых из трёх следующих утверждений два будут верными, а одно – ложным:
1) n + 41 является квадратом натурального числа,
2) n – 21 делится без остатка на 10,
3) n – 48 является квадратом натурального числа.
Решение: Если число n – 21 делится без остатка на 10, то число 
оканчивается цифрой 1, и оба утверждения 1) и 3) ложны, так как квадрат натурального числа не может оканчиваться ни на 2 (как число
n + 41), ни на 3 (как число n – 48). Поэтому утверждение 2) ложно, а утверждения 1) и 3) – верны. Так что n + 41 = m2 и n – 48 = k2, где m и k – некоторые натуральные числа. Отсюда получаем, что m2– k2 =
= (m – k)(m + k) = 89. Так как 89 – простое число, то m – k = 1 и m + k = 89, так что m = 45, k = 44 и n = 1984.
Ответ: 1984.
Пример 22. Известно, что p, p+10, p+14 – простые числа.
Найдите p.
Решение: заметим, что р = 2 не подходит, а р = 3 – подходит. А при любом р > 3 одно из чисел p+10 и p+14 делится на 3. А именно, если р = 3к +1, то делится на 3 число р + 14, а если р = 3к + 2, то делится на 3 число р + 10.
Ответ: р = 3.
Пример 23. В магазине «Непарная обувь» за два дня продали 2 одинаковых правых сапога, 13 одинаковых левых сапог и один валенок, причём в первый день была выручена та же сумма, что и во второй. Левый сапог дешевле правого и дороже валенка на одну и ту же сумму. Сколько левых и сколько правых сапог продали в один день с валенком?
Решение: Пусть в один день с валенком продано 
правых и 
левых сапог. Тогда в другой день было продано 
и 
правых и левых сапог соответственно. Если с – цена левого сапога, и он на s дороже валенка, то цена правого сапога равна 
, а из условия задачи следует, что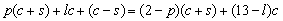 
,
то есть 
. Число p может принимать одно из трёх значений: 0, 1 или 2. При 
имеем: 
, и, кроме того, 0 < s < c. Поэтому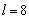 
. При 
имеем: 
, и, кроме того, 0 < s < c. Поэтому таких 
нет. При 
имеем: 
, и, кроме того, 0 < s < c. Поэтому таких 
нет.
Ответ: 8 левых сапог и ни одного правого.
Пример 24. В магазине «Мойдодыр» в продаже имеются стиральные порошки в пачках трёх сортов: обычный, необычный и превосходный. Сначала количественное соотношение по сортам было 3: 4: 6. В результате продаж и поставок со склада это соотношение изменилось и стало 2: 5: 8. Известно, что число пачек превосходного порошка возросло на 80%, а обычного порошка уменьшилось не более чем на 10 пачек. Сколько всего пачек порошка было в магазине сначала?
Решение: по условию задачи в магазине было 3n пачек обычного, 4n пачек необычного и 6n пачек превосходного порошка, так что всего было 13n пачек порошка, причём n – натуральное число. А стало в магазине 2m пачек обычного, 5m пачек необычного и 8m пачек превосходного порошка, причём m – также натуральное число. Для нахождения n и m имеем следующую систему условий:
Решая эту систему условий, получим:
Отсюда находим к = 1, n = 20 и 13n = 260.
Ответ: 260.
Пример 25. (Задание С6 ЕГЭ 2010). Все обыкновенные правильные несократимые дроби, числители и знаменатели которых двузначные числа, упорядочили по возрастанию. Между какими двумя последовательно расположенными дробями находится число 
?
Решение. Найдем такие дроби, что 
. Тогда 
. Чтобы дроби были наиболее близкими, нужно, чтобы знаменатели были как можно больше и при этом выполнялись равенства 
(наиболее близкие целые числа, удовлетворяющие нужным неравенствам. Перебором находим: 
Отсюда следует, что 
, а 
. Из неравенств 
находим, что 
.
Ответ: 
.
Пример 26. (Задание С6 ЕГЭ 2010). При каком наибольшем n найдется n семизначных чисел, являющихся последовательными членами одной геометрической прогрессии?
Решение: 
. 
, 
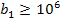. Отсюда имеем: 
.
Таким образом, 
. Чтобы членов прогрессии было как можно больше, ее знаменатель должен быть рациональным числом (т.к. все ее члены – целые числа), большим 1 и самым близким к 1, а именно 
Требуется найти такое p, при котором неравенство 
выполняется для наибольшего n. Для каждого n надо выяснить, какие степени соседних чисел обе будут семизначными числами. Путем несложных вычислений находим, что p = 4, n =11.
Ответ: 11.
Пример 27. (Задание С6 ЕГЭ 2010). На числовой оси отмечены все точки с целыми координатами. Разрешается прыгать на 1 и на 4 вправо или влево. Можно ли за 2010 таких прыжков попасть из точки 1 в точку 2, ни разу не попадая в точки с координатами, кратными 4?
Решение: Будем считать шаг вправо на 1 положительным, а влево – отрицательным. Положим, мы сделали p шагов на 1 клеточку вправо, l шагов на 1 клеточку влево, m шагов на 4 клеточки вправо и n шагов на 4 клеточки влево и из точки 1 попали в точку 2 за 2010 шагов. Тогда имеем систему А: 
. При этом числа 1+ p и 1+ p – l не должны делиться на 4, а их сумма при делении на 4 должна давать в остатке 2 (что следует из первого уравнения). Это возможно в следующих случаях: 1) 
, 2) 
, 3) 
, 4) 
. Подставим в систему А по очереди эти 4 случая.
1) 
Складывая и вычитая уравнения
системы, получим систему: 
. Теперь не трудно подобрать какие-нибудь значения параметров, удовлетворяющих системе. Например, 
тогда 
а тогда 
Ответ: можно.
Пример 28. Найти все целые корни уравнения 
Решение: 
Последнему условию делимости удовлетворяют только k = -2, 0 или -10. Но всем условиям удовлетворяют только k = -2, или -10. В первом случае х = -7, а во втором х = -31.
Ответ: x Î { -7, -31 }
