Неравенством с двумя переменными х и у называется неравенство вида
(или знак 
),
где 
– некоторое выражение с данными переменными.
Решением неравенства с двумя переменными называют упорядоченную пару чисел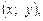 
при которой это неравенство обращается в верное числовое неравенство.
Решить неравенство – значит найти множество всех его решений. Решением неравенства с двумя переменными является некоторое множество точек координатной плоскости.
Основным методом решений данных неравенств является графический. Он заключается в том, что строят линии границ (если неравенство строгое, линии строят пунктиром). Уравнение границы получают, если в заданном неравенстве заменяют знак неравенства на знак равенства. Все линии в совокупности разбивают координатную плоскость на части. Искомое множество точек, которое соответствует заданному неравенству или системе неравенств, можно определить, если взять контрольную точку внутри каждой области.
Системы, содержащие неравенства с двумя переменными, вида
называются системами неравенств с двумя переменными. Решением данных систем является пересечение решений всех неравенств, входящих в систему.
Совокупность неравенств с двумя переменными имеет вид
Решением совокупности является объединение всех решений неравенств.
Пример 1. Решить систему 
Решение. Построим в системе Оху соответствующие линии (рис. 4.24):
 |
Рис. 4.24
Уравнение 
задает окружность с центром в точке О ¢(0; 1) и R = 2.
Уравнение 
определяет параболу с вершиной в точке О (0; 0).
Найдем решения каждого из неравенств, входящих в систему. Первому неравенству соответствует область внутри окружности и сама окружность (в справедливости этого убеждаемся, если подставим в неравенство координаты любой точки из этой области). Второму неравенству соответствует область, расположенная под параболой.
Решение системы – пересечение двух указанных областей (на рис. 4.24 показано наложением двух штриховок).
Задания
I уровень
1.1. Решите графически:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
II уровень
2.1. Решите графически:
1) 
2) 
3) 
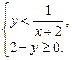
2.2. Найдите количество целочисленных решений системы:
1) 
2) 
3) 
2.3. Найдите все целочисленные решения системы:
1) 
2) 
3) 
2.4. Решите неравенство. В ответе укажите количество решений с двумя целочисленными координатами:
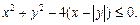
III уровень
3.1. Найдите количество целочисленных решений системы:
1) 
2) 
3.2. Найдите все значения параметра а, при каждом из которых система имеет решение:
1) 
2) 
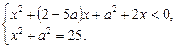
3.3. Определите, при каких значениях а неравенство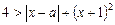 
имеет положительные решения.
3.4. Определите, при каких значениях а система имеет единственное решение:
1) 
2) 
3) 
3.5. В зависимости от значения а определите число решений системы
3.6. Решите графически:
1) 
2) 
