Цель работы: изучить особенности неразветвленной электрической цепи при различных соотношениях индуктивного и емкостного сопротивлений.
Схема замещения неразветвленной электрической цепи, содержащей индуктивную катушку и конденсатор представлена на рис.1.
Проанализируем данную электрическую цепь – рассмотрим значения тока цепи I, напряжения на отдельных участках UR, UL, UC, полной, активной, реактивной мощностей.
Так как при последовательном соединении элементов R, L, C ток является общим для всех элементов цепи, то удобно принять
i = Im sinωt.

Рис.1. Электрическая цепь с последовательным соединением R, L, C
По II Закону Кирхгофа
u = uR + uL + uC.
или
u = UmахR sinωt + UmахL sin(ωt + π/2) + UmахC sinωt(ωt - π/2) =
= UmахR sinωt + (UmахL - UmахC)sin(ωt + π - π/2) =
= UmахR sinωt + (UmaxL - UmaxC)sinωt(ωt + π/2).
Таким образом, полное напряжение цепи состоит из двух синусоидальных слагаемых одинаковой частоты, а, следовательно, являются так же синусоидальными с некоторой амплитудой Umах и фазовым углом φ (при условии, что начальная фаза тока равна 0).
u = Umах sin(ωt + φ).
Векторные диаграммы тока и напряжений цепи при различных соотношениях XL и XC показаны на рис.

Рис. Векторные диаграммы при различных соотношениях XL и XC:
а) XL > XC б) XL, < XC с) XL = XC
Из векторных диаграмм следует, что вектора напряжений образуют треугольник напряжений, в котором гипотенуза – входное напряжение цепи U, катет, прилегающий к углу φ - активная составляющая напряжения UR, второй катет UL – UC = UP – реактивная составляющая напряжения
UR = U cosφ; UP = U sinφ;
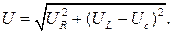
Если в треугольнике напряжений все стороны разделить на ток I, то получим треугольник сопротивлений (рис.), а если умножить на I2 – треугольник мощностей (рис.).

Рис. Треугольник мощностей Рис. Треугольник сопротивлений
Из треугольника сопротивлений
R = Z cosφ; X = Z sinφ; 
Из треугольника мощностей
P = S cosφ; Q = S sinφ; S = 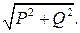
Из треугольников определяют
cosφ = UR/U = R/Z = P/S.
Свое название cosφ получил из треугольника мощностей – коэффициент мощности – важный показатель электрооборудования. Определяет, какую часть от полной мощности составляет активная мощность, мощность, расходуемая на совершение полезной работы.
Комплексные ток и напряжения:
İ = I e j 0.
 =
=  ej φ =
ej φ =  +
+  +
+  = I(R + I jXL - I jXC)= I (R + j (XL - XC)).
= I(R + I jXL - I jXC)= I (R + j (XL - XC)).
Разделив обе части уравнения на İ, получим комплексное сопротивление цепи:
Z = Uej φ /Iej 0 =Zej φ = R + j (XL – XC),
где Z =  модуль комплексного сопротивления, или полное сопротивление цепи;
модуль комплексного сопротивления, или полное сопротивление цепи;
R – активное сопротивление цепи;
XL – XC = Х -реактивное сопротивление цепи;
φ – аргумент комплексного сопротивления, равный углу сдвига фаз между векторами напряжения и тока
φ = arctg(XL – XC) /R.
При последовательном соединении элементов с R, L, C ток в цепи

В зависимости от соотношений между индуктивным и емкостным сопротивлениями в электрической цепи с последовательным соединением индуктивной катушки и конденсатора имеют место три характерных режима:
– режим недокомпенсации реактивного сопротивления, когда ток отстает от напряжения (XL>XC), 90°>φ>0;
─ режим, перекомпенсации реактивного сопротивления, когда ток опережает
напряжение (XC > XL), 0 < φ < – 90°;
– режим компенсации реактивного сопротивления, когда ток и напряжение совпадают по фазе (XC = XL), φ = 0°.
Из всех возможных соотношений между индуктивным XL и емкостным XС сопротивлений особый интерес представляет случай, когда эти сопротивления равны, т. е. ХL = ХС. В этом случае реактивное сопротивление X = XL – XC = 0 и полное сопротивление цепи Z = R минимально. Тогда ток в цепи I = U/R и при U = const, R = const значение его максимально.
Напряжения на индуктивном и емкостном элементах по значению
UL = XLI = XCI = UC.
Следовательно,
UL = XLI = XLU/R; UC = XCI = XCU/R.
Таким образом, напряжения на индуктивном и емкостном элементах могут превышать напряжение сети в XL/R раз, если XL>R.
Cдвиг по фазе между напряжениями UL иUC равен π, т.е. эти напряжения находятся в противофазе.
Такой режим цепи при последовательном соединении элементов с R, L и C, когда XL = XC, а напряжения на индуктивном (UL) и емкостном (UC) элементах, находящихся в название режима резонанса напряжений.
Векторная диаграмма напряжений для резонанса напряжений представлена на рис.. Реактивная составляющая напряжения равна нулю; следовательно, полное напряжение U = Uа, а угол сдвига фаз
φ = 0; cosφ = 1.
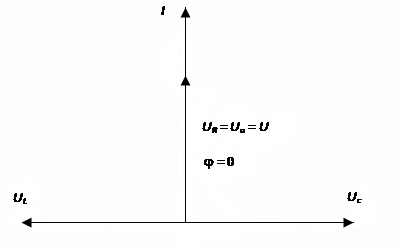
Рис. Векторная диаграмма для режима резонанса напряжений
Активная мощность такой цепи P = UI cosφ = UI = S, а реактивная
Q = UI sinφ = 0. В режиме резонанса напряжений реактивные мощности индуктивной катушки (QL = XLI 2) и конденсатора (QC = = XCI 2) равны между собой, но обратны по знаку. Происходит непрерывный обмен энергией между магнитным полем катушки и электрическим полем конденсатора.
Равенства индуктивного и емкостного сопротивлений ω L = 1/(ω C)
можно добиться, изменяя угловую частоту ω, индуктивность L или емкость С. Угловая частота, при которой наступает резонанс напряжений,
ω0 = 1/  .
.
При этой резонансной частоте, ток в цепи достигает максимального значения. При уменьшении частоты увеличивается сопротивление XC = 1/ (ω C), а следовательно, и реактивное сопротивление цепи X = XL – XC cтановится не равным нулю. Ток I =
= U /  уменьшается. При частоте ω = 0, что формально соответствует напряжению постоянного тока, ток в цепи равен нулю (XС = бесконечности) реактивное сопротивление цепи тоже становится больше нуля и ток начинает уменьшаться (рис.).
уменьшается. При частоте ω = 0, что формально соответствует напряжению постоянного тока, ток в цепи равен нулю (XС = бесконечности) реактивное сопротивление цепи тоже становится больше нуля и ток начинает уменьшаться (рис.).

Рис. Зависимость напряжений и тока от частоты 
Падение напряжения на элементе с активным сопротивлением
UR = RI изменяется так же, как ток в цепи, т. к. R = const. При этом UR = U при ω = ω0.
Явление резонанса напряжений используют в устройствах радиотехники, телевидения, автоматики и других электроустройствах.
Если электрическая цепь имеет такие L и С, что резонансной для этой цепи является частота ω0 =  , то ток этой частоты будет максимальным. Токи других частот (если в цепи действуют несколько напряжений разной частоты) будут меньше. Изменяя индуктивность L или емкость С можно настроить контур на эту частоту, т. е. усилить ток этой цепи.
, то ток этой частоты будет максимальным. Токи других частот (если в цепи действуют несколько напряжений разной частоты) будут меньше. Изменяя индуктивность L или емкость С можно настроить контур на эту частоту, т. е. усилить ток этой цепи.
В электросиловых устройствах это явление не нашло применения, так как в режиме резонанса напряжений резко увеличиваются напряжения UL и UC, что может привести к пробою их изоляции.
Домашнее задание по подготовке к лабораторному занятию:
– изучить материал, указанный в литературе;
– письменно ответить на контрольные вопросы.
– при заданных напряжении сети U, параметрах катушки Rk, Lk, частоте сети f = 50 Гц согласно номеру варианта (табл.) рассчитать емкость конденсатора С для получения резонанса напряжения в исследуемой цепи, рассчитать ток I рез. в этом режиме, а также напряжения на индуктивной катушке UL-R и конденсаторе UС. Полученные данные занести в табл..
Таблица
| Номер варианта | ||||||||
| U, В | 33,8 | 34,0 | 33,9 | 33,9 | 33,9 | 33,9 | ||
| Lк,мГн | ||||||||
| Rk, Ом | 55,4 | 45,9 | 76,5 | 84,7 | 38,1 | 47,5 | 38,2 | 38,0 |
Таблица
| C, мкФ | I рез, А | UL-R, В | UC, В | Примечание |
Подготовить бланк отчета к лабораторному занятию.
Порядок выполнения работы
1. Собрать электрическую схему согласно рис.

Рис.
2. После проверки схемы преподавателем подключить стенд к сети.
3. Увеличивая емкость конденсатора определить режим резонанса напряжения по показанию амперметра (максимальный ток). 
4. Увеличивая емкость конденсаторов, записать показания приборов в табл. для следующих режимов:
а) Xc >> XL, I A<< I рез
б) XC > XL, I A< I рез
в) XC  XL, I A = I рез
XL, I A = I рез
г) XC < XL, I A < I рез
д) XC << XL, I A<< I рез
Полученные данные внести в табл.
Таблица
| Измерено | Вычислено | |||||||||||||||
| U, В | UL-R,В | UC, В | I, А | Р, Вт | R, Ом | XL,, Ом | XC, Ом | Xр, Ом | Z, Ом | S, ВА | Q, вар | UR, В | UL, В | Up В | cosφ | φ, град |
5. По результатам исследования вычислить значения величин, приведенных в табл..
6. Построить векторные диаграммы тока и напряжений для пп.1, 3, 5; треугольники мощностей для п.п. 1, 5 табл.
При построении векторной диаграмм принять начальную фазу тока ψi равной начальной фазе напряжения по табл. согласно своему варианту.
7. Исследовать влияние изменения частоты сети, емкости конденсатора, индуктивности катушки на ток цепи и напряжения на реактивных элементах цепи, угол сдвига фаз, используя программу «SHABLON» (ауд.101,111 к.1):
– в программу 2 «Неразветвленные цепи синусоидального тока» ввести в базу данных из табл. значения напряжения U (В), индуктивности катушки L (мГн), из табл значение емкости конденсатора C, (мкФ); частоту сети f принять равным 50 Гц;
– набрав команду «Рассчитать», получить на экране значения:
UL – напряжение на катушке индуктивности
UC – напряжение на конденсаторе;
IT – ток цепи,
φ – сдвиг фаз
Получить графики зависимостей
I = f(f); UL = f(f); Uc = f(f); φ = f(f)
I = f(Lк); UL = f(Lк); Uc = f(Lк); φ = f(Lk)
I = f(C); UL = f(C); Uc = f(C); φ = f(C)
Проанализировать полученные зависимости.
8. Нанести на полученные графики экспериментальные значения I, Uc и расчетные величины I, UL, φ из табл.. Сравнить расчетные значения I рез., UC с экспериментальными данными табл.
9. Проанализировать результаты исследования.
10. Сформулировать выводы по работе согласно ее цели
Контрольные вопросы
1. В каких режимах может работать электрическая цепь при последовательном соединении R, L и C элементов?
2. Соотношение каких величин определяют режимы работы
электрических цепей?
3. Какое явление называется резонансом напряжения?
4. При каких условиях возникает резонанс напряжений?
5. Изменением каких параметров цепи можно добиться резонанса напряжений?
6. По показаниям каких приборов можно судить о наступлении резонанса напряжений?
7. Чему равен cosφ в режиме резонанса напряжений?
8. В каком соотношении могут быть величины входного напряжения и напряжений на реактивных элементах, содержащей R, L и С в режиме резонанса напряжений?
9. При каких условиях возникают перенапряжения на реактивных элементах цепи?
10. Где находит применение резонанс напряжений?
11. Почему не нашел применения резонанс напряжений в силовых цепях?
ЛАБОРАТОРНАЯ РАБОТА № 3
АНАЛИЗ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Цель работы: изучить особенности электрической цепи при различных соотношениях индуктивной и емкостной проводимостей; приобрести навыки настройки исследуемой цепи на различные режимы работы.
I. Общие сведения
При исследовании разветвленной цепи синусоидального тока, содержащей индуктивную катушку и конденсатор, её схема замещения может быть представлена параллельным соединением R – L, и С -элементами (см. рис. 10).
В процессе анализа данной цепи рассматриваются значение тока цепи I, протекающего по неразветвленному участку; токов I с ,IL-R, протекающих по параллельным ветвям цепи; полной, активной и реактивной мощностей (S, Р, Q) в зависмости от соотношений BL и BC.
Ток I, протекающий по неразветвленному участку цепи, согласно закону Ома для рассматриваемой цепи зависит от полной проводимости Y и приложенного напряжения U:
 ,
,
где Y - полная проводимость цепи:
 ;
;
где G – активная проводимость цепи, для рассматриваемой цепи  , См; BC, BL – соответственно емкостная и индуктивная проводимости цепи, См:
, См; BC, BL – соответственно емкостная и индуктивная проводимости цепи, См:
 ;
; 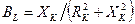 .
.
Согласно первому закону Кирхгофа, ток I связан с токами I с и IL-R уравнением  , или в комплексной форме записи
, или в комплексной форме записи  .
.
Векторная диаграмма цепи показана на рис.
На рис. вектора токов образуют треугольник, катеты которого равны активной Ia и реактивной IP составляющим тока, а гипотенуза – полному току I. Если IL > IC, то IP отстает по фазе от напряжения на угол π/2, а полный ток I – на φ (0 < φ < π/2). Если IL < IC, то ток IP опережает напряжение на угол φ, а полный ток I -на (-π/2 < φ < 0).
Если каждую сторону треугольника токов разделить на напряжение, то получим треугольник проводимостей, из которого следует, что полная проводимость цепи равна корню квадратному из суммы квадратов активной G и реактивной BР = BL – BC проводимостей.
Полный ток цепи при параллельном соединении элементов:
I = YU = 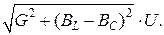

Рис. Треугольник токов Рис. Треугольник проводимостей
Из треугольника проводимостей получаем соотношения:
G = Y cosφ;
B = Y sinφ;
φ = arctg(B/G) = arctg((BL – BC) /G).
Полная проводимость цепи в комплексной форме
Y = 1 /Z = 1 /(Ze j φ) =Ye–j φ = G – jB,
где G и B – активная и реактивная проводимости соответственно.
Если в цепи преобладает индуктивная проводимость (ВL > ВC), то реактивная проводимость в комплексной форме отрицательна, а если преобладает емкостная проводимость (ВL < ВC), то – положительна.
В зависимости от соотношений между индуктивной и емкостной проводимостями в электрической цепи с параллельным соединением индуктивной катушки и конденсатора могут иметь место три характерных режима:
а) режим, при котором ток I отстает по фазе от приложенного к цепи напряжения U (BL>BC) этот режим называют режимом недокомпенсации реактивной мощности, на рис. 9а приведена векторная диаграмма токов и напряжений такой цепи;
б режим, при котором ток I опережает по фазе приложенное напряжение (BL<BC); этот режим называется перекомпенсацией реактивной мощности, векторная диаграмма то ков и напряжения приведена на рис. 9б;
в) режим совпадения по фазе тока I и напряжения U (BL=BC); векторная диаграмма токов и напряжений приведена на рис. 9в; этот режим электрической цепи называется резонансом токов.
Taк как режим резонанса токов возникает при  , то получить этот режим можно тремя способами:
, то получить этот режим можно тремя способами:
1. изменением ёмкости конденсатора C,
2. изменением индуктивности катушки L
3. или изменением частоты f приложенного напряжения U.
В режиме резонанса токов полная проводимостьцепи Y = G,так
как BL=BC, реактивная мощность равно нулю, а цепь потребляет
только активную мощность. Следовательно,cosφ = 1.
В режиме резонанса токов токи IL = IC и могут превышать общий ток I в цепи в BL/G раз, если BL = BC > G.
Векторная диаграмма для режима резонанса токов:

Рис. Векторная диаграмма для режима резонанса токов
Несмотря на то что в ветвях с L и C протекают токи, превышающие полный ток, эти токи всегда противоположны по фазе друг другу. Поэтому через каждую четверть периода происходит обмен энергией между магнитным полем индуктивной катушки и электрическим полем конденсатора, который поддерживается напряжением источника питания.
Режим резонанса токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты при заданных параметрах цепи. Графики зависимости тока в линии и коэффициента мощности от мощности конденсатора:
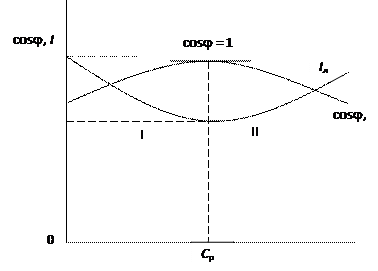
Рис. Зависимость тока в линии и коэффициента мощности от емкости
конденсаторов С; I – область недокомпенсации; II – область перекомпенсации
Резонанс токов нашел широкое применение в мероприятиях по повышению коэффициента мощности промышленных предприятий.
Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер: асинхронные двигатели, работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и др. Эти потребители работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность, что приводит к необоснованной загрузке реактивным током источников питания и линии электропередач.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею косинусных конденсаторов:

Электрическая цепь с параллельным включением конденсатора
Векторная диаграмма цепи:

Рис. Векторная диаграмма токов
На векторной диаграмме I л - полный ток, протекающий по линии электропередач до подключения батареи косинусных конденсаторов, I л1 – I л3 - после подключения батареи.
Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность установки, так как
Q = QL – QC,
и тем самым увеличивает коэффициент мощности.
Векторная диаграмма токов

Рис. 9.
При резонансе токов в электрической цепи:
а) полная проводимость равна активной проводимости, т.к. индуктивная и емкостная проводимости взаимно компенсируются;
б) в момент резонанса ток неразветвленного участка достигает минимального значения, т.к. полная проводимость цепи становится наименьшей, равной величине активной проводимости.
Резонанс токов широко применяется в электроустановках для компенсации реактивной мощности, во многих радиотехнических устройствах и т.д.
Домашнее задание по подготовке к лабораторному занятию
Изучить материал, указанный в литературе. По заданным параметрам катушки RK и LK и величине U согласно своему варианту (табл. 7) подобрать емкость конденсатора Срез для получения резонанса токов при частоте 50 Гц (см, рис. 10). Рассчитать Срез, Ic, IL-R, I. Полученные данные внести в табл. 8.
Таблица 7
| Вариант | ||||||||||
| LK, мГн | ||||||||||
| RK, Ом | 40,3 | 40,3 | 43,6 | |||||||
| U, В | 37,8 | 37,0 | 37,8 | 39,0 | 37,6 | 38,0 | 37,8 | 38,0 |
Таблица 8
Порядок выполнения работы
3.1. Собрать электрическую цепь согласно схеме на рис. 10.

3.2. Измерить напряжение питания схемы при помощи мультиметра.
3.3. Изменяя емкость, провести опыты для трех режимов:
а) BL>BC, когда IL-R>IC (2-3 измерения);
б) BL=BC, когда IL-R≈IC, I=Imin(1 измерение);
в) BL<BC, когда IL-R<IC (2-3 измерения);
3.4. Показания приборов записать в табл. 9.
Таблица 9
| № изм. | Измерено | Вычислено | ||||||||||||
| U, В | Iн, А | IL-R, А | IC, А | P, Вт | BL, См | BC, См | Y, См | C, мкФ | Ia, А | IL, А | Cos φ | Q, вар. | Φ, град. | |
3.5. По результатам исследования вычислить значения величин, приведенных в табл. 9, Указания о вычислении сопротивлений и мощностей см. в лабораторной работе № 1.
3.6. Построить векторные диаграммы токов и напряжения для трёх режимов работы (пп. 1,3,5 табл. 9),
3.7. Нанести на графики, построенные по распечаткам экспериментальные значения и расчетные величины из табл. 9. Сравнить расчетные значения с экспериментальными данными табл. 9 при резонансе.
3.8. Проанализировать результаты исследования и сформулировать выводы по работе.
Контрольные вопросы
1. Запишите законы Ома и Кирхгофа в комплексной форме для рассматриваемой цепи,
2. Начертите треугольники сопротивлений и проводимостей и выведите формулы перехода от сопротивлений к проводимостям и обратно.
3. Запишите условия наступления в цепи резонанса токов, выраженные через сопротивления параллельных ветвей.
4. Выведите формулу емкости, которая должна быть включена параллельно потребителю для повышения коэффициента мощности цепи. Начертите треугольник мощностей и запишите формулы для их расчета..
5. С помощью каких приборов и по каким признакам можно опытным путем определить наступление резонанса тока?
6.Укажите области применения резонанса токов.
1. Режимы работы цепи с параллельно соединенными R, L, C элементами: недокомпенсация, перекомпенсация, резонанс?
2. Написать единицу измерения проводимости. Физический смысл проводимости?
3. Записать условия резонансов токов через проводимости ветвей в разном виде.
4. Записать формулы ёмкости, которая подключена, параллельна нагрузки для cos j через tg.
5. Что показывают приборы в режиме резонансов токов?
6. Указать отличия резонансов токов от напряжения.
Формулы, используемые при расчётах:
 , где
, где  - полная проводимость цепи;
- полная проводимость цепи;  активная проводимость цепи;
активная проводимость цепи;  ,
,  - соответственно ёмкостная и индуктивная проводимости цепи.
- соответственно ёмкостная и индуктивная проводимости цепи.
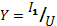



 , вар;
, вар;
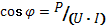 ;
;
ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ ЦЕПИ ТРЕХФАЗН0Г0 ТОКА ПРИ СОЕДИНЕНИИ ПРИЕМНИКОВ ПО СХЕМЕ «ЗВЕЗДА»
Цель работы: изучить влияние величины и характера нагрузки в одной из фаз приемника на фазное и линейное напряжения, напряжение смещения нейтрали в 3-проводной цепи и на ток в нейтральном проводе в 4-проводной цепи.
I. Обще сведения
Система трехфазного переменного электрического тока была предложена в конце 19 века. Благодаря работам Н. Теслы, Г. Феррариса и М.О. Доливо-Добровольского трехфазный ток быстро завоевал общее признание благодаря следующим достоинствам. Генераторы трехфазного тока, двигатели, использующие его энергию, - это наиболее совершенные, экономичные и надежные электрические машины, превосходящие по большинству технико-экономических показателей, как машины постоянного тока, так и машины однофазного переменного тока. Неоспоримы преимущества 3-фазного тока при передаче энергии на расстояние (исключая сверхмощные линии электропередачи протяженностью в несколько тысяч километров). В цепях 3-фазного тока путем несложных переключений можно подучить различные напряжения и мощности. Поэтому массовая электрификация промышленности началась, по существу, с появления 3-фазного тока.
Вообще m-фазной цепью называют совокупность электрических цепей, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые между собой по фазе на 2π/m. Для 3-фазиой цепи m=3, и сдвиг по фазе между ЭДС, приложенными к отдельным цепям, составляет 120° (2π/3).
Отдельные цепи, входящие в состав 3-фазной цепи, принято наливать фазами и маркировать буквами «А», «В», «С». Тогда, если принять  (т.е. начальная фаза ΨА=0), то
(т.е. начальная фаза ΨА=0), то  , а
, а 
В комплексном выражении  ;
;  ;
;  .
.
Безразлично какая из фаз будет принята за первую; важно только, что ЭДС следующей по порядку фазы от нее отстает, а ЭДС третьей фазы – опережает, При этом соблюдается порядок чередования фаз А–B–C (или В–С–А, или С–А–В).
Очевидно,  и
и  .
.
Приемники соединяются по схеме «звезда» в том случае когда их номинальное напряжение равно фазному напряжению источника. Соединение по схеме «звезда» - это такая схема при которой три конца фазных приемников (или фазных обмоток источника) соединяются в общую точку («нейтраль»), а три начала выводятся в линию. Естественно, понятия «начало» и «конец» являются условными и применяются только для определения направления ЭДС (или противоЭДС) в катушках. При отсутствии ЭДС (противоЭДС) маркировка начал и концов не имеет смысла.
На рис. 11 показано соединение по схеме «звезда» как источника, так и приемника энергии.
Рис.11
Ток, протекающий по фазе электроприемника, называется фазным, а ток в линейном проводе между источником и приемником – линейным,. На рис. 11 видно, что при соединении по схеме «звезда» цепь фазного тока  – это продолжение цепи линейного тока, т.е. линейный ток равен фазному.
– это продолжение цепи линейного тока, т.е. линейный ток равен фазному.
Напряжение между началом и концом фазы называется фазным, а между выводами разноименных фаз - линейным. Так, па рис. 11а фазные напряжения:  ,
,  ,
,  линейные (междуфазные) напряжения:
линейные (междуфазные) напряжения:  ,
,  ,
,  . Вобщем случае
. Вобщем случае  ,
, 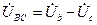 ,
,  , что непосредственно вытекает из рис. 11б.
, что непосредственно вытекает из рис. 11б.
При анализе 3-фазной цепи исходят из того, что источник всегда является симметричным ( ), а приемник может быть как симметричным, (
), а приемник может быть как симметричным, ( ), так и не симметричным. Очевидно, что при симметричном приемнике токи в фазах равны
), так и не симметричным. Очевидно, что при симметричном приемнике токи в фазах равны 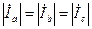 . В этом случае потенциалы нейтралей источника и приемника:
. В этом случае потенциалы нейтралей источника и приемника:  .
.
При соединении по схеме «звезда» несимметрия фазных нагрузок приводят к перераспределению потенциалов в цепи, между точками N и n появляется разность потенциалов, называемая смещением нейтрали 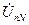 .
.
Рис.12
Как видно из рис. 12 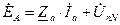 , т.е.
, т.е.

где  ,
, 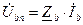 ,
,  .
.
В соответствий с методом узловых напряжений между узлами N и n

где  ,
,  ,
,  – комплексные проводимости фазных цепей.
– комплексные проводимости фазных цепей.
При симметричной нагрузке проводимости равны, и т.к
 ,
,  .
.
В этом случае
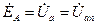 ,
,  ,
, 
(внутренним сопротивлением фаз источника и сопротивлением линейных проводов пренебрегаем): фазные напряжения на зажимах приемника образуют симметричную систему, они равны по величине и сдвинуты по фазе ровно на 120°. Поэтому
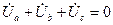 и
и  ;
;
Векторная диаграмма такой цепи показана на рис. 13:
 ;
;  .
.
Как и в однофазной цепи, угол φ определяется соотношением активного и реактивного сопротивлений в каждой фазе. Так,  и т.д.
и т.д.
Рис.13
Векторы линейных напряжений (UAB, UBC, UCA,) построены как геометрические разности соответствующих фазных. Нетрудно видеть, что п о модулю они больше фазных в  раз,
раз,
 .
.
При несимметричной нагрузке  , и хотя
, и хотя  , фазные напряжения
, фазные напряжения 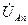 ,
,  ,
,  не равны между собой, существенно различаясь в зависимости от
не равны между собой, существенно различаясь в зависимости от  , что представляет серьезные неудобства для потребителей энергии, электрическое состояние такой цепи принято иллюстрировать топографической (потенциальной) векторной диаграммой, на плоскости которой координаты каждой точки соответствуют величине потенциалов изображаемых точек электрической цепи (рис. 14). В принятом масштабе расстояние между точками топографической диаграммы равно разности потенциалов (напряжению) между изображаемыми точками электрической цепи (например, цепи на рис. 11а).
, что представляет серьезные неудобства для потребителей энергии, электрическое состояние такой цепи принято иллюстрировать топографической (потенциальной) векторной диаграммой, на плоскости которой координаты каждой точки соответствуют величине потенциалов изображаемых точек электрической цепи (рис. 14). В принятом масштабе расстояние между точками топографической диаграммы равно разности потенциалов (напряжению) между изображаемыми точками электрической цепи (например, цепи на рис. 11а).
Точка N, изображающая нейтраль источника энергии, находится на рис. 14 в центре симметрии равностороннего треугольника линейных напряжений. Точка n, эквипотенциальная N в случае симметричной нагрузки, здесь смещается в соответствии с величиной и направлением вектора  . Векторы, соединяющие точку n с вершинами А, В, С, - фазные напряжения
. Векторы, соединяющие точку n с вершинами А, В, С, - фазные напряжения  ,
,  ,
,  . Здесь же построена векторная диаграмма токов в предположении активного характера нагрузки по фазам (
. Здесь же построена векторная диаграмма токов в предположении активного характера нагрузки по фазам ( ), По-прежнему
), По-прежнему
 , но
, но
 .
.
Преобразуя (5.1), можно показать что
 .
.
Существуют электроустановки с заведомо несимметричной нагрузкой (жилые дома, столовые, лаборатории, электросварочные участки и т.п.). Для того, чтобы обеспечить симметрию фазных напряжений в таких установках, нужно уравнять потенциалы нейтралей N и n, чтобы  . Это достигается прокладкой нейтрального (четвертого) провода в 3-фазной цепи между точками N и n (cм. рис. 11а).
. Это достигается прокладкой нейтрального (четвертого) провода в 3-фазной цепи между точками N и n (cм. рис. 11а).
Возникает переток зарядов по нейтральному проводу - ток 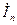 , причем, как видно из рис. 11а, по первому закону Кирхгофа:
, причем, как видно из рис. 11а, по первому закону Кирхгофа:
 . (5.2)
. (5.2)
Нельзя забывать о том, что уравнение (5.2) (как, впрочем, и все остальные) справедливо только в комплексном выражении.
При наличии нейтрального провода  , фазные напряжения становятся равны между собой, векторная диаграмма напряжений повторяет рис. 13, а на векторной диаграмме токов появляется ток
, фазные напряжения становятся равны между собой, векторная диаграмма напряжений повторяет рис. 13, а на векторной диаграмме токов появляется ток 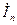 .
.
Мощность 3-фазной цепи складывается из мощностей отдельных фаз:
 .
.
В случае симметричной нагрузки

Если, как обычно, воспользоваться не фазными, а линейными значениями токов и напряжений, то при симметричной нагрузке
 .
.
Аналогичные выражения определяют реактивную и полную мощность 3-фазной цепи. Средневзвешенный коэффициент мощности
 .
.
Домашнее задание для подготовки к лабораторному занятию
2.1. Изучить материал по пособиям, указанным в перечне литературы.
2.2. Подготовить бланк отчета по лабораторному занятию.
2.3. По заданному линейному напряжению U=38 B и параметрам приемников согласно своему варианту по табл. 10 для цепи с нейтральным проводом рассчитать фазные и линейные напряжения и токи приемников, ток нейтрального провода, активные, реактивные и полные мощности. Полученные результаты записать в табл. 12.
Таблица 12
| Вариант | ||||||||||
 , Ом , Ом
| 40+J186 | -J300 | 43+J192 | -J300 | 40+J198 | -J90 | ||||
 , Ом , Ом
| 40+J188 | 19+J136 | -J300 | 40+J214 | -J300 | -J90 | 40+J45 | |||
 , Ом , Ом
| -J300 | -J300 | 84+J183 | -J300 | 43+J200 | -J300 | 84+J13 |
2.4, По результатам расчетов построить в масштабе векторную диаграмму напряжений и токов на комплексной плоскости. Полный расчет домашнего задания с векторной диаграммой приложить к отчету по лабораторной работе,






