Цель работы: получить навыки измерения и расчета сопротивлений и мощностей в цепи синусоидального тока; приобрести навыки сборки электрической схемы.
1. Общие сведения.
Схемы замещения элементов электрических цепей синусоидального тока (математические модели электрических цепей) составляются с помощью условных обозначений R –, L –, С – элементов. Параметры этих элементов:
- резистивный элемент с активным сопротивлением R, Ом, или активной проводимостью G = 1/R, Cм;
- индуктивный элемент с индуктивностью L, Гн, и реактивным индуктивным сопротивлением XL = 2πƒL, Ом или реактивной индуктивной проводимостью BL = 1/XL, См;
- емкостный элемент с емкостью С, Ф, и реактивным емкостным сопротивлением XC = 1/2 πƒC, Ом или реактивной емкостной проводимостью BC = 1/XC См.
Цепь с резистивным элементом.
Элементы электрической цепи, обладающие только активным сопротивлением R, называют резисторами (реостат, лампа накаливания). Пусть к зажимам цепи с активным сопротивлением R (рис.1) приложено напряжение
u = Umах sinω t.

Рис. 1. Электрическая цепь с резистивным элементом
В соответствии со вторым законом Кирхгофа для мгновенного значения напряжения u = Ri, т. е.

где Imах = Umах/R или I = U/R.
Из вышеприведенного видно, что вектора напряжения и тока в цепи с активным сопротивлением совпадают по фазе, что показано на векторной и временной диаграммах (рис. 2, рис.3).
Сдвиг по фазе между напряжением и током цепи равен
φ = ju - ji = 0° - 0° = 0°
Комплексные напряжение и ток цепи с резистивнымэлементом:
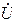 =
= 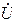 ej 0; φu = 0 °;
ej 0; φu = 0 °;
İ = Iej 0; φi = 0 °.
Тогда комплексное сопротивление цепи равно
Z =  /İ = Uej 0 /Ie j 0 = R,
/İ = Uej 0 /Ie j 0 = R,
т. е.комплексное сопротивление цепи с резистивным элементом равно положительному вещественному числу, модуль которого равен R
Векторная (на комплексной плоскости) и временные диаграммы приведены на рис. 2 и 3.


Рис. 2. Векторная диаграмма Рис. 3. Временная диаграмма
цепи с R-элементом цепи с R-элементом
Векторная диаграмма – это совокупность векторов, изображающих на плоскости синусоидально изменяющиеся с одной и той же частотой величины (напряжения, токи). Каждый вектор вычерчивается на комплексной плоскости с учетом его величины, начальной фазы, отсчитываемый от оси + 1.
Мощность цепи:
p = ui = U mахsinω tImах sinω t = UmахImах sin2ω t = UI (1 – cos2ω t),
т. к. напряжение и ток совпадают по фазе и мгновенное значение мощности всегда положительно. Таким образом, в цепи с резистивным элементом вся потребляемая электрическая энергия преобразуется в тепловую или другие виды энергии. Так как cosφ = 1, то среднее значение мощности за период равно активной мощности.
Р = UI = RI 2,
где Р – активная мощность цепи, Вт, кВт, мВт.
Полная мощность цепи с R -элементом равна активной мощности, которая характеризует интенсивность передачи электроэнергии от источника к приемнику и ее преобразование в другие виды энергии. Это активный необратимый процесс. Временная диаграмма мощности цепи приведена на рис.3.
В комплексной форме полная мощность:

 , ВА
, ВА
Активная мощность измеряется ваттметром РW = UI = RI2, ток – амперметром, а напряжение – вольтметром. Таким образом, активное сопротивление цепи, содержащей только резистивный элемент, можно определить по показаниям амперметра и вольтметра или по показаниям ваттметра и амперметра.
R = UR/I, P = PW.
Цепь с емкостным элементом.
Конденсатор – это элемент электрической цепи, обладающий емкостью. Конденсатор состоит из двух пластин с большой поверхностью, выполненных из проводникового материала и разделенных диэлектриком. Емкость конденсатора определяет тот электрический заряд, который накапливается на пластинах при разности потенциалов между ними в 1 В.
При подаче на конденсатор синусоидального напряжения в силу того, что напряжение непрерывно меняется по значению и направлению, меняется и заряд на пластинах конденсатора. Это изменение заряда и связанное с ним движение электронов и есть электрический ток в цепи.
Рассмотрим электрическую цепь, состоящую из источника питания и конденсатора емкостью С.

Рис. 4. Электрическая цепь с С-элементом
Пусть напряжение источника питания u = U махsinω t. Под действием напряжения в цепи возникает ток i и на каждой пластине конденсатора скапливается заряд Q = Cuc, где uс - падение напряжения на конденсаторе.
По второго закона Кирхгофа для цепи имеем u = uc.
Следовательно, ток в цепи, представляющий собой изменение заряда во времени равен:
i = dQ/dt = ω CUmах cosω t = ω CUmах sin(ωt + π/2) = I mахsin(ω t + π/2),
где амплитуда тока Imах = ω CU mах = Umах /(1/ω C).
Таким образом, в цепи с конденсатором ток опережает напряжение на угол π/2 и изменяется по синусоидальному закону.
Величина 1/ω C имеет размерность сопротивления, с/Ф = сВ/Кл = = сВ/сА = Ом). Это емкостное сопротивление
X с = 1/ω C = 1/2π fC = U c/ I
Емкостное сопротивление обратно пропорционально частоте и емкости конденсатора.
Комплексные напряжение и ток цепи
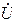 = Uej 0; ψ u = 0º;
= Uej 0; ψ u = 0º;
İ = Ie j 90; ψ i = + 90º;
Сдвиг по фазе между напряжением и током
φ = ψ u - ψ i = 0º - 90º = - 90º.
Комплексное сопротивление цепи
Z = 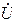 / İ = Uej 0/ Iej 90 = Хсe - j 90 = -jXс.
/ İ = Uej 0/ Iej 90 = Хсe - j 90 = -jXс.
Таким образом, комплексное сопротивление цепи с С- элементом равно отрицательному мнимому числу. Модуль комплексного сопротивления
Мощность цепи:
Р = ui = U mахsinω tI mахsin(ω t + 90°) = UI sin2ω t,
т. е. мгновенная мощность имеет только переменную составляющую. В первую и третью части периода, когда ток совпадает по направлению с напряжением, мощность положительна и энергия передается от источника питания к цепи, а во вторую и четвертую четверти периода энергия запасается в электрическом поле конденсатора.
Таким образом, через четверть периода мощность меняет знак. Такая энергия обмена энергией между источником и приемником, которая не преобразуется в другие виды энергии, называется реактивной. Интенсивность обмена энергией характеризуетсяреактивной мощностью Qс, равной амплитуде мгновенного значения мощности Qс = UI = - XсI2, где Qс – реактивная мощность цепи, вар, квар, мвар.
Полная мощность цепи с С -элементом равна реактивной мощности.
В комплексной форме полная мощность:
S =  = Sej φ = UI cos90° - jUI sin90° = - jUI, ВА
= Sej φ = UI cos90° - jUI sin90° = - jUI, ВА
Изменение мощности цепи с С -элементом, а также временные и векторная (на комплексной плоскости) диаграммы напряжения и тока представлены на рис. 5,6.
I 

Рис. 5. Временная диаграмма Рис.6. Векторная диаграмма
цепи с С-элементом цепи с С-элементом
В цепи с С - элементом ёмкостное сопротивление Хс и реактивная мощность Qc определяются по показаниям вольтметра Uc и амперметра Iа и равны:
Хс = Uc/ Iа,Ом; Qc = Uc Iа вар.
|
Трансформаторы, электрические двигатели, дроссели, кроме активного сопротивления обладают индуктивным сопротивлением. Индуктивностью обладают все проводники с током. В ряде случаев она мала и ею пренебрегают, но значительна там, где обмотки катушек состоят из большого числа витков провода.
Индуктивность возрастает, если магнитный поток замыкается по пути с малым магнитным сопротивлением (например, по стальному сердечнику).
Рассмотрим цепь с идеальной катушкой индуктивности с постоянной индуктивностью L, у которой активное сопротивление Rк = 0.

Рис. 7.Электрическая цепь с индуктивным элементом
Пусть к цепи с приложено напряжение u = U mахsinω t. Под действием напряжения в цепи возникает ток i, который создает магнитный поток Ф. Согласно закону электромагнитной индукции магнитный поток Ф индуцирует в катушке ЭДС самоиндукции
еL = - wd Ф /dt = - Ldi/dt,
где w - число витков катушки.
Знак «минус» согласно принципу электромагнитной индукции (закон Ленца) указывает на то, что еL всегда имеет такое направление, при котором она препятствует изменению магнитного потока или тока в цепи.
На рисунке показаны условные положительные направления напряжения u, тока i, ЭДС самоиндукции eL на элементе с индуктивностью L. Условное положительное направление ЭДС еL выбирают из условия, что ее действительное направление в любой момент времени противоположно напряжению на катушке uL.
По II ЗК имеем u - uL = 0, а с учетом того, что uL = - еL, получаем
u = eL = 0
Тогда
Umах sinω t – Ldi/dt = 0, или di/dt = Umах sinω t / L.
При решении этого уравнения получаем выражение для тока в цепи:
i = (Umах/L)sinω t d t = - Umах cosω t /ω L = Umах sin (ω t - π/2)/ω L =
= Imах sin(ω t - π/2).
Таким образом, в цепи с индуктивностью ток отстает от напряжения на угол π/2 и изменяется по синусоидальному закону.
Величина ω L имеет размерность сопротивления, Гн/с = В·с/А·с = = Ом.
Это индуктивное сопротивление XL = ω L = 2π fL.
Индуктивное сопротивление прямо пропорционально частоте и индуктивности. Тогда:
Imах = Umах/XL, или I = U /XL.
Так как ЭДС самоиндукции численно равна напряжению на элементе с индуктивностью, то XLI = U = ЕL
Следовательно, индуктивное сопротивление является коэффициентом пропорциональности между током i и ЭДС самоиндукции eL.
Комплексные напряжение и ток цепи
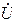 = Ue j 0, ψ u = 0o;
= Ue j 0, ψ u = 0o;
İ = Ie - j 90, ψ i = - 90o.
Сдвиг по фазе между напряжением и током
φ = 0° – (-90°) = +90o
Комплексное сопротивление цепи
Z = 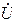 / İ = Ue j 0/ Ie - j 90 = XLej 90 = jXL.
/ İ = Ue j 0/ Ie - j 90 = XLej 90 = jXL.
Таким образом, комплексное сопротивление цепи с L -элементом равно положительному мнимому числу.
Модуль комплексного сопротивления
Z = XL
Мощность цепи с L -элементом:
р = ui = Umах sinω t - Imахsin(ωt - 90°) = - UIsin2ωt.
т. е. мгновенная мощность имеет только переменную составляющую. В первую и третью части периода ток направлен от цепи к источнику питания, а во вторую и четвертую – от источника питания к цепи. Таким образом, через четверть периода мощность меняет знак. Такая энергия обмена между источником и приемником, которая не преобразуется в другие виды энергии, называется реактивной. Интенсивность обмена энергией характеризуется реактивной мощностью QL = UI.
Реактивная мощность цепи QL = ULI = XLI 2, вар, квар, мвар.
Полная мощность цепи в комплексной форме:
S =  = Sej φ = UI cos90° + jUI sin90° = jUI, ВА
= Sej φ = UI cos90° + jUI sin90° = jUI, ВА
Временная и векторная (на комплексной плоскости) диаграммы цепи с идеальной индуктивностью а также изменение мощности представлены на рисунках 8 и 9.


Рис.8. Временная диаграмма Рис.9. Векторная диаграмма
Цепь с реальной индуктивной катушкой.
Схема замещения реальной индуктивной катушки содержит R и L – элементы (рис.9).

Рис.9. Схема цепи с R и L - элементами
Комплексное сопротивление цепи
Z экв = R + jX L = zejφ
φ = arctq XL / R
Ток цепи
İ =  / Z экв. .
/ Z экв. .
Напряжения участков цепи:
 = R İ; UL = jXL İ
= R İ; UL = jXL İ
Векторная диаграмма цепи с реальной индуктивной катушкой представлена на рис.10.
 İ
İ
Рис.10.Векторная диаграмма цепи с реальной индуктивной катушкой; ψi = 45º





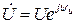 ,
,  . Комплексное сопротивление цепи
. Комплексное сопротивление цепи  , XL = 2 πƒL, R = 0, φ = arctg(XL/R) = 90˚, XL /0 = ∞, arctg ∞ = 90°. Ток цепи İL =
, XL = 2 πƒL, R = 0, φ = arctg(XL/R) = 90˚, XL /0 = ∞, arctg ∞ = 90°. Ток цепи İL = 
