Системы линейных алгебраических уравнений можно решать также, используя команду solve. Такое решение в силу простоты записи может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств, то есть с использованием фигурных скобок.
solve({eq1,eq2,…},{x1,x2,…})
Если для дальнейших вычислений необходимо использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name. Затем выполняется присвоения команда assign(name). После этого над решениями можно будет производить математические операции.
Решение систем из трех линейных уравнений имеет наглядную геометрическую интерпретацию – в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Это позволяет сделать функция импликативной графики implicitplot3d.
Формат:
implicitplot3d(expr1,x=a..b,y=c..d,z=p..q,<options>);
implicitplot3d(f,a..b,c..d,p..q,<options>);
где
f, expr1 – уравнение поверхности, которая должна быть построена;
a,b,c,d,p,q – пределы изменения соответствующих переменных;
options –параметры, с помощью которых можно в широких пределах управлять видом трехмерных графиков.
С помощью команды solve можно также решить систему неравенств. Например:
> solve({x+y>=2,x-2*y<=1,x-y>=0,x-2*y>=1},{x,y});

ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1
Построить графики трех функций sin(x),sin(x)/x, sin(x3/100) линиями трех цветов и трех типов.
> plot([sin(x),sin(x)/x, sin(x^3/100)],
x=10..10,color=[black,blue,red],style=[line,line,point]);
Результат представлен на рисунке 5.2.

Рис.5.2 – Графики трех функций
Задание 2
Построить поверхность h2 в цилиндрической системе координат.
> plot3d(h^2,a=-Pi..Pi,h=-5..5, coords=cylindrical, style=patch, color=sin(h));
Результат представлен на рисунке 5.3

Рис.5.3 – Пример трехмерного графика
Задание 3
Построить поверхности 2*sin(x*y), x^2+y^2-10, -x^2-y^2+10 в одной системе координат
> smartplot3d(2*sin(x*y),x^2+y^2-10,-x^2-y^2+10);
Результат представлен на рисунке 5.4.

Рис.5.4 – Поверхности, построенные в одной системе координат
Задание 4
Решить нелинейное уравнение вида y=2x2+1.25x-3.2. Выделить графически интервал изоляции корня уравнения и вычислить корень с точностью e = 10-5.
Сеанс работы с Maple:
> restart;
> fn:=2*x^2+1.25*x-3.2; # Определение функции через оператор присваивания

> plot(fn,x=-4..4,y=-5..15);# Графическое выделение интервала изоляции корня

> ans:=evalf(solve(fn,x),5);# Pешение уравнения и присвоение значений корней переменной ans
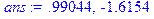
> x1=ans[1]; # Выделение первого корня уравнения

> x2:=ans[2]; # Выделение второго корня уравнения

> subs(x=ans[1],fn););# Подстановка первого корня в уравнение
> subs(x=ans[2],fn););# Подстановка второго корня в уравнение

Задание 5
Решить тригонометрическое уравнение вида y=sin(x2)+cos(x2). Выделить графически интервал изоляции корней уравнения на отрезке [-5..5] и вычислить все корни на этом отрезке.
Сеанс работы с Maple:
> restart;
> fn:=sin(x^2)+cos(x^2); # Определение функции через оператор присваивания
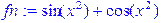
> plot(fn,x=-5..5); # Графическое выделение корней на заданном интервале

> ans:=solve(fn,x); #Pешение уравнения и присвоение значений корней переменной ans

> _EnvAllSolutions:=true;# Получение всех решений

> ans:=solve(fn,x);

> x1:=ans[1]; # Выделение первого корня уравнения

> x2:=ans[2]; # Выделение второго корня уравнения
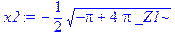
> x1*x2; # Действия над корнями

Задание 6
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте(Y)в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij). Исходные данные приведены в таблице 5.1.
Таблица 5.1. Исходные данные д ля межотраслевого баланса
| Отрасль-производитель Отрасль-потребитель | Коэффициенты прямых затрат | Конечный продукт, усл. ед. | ||
| 0,1 | 0,3 | 0,2 | ||
| 0,2 | 0,2 | 0,3 | ||
| 0,1 | 0,1 | 0,4 |
Как известно, матричная форма записи межотраслевого баланса имеет вид
X – AX = Y, (5.1)
где А – матрица коэффициентов прямых затрат;
Y– вектор конечного продукта;
Х – вектор объемов производства.
В натуральном балансе коэффициенты прямых затрат аij означают расход i-той продукции на изготовление единицы j-той продукции.
В стоимостном балансе коэффициенты аij означают затраты i-той отрасли на каждый рубль валовой продукции j-той отрасли.
Помножив вектор Х на единичную матрицу, соотношение (5.1) можно преобразовать как
ЕХ – АХ = Y (5.2)
или
(Е – А)X = Y. (5.3)
При известных значениях коэффициентов прямых затрат соотношение (5.3) можно использовать для анализа и планирования и решить следующие задачи:
· определить объемы валовой продукции отраслей X1, X2, …, Xn по заданным объемам конечной продукции по формуле
Х = (Е – А)-1Y; (5.4)
· определить объемы конечного продукта отраслей Y1, Y2, …, Yn по заданным объемам валовой продукции X1, X2, …, Xn по формуле
Y = (E – A)X. (5.5)
На основании вышесказанного по данным таблицы 5.1 можно записать следующую систему уравнений:
 X1 = 0.1X1 + 0.3X2 + 0.2X3 + 36
X1 = 0.1X1 + 0.3X2 + 0.2X3 + 36
X2 = 0.2X1 + 0.2X2 + 0.3X3 + 11
X3 = 0.1X1 + 0.1X2 + 0.47X3 + 8
Превратив конечные продукты отраслей в свободные члены, получим:
 X1 - 0.1X1 - 0.3X2 - 0.2X3 = 36
X1 - 0.1X1 - 0.3X2 - 0.2X3 = 36
X2 - 0.2X1 - 0.2X2 - 0.3X3 = 11
X3 - 0.1X1 - 0.1X2 - 0.4X3 = 8
Или
 0.9X1 - 0.3X2 - 0.2X3 = 36
0.9X1 - 0.3X2 - 0.2X3 = 36
- 0.2X1 + 0.8X2 - 0.3X3 = 11
- 0.1X1 - 0.1X2 + 0.6X3 = 8
Решение данной системы уравнений осуществляется известными методами линейной алгебры.
Найдем решение этой системы уравнений при помощи функции solve СКМ Maple.
Сеанс работы с Maple:
> sys:={0.9*x1-0.3*x2-0.2*x3=36,-0.2*x1+0.8*x2-0.3*x3=11,-0.1*x1-0.1*x2+0.6*x3=8}; # задание системы
уравнений

> ans:=solve(sys,{x1,x2,x3}); # присвоение переменной ans результатов решения системы
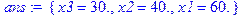
> subs(ans={x1,x2,x3},sys); # подстановка результата в уравнения системы
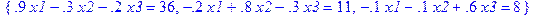
Таким образом, объемы валовой продукции отраслей X1, X2, X3 составят 60, 40 и 30 усл. ед. соответственно.
Задания для самостоятельной работы 
Задание 1. Решить нелинейное уравнение (см. таблицу 5.2). Выделить графически интервал изоляции корня уравнения, определить метод решения уравнения и вычислить корень с точностью e = 10-4.
Таблица 5.2
| Вариант | Уравнение | Вариант | Уравнение |
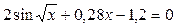
| 
| ||
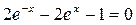
| 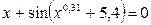
| ||
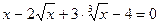
| 
| ||

| 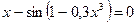
| ||
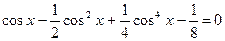
| 
| ||

| 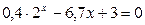
| ||
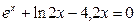
| 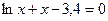
| ||

| 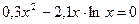
| ||

| 
| ||

| 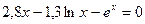
|
Задание 2. Решить неравенство (см. таблицу 5.3).
Таблица 5.3
| Вариант | Неравенство | Вариант | Неравенство |
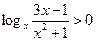
| 
| ||

| 
| ||

| 
| ||

| 9 | 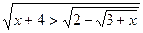
| |
| 5 | 
| 
|
Задание 3. Решить систему уравнений.
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
Предположив, что в прогнозном периоде конечный спрос на продукцию отраслей может измениться (Y1), определить темпы роста промышленного производства.
Вариант 1
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,1 | 0,3 | 0,4 | +20 | ||
| 0,2 | 0,2 | 0,5 | |||
| 0,2 | 0,2 | 0,1 |
Вариант 2
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,2 | 0,2 | 0,1 | |||
| 0,5 | 0,3 | 0,2 | +10 | ||
| 0,2 | 0,1 | 0,4 |
Вариант 3
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,3 | 0,4 | 0,2 | |||
| 0,2 | 0,1 | 0,3 | +25 | ||
| 0,1 | 0,5 | 0,2 |
Вариант 4
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,2 | 0,4 | 0,4 | |||
| 0,1 | 0,5 | 0,2 | |||
| 0,1 | 0,2 | 0,1 | +10 |
Вариант 5
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,1 | 0,4 | 0,5 | -5 | ||
| 0,1 | 0,5 | 0,4 | |||
| 0,2 | 0,2 | 0,1 |
Вариант 6
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,1 | 0,3 | 0,4 | +10 | ||
| 0,2 | 0,2 | 0,5 | |||
| 0,2 | 0,2 | 0,1 |
Вариант 7
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,3 | 0,1 | 0,1 | |||
| 0,4 | 0,3 | 0,5 | +5 | ||
| 0,5 | 0,2 | 0,1 |
Вариант 8
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,2 | 0,3 | 0,3 | |||
| 0,1 | 0,1 | 0,1 | |||
| 0,4 | 0,5 | 0,4 | +15 |
Вариант 9
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,1 | 0,5 | 0,4 | |||
| 0,2 | 0,2 | 0,1 | -10 | ||
| 0,2 | 0,4 | 0,4 |
Вариант 10
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % | ||
| 0,2 | 0,2 | 0,1 | -15 | ||
| 0,5 | 0,3 | 0,2 | |||
| 0,2 | 0,4 | 0,3 |
Задание 4. Решить систему неравенств (см. таблицу 5.4).
| Таблица 5.4. Вариант | Условие | Вариант | Условие |

| 
| ||

| 
| ||
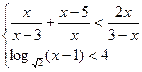
| 
| ||

| 
| ||
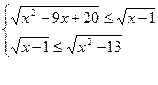
| 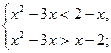
|
Задание 5. Построить поверхность (см. таблицу 5.5):
Таблица 5.5
| Вариант | Условие | Вариант | Условие |
| f = 2∙sin(xy), при x=-Pi..Pi, y=-Pi..Pi | f = Sin(x2+(y – 1)2) при x=-2..2, y=-1..3 | ||
| f = cos(x+y)-1 при x=-4..4, y=-4..4 | f=(exy)xy при x=-1..1,y=-1..1 | ||
| f = Cos(tx) ∙sin(ty) при x=-Pi..Pi, y=-Pi..Pi, t=1..4 | f = sin((x+2)t) при x=-10..10, t=1..20,n=1..50 | ||
| f = Sin(xy) при x=-Pi..Pi, y=-Pi..Pi | f=sin(x)×cos(x)×tan(x×y) при x=-4..4, y=-4..4 | ||
f=  при x = -10..10,
y = =-Pi..Pi, t=1..4
при x = -10..10,
y = =-Pi..Pi, t=1..4
| f =  при x=-4..4, y=-4..4
при x=-4..4, y=-4..4
|






