Решение уравнений и неравенств

Для решения уравнений, неравенств и их систем в СКМ Maple используется функция solve, которая возвращает последовательность решений.

Формат

solve(eqn, var);

 

где eqn – уравнение, неравенство или процедура;

var – имя переменной, относительно которой решается уравнение.

Уравнение и его решение можно представлять в виде отдельных объектов, отождествленных с определенной переменной. Например:

 

> ur:=x^2+2*x-3;# задание уравнения через переменную ur

> ot:=solve(ur,x);# решение уравнения и присвоение корней переменной ot

> x1:=ot[1];# присвоение первого корня переменной х1

> x2:=ot[2];# присвоение второго корня переменной х2

> subs(x=x1,ur);# подстановка первого корня в уравнение

> subs(x=x2,ur);# подстановка первого корня в уравнение

Если решений нет или функция не может найти решение, то возвращается пустая последовательность NULL. В этом случае целесообразно использовать функцию fsolve, которая возвращает корень уравнения в форме вещественного числа.

Формат

fsolve(eqn, var);

eqn – уравнение, неравенство или процедура;

var – имя переменной, относительно которой решается уравнение.

 

Например:

> solve(exp(x)+ln(2*x)-4.2*x);

 

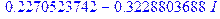
Как видно из результата решения данного уравнения, корень представлен с использованием мнимой единицы, что не дает представления о его числовом значении, поэтому для его решения следует воспользоваться командой fsolve.

> fsolve(exp(x)+ln(2*x)-4.2*x);

 

Классическим способом решения нелинейных уравнений является использование одного из численных методов. Подробнее с численными методами решения уравнений можно ознакомиться в [4].

Команда solve, примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале от 0 до 2*π. Например:

 

>solve(sin(x)=cos(x),x);

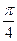
Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true. Например:

>_EnvAllSolutions:=true;

_EnvAllSolutions:=true;

>solve(sin(x)=cos(x),x);

В Maple символ _Z~ обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид , где n – целые числа.

Команда solve применяется также для решения неравенств. Решение неравенства выдается в виде интервала изменения искомой переменной. В том случае, если решение неравенства полуось, то в поле вывода появляется конструкция вида RealRange(– 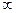, Open(a)), которая означает, что x (– 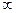, a), а – некоторое число. Слово Open означает, что интервал с открытой границей. Если этого слова нет, то соответствующая граница интервала включена во множество решений. Например:

> s:=solve(sqrt(x+3)<=sqrt(x-1)+sqrt(x-2),x);

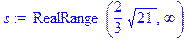
Если необходимо получить решение неравенства не в виде интервального множества типа x (a, b), а в виде ограничений для искомой переменной типа a<x, x<b, то переменную, относительно которой следует разрешить неравенство, следует указывать в фигурных скобках. Например:

> solve(1-1/2*ln(x)>2,{x});