Теория функций комплексного переменного
Производная функции комплексного переменного. Аналитичность. Степенной ряд, круг его сходимости. Ряд Тейлора.
Пусть f опред в обл Д, тогда произв в т.z. Пусть f опред в некот окр 
т. 
. Если сущ кон пред 
, то он назыв произв функ f в т. Z0 и об-ся 
. Из опред произв и св-в пред получ осн прав диф-я, аналог соотв-м прав диф-го исчисл ф-й действит перем.
Фун f, опред в окр т. 
, назыв аналит-ой в т. , если она диф-ма в нек окр этой т. Т.о. множ-во точек аналитичности ф-ии открыто. Ф-я, анал-я в кажд т.откр множ Д, наз аналитич в Д, или голоморфной, моногенной, правильной. Ф-я 
, назыв анал-ой в замкн обл 
, если сущ анал ф-я 
, так, что обл Д1 сод и 
для всех 
. Анал ф-я во всей пл-ти С назыв целой.
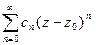-степ ряд. Ему можно пост в соотв рад R и круг с центр в т. рад R, U(z0,R) – круг сход-ти. R-рад сх-ти, U(0,R) –круг сх-ти.
Теор: Если ф-я f анал-я, то в окр произ т. 
, 
ф-я 
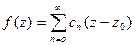, причём R ряда не меньше, чем 
, а коэф 
, где 
=окр с центр в т. , 
. Ряд 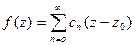назыв рядом Тейлора.
Интегральная теорема Коши. Разложение аналитической функции в ряд Тейлора. Интегральная формула Коши.
Т(Инт т Коши) Если G-односв обл в C и f –однозн анал в эт обл ф-я, то для люб замкн спрямляемой кривой L, леж в G, интегр от f вдоль L равен нулю: 
.
Здесь 
означ интегр по замкн конт L с обходом «против час стрел». Аналог утв-е (обобщ интегр теор Коши) им место и в том сл-е, когда G-внутрен-ть жордан-й спрямляемой кривой L, а f-ф-я, непрер в 
и аналит в G. Из этой теор след, что интегр от ф-и f, аналит-ой в односв обл G, завис только от нач и кон-й точек пути интегрир-я. Поэт для интегр вдоль спрямл-й кривой L, леж в обл G и соед точки z и z0, польз обознач 
, z z0-пред интегрир.
Инт ф-ла Коши: Пусть f(z)-однозн и анал в обл G ф-я, а L-замкнут жорд спрямляемая кривая, принадлеж G вместе со своей внутренностью D. Тогда для произв-й т. 
справ ф-ла: 
.
Инт-л, стоящ в прав части назыв инт-м Коши, след: 1)кажд анал ф-я в обл G бескон.число раз диф-ма в ней; 2) произ анал ф-ии в обл G сама явл ф-ей анал-ой в G; 3) действит и мним части анал ф-ии в G облад диф-ми част произв-ми всех пор-ов; 4) если L-замкнут жорд спрямл кривая, принадл G вместе со своей внутренностью D, а f(z)-анал в G, то для произвольной т. 
и люб натур k справ рав-во: 
.
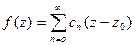Теор: Если ф-я f анал-я, то в окр произ т. , ф-я , причём R ряда не меньше, чем , а коэф , где =окр с центр в т. , .
Ряд Лорана. Особые точки. Вычет. Применения теории вычетов. Разложение аналитической функции в ряд Лорана.
Т(Лорана): Пусть f аналич в К, 
, тогда 
фун-ю f(z) можно предст в виде 
, где коэф. 
, n=…-2,-1,0,1,2…
Разлож фун назыв разлож Лорана, а ряд с коэф-ми, определ-ми по ф-ле назыв рядом Лорана в кольце К.
Будем говор, что т. явл-ся изолир-ой особой т,фун-и f(z), если найд-ся такая проколотая окр 
, в кот f(z) аналитич.
Классифик-я: 1) -устранимая особ т.фун f 
в разлож Лорана отсутствует главн часть: аn=0, n=-1,-2,…; 2) -полюс m-го поря-ка, если гл часть Лорана обрыв-ся на m-ом члене,т.е. 
3) -существенно особая т, если гл часть Лорана состоит из бескон числа членов.
Вычетом ф-ции f изолир особ т. Res f(z)=a1 назыв коэф с номером 
в разлож Лорана 
Вычет нах-ся раскладывая фунв окр т.в ряд Лорана.
Применение: 1) вычисл-ся интеграл в комп обл. 2) интеграл вида: 
, где функ-я R(u,v) явл-ся ф-ей 2-х переем-х; 3)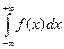 
, f(x) опред-ое на всей R представляет собой непрер сужение на эту ось функц f(x), кот явл-ся аналитич в пл-ти G, за исключ-м кон числа изолир особ точек z1,z2,…,zn.
