Третье основополагающее направление в теории состояний, далеких от равновесия, связано с анализом качественного поведения нелинейных динамических систем при изменении описывающих их параметров. Его основой является новая область математики — теория особенностей гладких отображений, сформировавшаяся на стыке топологии и математического анализа и получившая еще одно, более образное наименование — теория катастроф. В этой теории для анализа свойств систем дифференциальных уравнений уже не требуется предварительно находить полное множество решении. Дело в том, что для сложных систем знание всех точных решений избыточно: в реальных условиях они меняются за счет флуктуаций, и мы не получаем от этого знания нужной информации.
Первые результаты, связанные с качественным изучением поведения решений систем дифференциальных уравнений, были получены А. Пуанкаре и А. М. Ляпуновым почти 100 лет тому назад. Значительный вклад в развитие их идей внесли А. А. Андронов и Л. С. Понтрягин, которые ввели понятие грубости. т. е. структурной устойчивости системы. Но только с 50-х годов, после работ Р. Тома, началось интенсивное развитие как самой теории катастроф, так и ее многочисленных приложений.
Теория катастроф исследует динамические системы, составляющие широкий класс нелинейных систем и описываемые уравнениями вида:
где Xi — переменные, характеризующие состояние системы, Ca —набор параметров задачи (управляющие параметры). В элементарной теории катастроф рассматривается частный случай динамических систем: предполагается, что существует потенциальная функция—аналог потенциала электрического поля,
и что система находится в состоянии равновесия (Xi=0). Задача заключается в исследовании изменений состояний равновесия Xi(Ca) потенциальной функции U(Xi,Ca) при изменении управляющих параметров.
Элементарная теория катастроф является в известном смысле обобщением задач на минимум и максимум в математическом анализе. Для функции одной переменной ее поведение определяется невырожденными критическими точками — максимумами и минимумами. Эти точки соответствуют равенству нулю первой производной при второй производной, отличной от нуля. Сама функция в окрестности невырожденной критической точки может быть приведена к виду
подходящей гладкой (т. е. имеющей производные любого порядка) заменой переменных 
.
Аналогично в многомерном случае для критических точек, определяемых обращением в нуль первой производной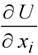 
и отличным от нуля аналогом второй производной, гессианом (детерминантом набора величии 
), существует гладкая замена переменных 
, в результате которой в окрестности невырожденной критической точки потенциальная функция приводится к квадратичной форме:
.
Эта форма может быть также преобразована, к виду 
.
Невырожденные критические точки определяют максимумы, минимумы и седловые точки различного типа и дают качественную картину поведения потенциальной функции в многомерном случае. Так, функция 
напоминает рельефную карту: вершины гор и седла связаны хребтами, имеются озерные впадины и седлообразные долины. Диагонализация 
дает направления славных осей линий максимального градиента. Если рельеф наполнить водой, то она соберется в озера, расположенные на дне долин. Минимум, который притягивает воду, называется аттрактором. Аттракторы разделяются седлами, хребтами, вершинами, образующими границу раздела между различными бассейнами притяжения. Типичная картина рельефа потенциальной функции, обладающей лишь невырожденными критическими точками, представлена на рис. 5.
Рассмотренная простая качественная картина многомерного рельефа существенно изменяется при наличии вырожденных критических точек, для которых одно или несколько собственных значений 
равно нулю. Равенство нулю 
возникает при некоторых определенных значениях управляющих параметров Ca. Если с изменением величин Ca система проходит через вырожденную критическую точку, то топография коренным образом меняется. Вместо знакомого пейзажа с хребтами и долинами возникает качественно новая картина, т. е. мы оказываемся как бы в совсем ином мире. И в этом смысле о переходе через особую точку говорят как о катастрофе. При приближении к границе перехода определенные критические точки рельефа сближаются, а затем сливаются.
Множество точек Ca, отвечающих функции с 
, разбивают пространство управляющих параметров на открытые области. Каждой из этих областей соответствуют качественно отличные рельефы. При пересечении границ, разделяющих эти области, — сепаратрисе, являющихся геометрическим местом особенностей, происходит качественное скачкообразное изменение — катастрофа состояний системы.
Рис. 5. Рельеф в пространстве переменных состоянии
Смысл развиваемого подхода состоит в нахождении вырожденных критических точек (поверхностей), соответствующих качественному изменению в топографии семейств потенциальных функций и выполнению вблизи них линейного анализа устойчивости.
В окрестности вырожденных, особых точек подходящим преобразованием координат потенциальная функция может быть представлена в виде:
.
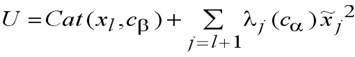l переменных, соответствующих нулевым собственным значениям матрицы Uij, являются аргументами функции катастрофы 
, зависящей также от B управляющих параметров. Зависимость потенциальной функции от остальных (n—l) переменных, соответствующих отличным от нуля собственным значениям, представляется, как и раньше, квадратичной формой.
Оказалось, что функции 
можно привести к определенному каноническому виду. Классификация особенностей потенциальных функций (катастроф) была проведена В. И. Арнольдом. Она удивительно совпала с классификацией таких как будто бы не имеющих ничего общего с особенностями объектов, как точечные группы первого рода, характеризующие симметрию молекул, а также оказалась связанной с правильными многогранниками в эвклидовым пространстве и простыми группами Ли. Причины этих связей еще не поняты до конца.
Для одной или двух переменных и числа управляющих параметров, не превышающего 5, имеется 7 типов элементарных катастроф. Для каждого типа катастроф рассматривается поверхность, зависящая от nj переменных состояния и na управляющих параметров в пространстве ni+na измерений. Поверхность простейшей катастрофы с одной переменной состояния и одним управляющим параметром приведена на рис. 6, а. Она имеет вид складки на ткани и называется катастрофой складки. Функция катастрофы в этом случае задается канонической формой 
. Соответствующие кривые для фиксированных значений параметра с приведены на рис. 6, б. При с >0 все кривые качественно подобны — они не имеют критических точек. Все кривые с с <0 также подобны и имеют две критические точки (рис. 6, б). Точка с =0 в пространстве управляющих параметров является сепратриссой (рис. 6, в). Катастрофы складки появляются в моделях, описывающих релаксационные колебания, триггерные схемы, нагруженные арки, различные диссипативные структуры.
Функция катастрофы сборки 
зависит от одной переменной состояния и двух управляющих параметров.
Рис. 7. Катастрофа сборки. Плоскость управляющих параметров
На рис. 7 показана сепаратрисса катастрофы сборки. Она разделяет плоскость управляющих параметров на две открытые области, представляющие функции с одной и тремя критическими точками. Линии сепаратриссы имеют дважды вырожденные точки, а точка пересечения — трижды вырождена. На рис. 7 изображены также потенциальные функции, соответствующие некоторым точкам плоскости управляющих параметров.
Модели, содержащие катастрофу типа сборки, используются в механике конструкций, при описании ряда колебательных режимов, в динамике квантовых систем. Аналогично, хотя и несколько более громоздко, выглядит описание остальных пяти типов элементарных катастроф.
Значение элементарной теории катастроф состоит в том, что она сводит огромное многообразие ситуаций, встречающихся на практике, к небольшому числу стандартных схем, которые можно детально исследовать раз и навсегда.
Математические образы теории катастроф овеществляются в волновых полях. Это так называемые каустики — геометрические места точек, в которых происходит заметная концентрация (фокусировка) волнового поля. Она может быть зарегистрирована физическими приборами или обнаружена визуально. С геометрической точки зрения каустики определяются как особенности некоторых отображений, осуществляемых семейством лучей. В геометрической оптике скачкообразное изменение состояния при пересечении каустики выражается в изменении числа лучей, приходящих в данную точку пространства. Все 7 канонических катастроф имеют свои образы в каустиках.
Сейчас теория катастроф широко применяется в ме-ханике конструкций, метеорологии, аэродинамике, оптике, теории кооперативных явлений, квантовой динамике. Но главное заключается в том, что эта теория подводит эффективную стандартную базу под описание качественных изменений в нелинейных уравнениях, моделирующих системы, далекие от равновесия. Она является основой анализа в теории бифуркаций, в теории переходов термодинамических систем в новые структурные состояния.
Катастрофы в природе
Планеты вселенной имеют пределы своего существования. Взрывы звёзд (по предложению Фрица Цвики из Калифорнийского технологического института их назвали в 1934 году "сверхновыми") остаются одной из главных проблем астрофизики. В нашей галактике вспышки сверхновых наблюдаются раз в 100-200 лет. Яркость звезды увеличивается в сотни миллионов раз и её можно видеть на небе среди бела дня. Постепенно блеск уменьшается и на месте звезды остаётся туманное облако, с трудом различимое в телескоп. Взрыв последней сверхновой зарегистрирован в феврале 1987 года. Результаты наблюдений, проведенные в Институте астрофизики имени Макса Планка (Гарчинг, Германия), показали, что вспышки сверхновых похожи на гигантские ядерные бомбы. При этом сам взрыв оказывается асимметричным, когда цепная ядерная реакция стремительно распространяется из глубины ядра направленно в одну сторону. В эту же сторону вытекают остатки звезды. Турбулентность увеличивает поверхность горения и скорость сжигания топлива. Ядерное горение распространяется со сверхзвуковой скоростью в виде ударной волны, разрывая звезду на части. Неизвестными остаются причины взрыва ядра. Многие исследователи называют причиной катастрофы гравитационный коллапс без описания его механизма. На нашей планете человечество вошло в период расцвета цивилизации, который характеризуется, кроме ряда достоинств развития, возможностью её гибели от действия самих людей. Поэтому вызывают определённый интерес условия существования планет и факторы возможных их катастрофических разрушений.
Жизнедеятельность структурных образований в природе обеспечивается системой их сохранения. Такой системой в межпланетном пространстве является гравитация.
Известно, что гравитационные силы самые универсальные среди всех сил природы. Любая форма, любой вид материи должны испытывать гравитационные воздействия. Исключение не составляет даже свет. Для всемирного тяготения нет преград. Действие сил простирается, непрерывно убывая, на неограниченные расстояния. Они вездесущи и всепроникающи. Все тела под действием одного только притяжения падают с одинаковым ускорением. Гравитационные силы долгое время назывались дальнодействующими, то есть действующими на расстоянии без каких бы то ни было посредников. Так считали, но примириться с этим не могли. Поиски посредника при гравитационных взаимодействиях начались одновременно с появлением в науке первых догадок об этих силах. Совершенно ясно понимал всю глубину физической проблемы и сам Ньютон. В письме к Бентли он писал: "Я считаю нелепостью допущение, будто тело, находящееся на некотором расстоянии от другого тела, может действовать на него через пустое пространство без всякого посредника. Поэтому тяжесть должна вызываться каким-то, действующим постоянно по определённым законам, агентом". Вопрос о природе этого агента остаётся открытым.
Законы механики Ньютона представлялись в то время способными описывать любое движение. При этом считали, что корнем всех явлений, основой, определяющей особенности движения, является сила. Принципы механики не могли "обойти" проблему гравитационного воздействия, не оказав на неё своего влияния. Закон всемирного тяготения был сформулирован по принципу механического взаимодействия: "Между двумя телами, находящимися на расстоянии, действует сила взаимного притяжения, пропорциональная произведению масс этих тел и обратно пропорциональная квадрату расстояния между ними". Такая формулировка закона оказалась серьёзным препятствием для понимания физической сущности гравитации. Гравитация, обладающая такими свойствами как универсальная, вездесущая и всепроникающая, должна характеризовать не взаимодействие между отдельными телами, а процесс обеспечения состояния определённых сложных структурных систем, влияния общего на частное. В материальном мире взаимодействия осуществляются не по правилам "демократии", декларируемым формулировкой закона всемирного тяготения, а по принципу подчинения частного общим. Наша планета подвержена гравитационному влиянию Солнечной системы, а та в свою очередь – нашей Галактики и так далее. К пониманию физической сущности гравитации можно прийти познав механизм и суть устойчивого, неиссякаемого, вихревого движения материи в природе.
Идея вихревого движения возникла в далёком прошлом. Ещё в семнадцатом веке возникло противостояние ньютонианского и картезианского направлений в естествознании. Теоретическим источником картезианства были идеи Р. Декарта (латинизированное имя – Картезий). Декарт явился автором теории, объясняющей образование и движение небесных тел вихревым движением частиц материи (вихри Декарта). С того времени произошли в науке такие фундаментальные сдвиги как возникновение понятия поля, создание электродинамики, теории относительности, квантовой механики. Появилась возможность рассмотреть идеи вихревого движения элементарных частиц на основе нового физического мировоззрения.
Заключение
Список литературы
1. http://katastrofa.h12.ru/theory
2. Публий Овидий Назон. Любовные элегии. Метаморфозы. Скорбные элегии Перевод с латинского С.В.Шервинского М., Художественная литература, 1983 OCR Бычков М.Н.
3.
