ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО (ФКП)
Комплексные числа и операции над ними
Комплексным числом 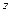 называется пара действительных чисел
называется пара действительных чисел 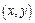 , записанных в определенном порядке:
, записанных в определенном порядке: 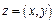 . Множество комплексных чисел будем обозначать
. Множество комплексных чисел будем обозначать 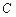 . Одним из обозначений служит запись вида
. Одним из обозначений служит запись вида
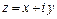 ,
,
называемая алгебраической формой записи комплексного числа 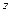 . В этой записи
. В этой записи 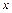 называется действительной,
называется действительной, 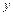 - мнимой частями комплексного числа
- мнимой частями комплексного числа 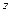 (для этого употребляется также запись
(для этого употребляется также запись 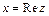 ,
, 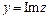 );
); 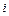 называется «мнимой единицей»:
называется «мнимой единицей»: 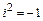 . Тригонометрическая форма записи комплексного числа имеет вид:
. Тригонометрическая форма записи комплексного числа имеет вид:
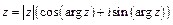 .
.
Здесь величина 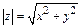 называется модулем комплексного числа; аргумент комплексного числа
называется модулем комплексного числа; аргумент комплексного числа 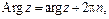
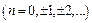 определяется из равенств
определяется из равенств  ,
, 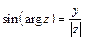 . Главное значение аргумента комплексного числа
. Главное значение аргумента комплексного числа 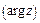 заключено в промежутке
заключено в промежутке 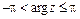 и вычисляется по формуле
и вычисляется по формуле
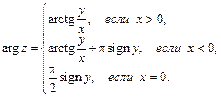
Показательная форма записи комплексного числа
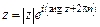 .
.
Арифметические действия над комплексными числами:
Равенство комплексных чисел 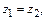 если
если 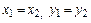 .
.
Сложение 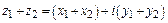 .
.
Вычитание 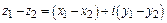 .
.
Умножение 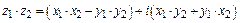 ,
,
в тригонометрической форме:
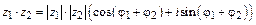 .
.
Деление 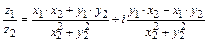 ,
, 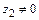 ,
,
в тригонометрической форме:
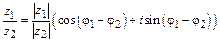 .
.
Сложение и умножение комплексных чисел подчиняются законам:
1. 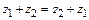 (коммутативность сложения);
(коммутативность сложения);
2. 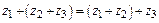 (ассоциативность сложения);
(ассоциативность сложения);
3. 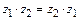 (коммутативность умножения);
(коммутативность умножения);
4. 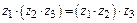 (ассоциативность умножения);
(ассоциативность умножения);
5. 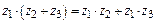 (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
Определение. Комплексное число 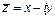 называется сопряженным комплексному числу
называется сопряженным комплексному числу 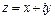 .
.
Свойства операции сопряжения:
1) 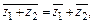 2)
2) 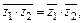
3) 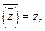 4)
4) 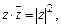 5)
5) 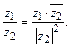
Вычисление корня из комплексного числа:
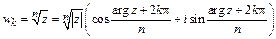 ,
,
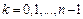 . Здесь
. Здесь 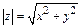 - модуль комплексного числа
- модуль комплексного числа 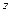 .Корни
.Корни 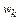 расположены на комплексной плоскости в вершинах правильного
расположены на комплексной плоскости в вершинах правильного 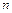 -угольника, вписанный в окружность радиуса
-угольника, вписанный в окружность радиуса 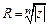 с центром в точке
с центром в точке 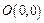 .
.
Возведение в степень. Формула Муавра.
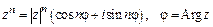 .
.
Элементарные функции комплексного переменного
Определение. В области 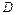 определена функция комплексного переменного
определена функция комплексного переменного 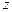 :
: 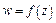 , если
, если 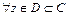 поставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений
поставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений 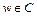 . Пусть
. Пусть 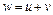 . Тогда
. Тогда
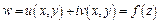 .
.
Функция комплексного переменного не имеет графика: она соответствует заданию двух действительных функций переменных 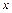 и
и 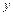 :
:
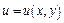 ,
, 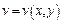 .
.
Геометрический смысл ее состоит в осуществлении отображения точек комплексной плоскости 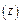 на соответствующие точки комплексной плоскости
на соответствующие точки комплексной плоскости 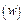 .
.
Показательная функция 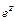 :
:
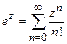
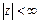 .
.
Тригонометрические функции 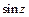 и
и 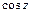 :
:

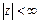 ;
;
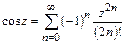
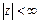 .
.
Справедливы формулы Эйлера:
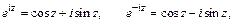
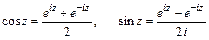 .
.
Тригонометрические функции 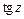 и
и 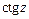 :
:
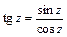 ;
; 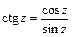 .
.
Гиперболические функции 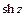 ,…,
,…, 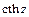 :
:
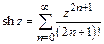 ;
; 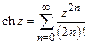 ;
;
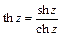 ;
; 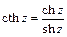 .
.
Имеют место соотношения:
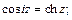
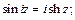
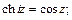
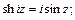
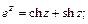
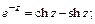
Логарифмическая функция 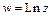
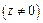 :
:
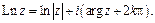
Обратные тригонометрические функции:
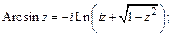
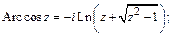
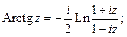
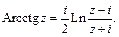
Обратные гиперболические функции:
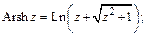
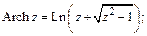
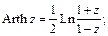
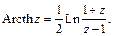
Общая степенная функция 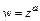 и общая показательная функция
и общая показательная функция 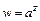 :
:
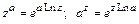
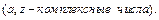
Дифференцирование ФКП. Аналитические функции
Определение. Однозначная функция 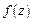 называется дифференцируемой в точке
называется дифференцируемой в точке 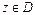 , если существует предел
, если существует предел
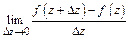 ,
, 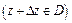 .
.
Этот предел называется производной функции 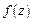 в точке
в точке 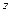 . Обозначается
. Обозначается 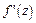 ,
, 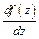 .
.
Теорема. Для того, чтобы функция 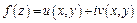 была дифференцируемой в точке
была дифференцируемой в точке 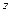 , необходимо и достаточно, чтобы функции
, необходимо и достаточно, чтобы функции 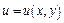 и
и 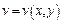 были дифференцируемы в этой точке и выполнялись условия Коши-Римана (д’Аламбера-Эйлера)
были дифференцируемы в этой точке и выполнялись условия Коши-Римана (д’Аламбера-Эйлера)
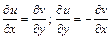 .
.
Определение. Функция 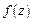 называется аналитической в данной точке
называется аналитической в данной точке 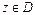 , если она дифференцируема как в самой точке
, если она дифференцируема как в самой точке 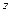 , так и в некоторой ее окрестности.
, так и в некоторой ее окрестности.
Определение. Функция 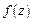 называется аналитической в области
называется аналитической в области 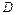 , если она аналитическая в каждой точке данной области.
, если она аналитическая в каждой точке данной области.
Формулы дифференцирования ФКП аналогичны соответствующим формулам дифференцирования функций действительной переменной.




