Первообразной для функции f(x) на
интервале (a, b) называется функция F (x), если:
F¢ (x) = f(x)
Первообразная функция F(x) для функции
f (x) = cos x равна:
sin x + C
Первообразная для функции
 равна:
равна:
tg x + C.
F(x) – одна из первообразных для функции
F(x). Тогда любая первообразная F(x) для
функции f (x) равна:
F(x) = F(x) + C;
Первообразная функция F(x) для функции
f (x) = x равна:
 ;
;
Соответствие первообразной F (x) функции f (x):
1-я пара:  ;
;
2-я пара:  ;
;
3-я пара:  ;
;
4-я пара:  ;
;
5-я пара:  ;
;
6-я пара: 
F(x) – первообразная для функции f(x). Тогда
неопределённым интегралом 
Называется
совокупность всех первообразных F(x) + C;
Frac34; дифференциал
Неопределённого
интеграла равен:
f(x)dx;
где F (x) – первообразная функции f (x).
F(x) – первообразная для функции f(x).
Тогда  равен:
равен:
f(x) + C;
где С – произвольная постоянная.
 равен:
равен:
С;
 равен:
равен:
х + С;
Соответствие неопределённых интегралов
функциям:
1-я пара:  ;
;
2-я пара:  ;
;
3-я пара:  ;
;
4-я пара:  ;
;
5-я пара:  ;
;
6-я пара:  .
.
Соответствие функций неопределённым
интегралам:
1-я пара:  ;
;
2-я пара:  ;
;
3-я пара: 
4-я пара:  ;
;
5-я пара  ;
;
6-я пара  .
.
Соответствие функций неопределённым
интегралам:
1-я пара:  :
:
2-я пара:  :
:
3-я пара: 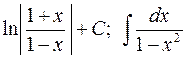 ;
;
4-я пара:  :
:
5-я пара:  ;
;
6-я пара:  .
.
 равен:
равен:
 ;
;
 равен:
равен:
 ;
;
 равен:
равен:
 ;
;
Сводится к табличному
заменой:
t = x2;
 равен:
равен:
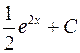 ;
;
Сводится к табличному
заменой:
t = lnx;
 равен:
равен:
 ;
;
 равен:
равен:
.  .
.
Соответствие функций неопределённым
интегралам:
1-я пара:  ;
;
2-я пара:  ;
;
3-я пара:  ;
;
4-я пара:  ;
;
5-я пара: 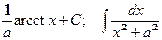 ;
;
6-я пара  .
.
Формула интегрирования по частям. ò udv
Равен
uv - òvdu;
Применить формулу интегрирования по
частям в интеграле ò x 2ln xdx при u =
lnx.
Применить формулу интегрирования по
частям в интеграле ò x 2cos 2 xdx при u =
x2;
ò xe - xdx равен:
. 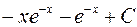 ;
;
òarctg xdx равен:
 ;
;
 равен:
равен:
ln| x ± a | + C;
 равен:
равен:
 ;
;
 равен:
равен:
. arctg(x + 1) + C;
 равен:
равен:
.  ;
;
 равен:
равен:
 ;
;
 равен:
равен:
 ;
;
 равен:
равен:
 ;
;
 равен:
равен:
ln| x2 - 4x + 5 | + 9arctg (x - 2) + C;
 равен:
равен:
 ;
;
Рациональная дробь (рациональная функции)
Pn(x), Qm(x) – многочлены степени
n и m) является правильной, если:
n < m;
 равен:
равен:
 .
.
 равен:
равен:
 ;
;
 равен:
равен:
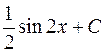 ;
;
 равен:
равен:
 .
.
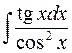 равен:
равен:
 .
.
 равен:
равен:
.  ;
;
 равен:
равен:
 .
.
 равен:
равен:
. 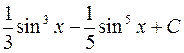 ;
;
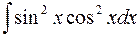 равен:
равен:
 ;
;
 равен:
равен:
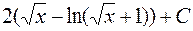 ;
;
В интеграле соответствуют
определению:
1-я пара: а; нижний предел интегрирования;
2-я пара: b; верхний предел интегрирования;
3-я пара: f (x); подынтегральная функция.
4-я пара: а; верхний предел интегрирования;
5-я пара: b; нижний предел интегрирования;
Интеграл  равен:
равен:
0;
Функция f (x) является нечётной. Тогда
интеграл  равен:
равен:
0;
Функция f (x) является чётной.
Тогда интеграл  равен:
равен:
.  ;
;
Формула среднего значения для
определённого интеграла 
и точки c Î [ a; b ]:
.  ;
;
 равен:
равен:
3;
 равен:
равен:
1;
Формула Ньютона-Лейбница: если
F(x) – первообразная функции f (x), то
 равен:
равен:
F(b) – F(a).
 равен:
равен:
.  ;
;
 равен:
равен:
1
 равен:
равен:
Эталон ответа: 40.
 равен:
равен:
Эталон ответа: 1.
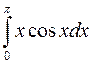 равен:
равен:
Эталон ответа: - 2.
 равен:
равен:
Эталон ответа: 1.
 равен:
равен:
Эталон ответа: 1.
 равен:
равен:
Эталон ответа: 0.
Площадь, ограниченная линиями
y = 12 x – 3 x 2 и y = 0 равна:
Эталон ответа: 32.
Площадь, ограниченная линиями
 и y = 17 – x 2, расположенными
и y = 17 – x 2, расположенными
в первом квадранте, равна:
Эталон ответа: 18.






