1. Постановка задачі наближеного диференціювання
2. Наближене диференціювання за допомогою інтерполяційного многочлена Ньютона
3. Графічне диференціювання
Чисельним диференціювання користуються для відшукання похідної функції, а також для наближеного обчислення похідної аналітично заданої функції, безпосереднє диференціювати яку тяжко.
Для відшукання похідної функції y=f(x) здійснюють інтерполюваня функції на розглядуваному відрізку [a;b] многочленом Pn(x) і його похідну приймають за похідну функції, тобто покладають
f’(x)=Pn’(x), a 
x b (1).
Аналогічно можна поступати і при знаходженні похідних вищих порядків, хоча для похідних порядку вище другого таку процедуру зазвичай не застосовують. Це зв’язано з тим, що похибка наближеної формули (1) мало зв’язана з похибкою інтерполювання. Дійсно, геометрично очевидно, що якщо ординати f(x1) i Pn(x) кривих y=f(x) i y=Pn(x) в точці х1 мало відрізняються одна від другої, то це не веде за собою незначної відмінності їх похідних f’(x1) i Pn’(x1) – кутових коефіцієнтів дотичних до цих кривих (рис). З зростанням порядку похідної точність чисельного диференціювання різко падає.
Для знаходження похідної f’(x) функції f(x), заданої таблицею з рівностоящими вузлами, використаємо многочлен Ньютона, представлений першою формулою, якщо х ближче до х0, чи другою, якщо х ближче до хn. Тоді із Pn(x)=Pn(x0+th)=y0+ 
,
враховуючи t= 
, одержимо
Pn’(x)=(Pn(x0+th))x’=(Pn)’t*tx’=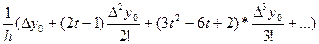 
,
Pn”(x)=(Pn’(xn+th))x’=(Pn’)t*tx’= 
.
Аналогічно із Pn(x)=Pn(xn+th)=yn+ 
,
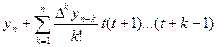враховуючи t= 
, одержимо
Pn’(x)=(Pn(xn+th))x’=(Pn)’t*tx’= 
,
Pn”(x)=(Pn’(xn+th))x’=(Pn’)t*tx’= 
.
Відмітимо, що за х0 чи хn можна прийняти будь–який проміжний вузол таблиці, тому зазвичай вибирають ближчий до х табличне значення аргументу.
Формули чисельного диференціювання значно спрощуються, якщо похідна відшуковується у вузлі інтерполяції, наприклад в точці хk. Прийнявши тоді хk за х0, одержимо t=0, а із формул одержуємо
Pn’(x0)= 
,
Pn”(x)= 
.
Чисельним диференціювання користуються для відшукання похідної функції, а також для наближеного обчислення похідної аналітично заданої функції, безпосереднє диференціювати яку тяжко.
Для відшукання похідної функції y=f(x) здійснюють інтерполюваня функції на розглядуваному відрізку [a;b] многочленом Pn(x) і його похідну приймають за похідну функції, тобто покладають
f’(x)=Pn’(x), a x b (1).
Аналогічно можна поступати і при знаходженні похідних вищих порядків, хоча для похідних порядку вище другого таку процедуру зазвичай не застосовують. Це зв’язано з тим, що похибка наближеної формули (1) мало зв’язана з похибкою інтерполювання. Дійсно, геометрично очевидно, що якщо ординати f(x1) i Pn(x) кривих y=f(x) i y=Pn(x) в точці х1 мало відрізняються одна від другої, то це не веде за собою незначної відмінності їх похідних f’(x1) i Pn’(x1) – кутових коефіцієнтів дотичних до цих кривих (рис). З зростанням порядку похідної точність чисельного диференціювання різко падає.
Для знаходження похідної f’(x) функції f(x), заданої таблицею з рівностоящими вузлами, використаємо многочлен Ньютона, представлений першою формулою, якщо х ближче до х0, чи другою, якщо х ближче до хn. Тоді із Pn(x)=Pn(x0+th)=y0+ ,
враховуючи t= , одержимо
Pn’(x)=(Pn(x0+th))x’=(Pn)’t*tx’= ,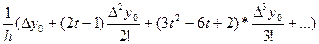
Pn”(x)=(Pn’(xn+th))x’=(Pn’)t*tx’= .
Аналогічно із Pn(x)=Pn(xn+th)=yn+ ,
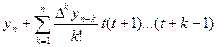враховуючи t= , одержимо
Pn’(x)=(Pn(xn+th))x’=(Pn)’t*tx’= ,
Pn”(x)=(Pn’(xn+th))x’=(Pn’)t*tx’= .
Відмітимо, що за х0 чи хn можна прийняти будь–який проміжний вузол таблиці, тому зазвичай вибирають ближчий до х табличне значення аргументу.
Формули чисельного диференціювання значно спрощуються, якщо похідна відшуковується у вузлі інтерполяції, наприклад в точці хk. Прийнявши тоді хk за х0, одержимо t=0, а із формул одержуємо
Pn’(x0)= ,
Pn”(x)= .
Суть графічного диференціювання полягає в тому, щоб по графіку функції, заданому на деякому відрізку [a;b], будується приблизно графік її похідної. Ця побудова основана на геометричному змісті похідної і по формулі Лагранжа скінчених приростів.
Нехай на малому відрізку [x0;x0+ 
x] заданий графік функції y=f(x). Із формули скінчених приростів слідує, що
f’( 
)= 
,
де х0< <x0+ x. Геометрично вираз, що стоїть справа, це тангенс кута нахилу хорди АВ, а розміщений зліва кутовий коефіцієнт дотичної до цієї точки Є(x0;x0+ x). Якщо x мале, то в якості можна взяти точку, що лежить посередині [x0;x0+ x], тобто =х0+ 
, тоді одержуємо наближену рівність f’(х0+ ) 
.
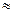
Для відшукання похідної в точці х0+ треба знайти тангенс кута нахилу хорди АВ. Для цього проведемо слідуючи побудови. Від точки О (або від любої другої точки зовні відрізка [x0;x0+ x]) вліво відкладемо одиничний відрізок ОК і проведемо KD||AB. Величина відрізка OD=OK*tg 
, де =<DKO=<BAC. Відповідно, OD=f’(х0+ ). Проведемо DN паралельно осі ох. Тоді точка N, що відповідає абсцисі х0+ , буде мати ординатою f’(х0+ ), тобто це точка графіка похідної функції f(x).
Нехай тепер функція f(x) задана на відрізку [a;b]. Відрізок [a;b] розіб’ємо на n частинних відрізки, не обов’язково рівних між собою, але так, щоб на кожному із них функція вела себе монотонно. На кожному частинному відрізку проведемо побудови, аналогічні описаним вище для відрізка [x0;x0+ x]. В кінці побудовані точки, аналогічні точці N, з’єднуємо ламаною, яка приблизно представляє графік похідної заданої функції f(x).
