1. Постановка задачі інтерполювання
2. Суть лінійного інтерполювання
3. Інтерполяційний многочлен Лангранжа
Загальна постановка задачі інтерполювання (інтерполяція – знаходження по ряду значень функції проміжних її значень) полягає у наступному: нехай на відрізку [a;b] в n+1 даних точках x 
,x 
,…,x 
відомі значення деякої функції f(x):
y =f(x ), y =f(x ), …, y =f(x ).
Треба визначити значення функції f(x) в точці хЄ[a;b], що не збігається з даною.
Звичайно, з такою постановкою задачі розв’язок задачі невизначено. Більш конкретно задача інтерполювання функції f(x) полягає в тому, щоб побудувати функцію F(x), що належить певному класу функцій і та що в даних точках х 
набуває тих же значень y =f(x ), що і функція f(x): F(x )=y (i=0,1,…,n).
Тоді для х Є[a;b] наближено покладають f(x)=F(x).
Точки x ,x ,…,x називають вузлами (чи полюсами) інтерполяції, а функцію F(x) – інтерполяційною функцією.
Звичайно інтерполяційну функцію шукають серед многочленів P (x), степінь яких не перевищує n і які задовольняють умові P (x )=y =f(x ), P (x )=y =f(x ),...,P (x )=y =f(x ). (1)
Неважко показати, що існує тільки один многочлен P (x) степені не вище n, що задовольняє всі умови (1).
Задача алгебраїчного (параболічного) інтерполювання функції y=f(x) на [a;b] полягає у відшуканні аналітичного вираження многочлена P (x), що задовольняє умові (1).
Многочлен P (x), визначений по умові (1), називається інтерполяційним многочленом для f(x), а формули для її побудови – інтерполяційними формулами.
Заміна функції y=f(x) її інтерполяційним многочленом f(x)=P (x), хЄ[a;b] називається інтерполюванням (алгебраїчним) функції.
Звичайно, при цьому виникає питання про оцінку похибки наближеної формули (2).
Геометричний зміст інтерполювання – заміна кривої y=f(x) параболою y=P (x) (порядка n), що проходить через задані точки (x ;y ), (х1;у1),...,(хn;yn).
Формулу (2) вважають інтерполяційною, якщо хЄ[x ;x ], тобто знаходиться між вузлами інтерполяції, якщо ж х 
[x ;x ], тобто знаходиться зовні відрізка, то формулу (2) називають екстраполяцією. В дальнішому ця відміність не враховується.
Лінійне інтерполювання полягає в заміні даної функції y=f(x) між любими двома вузлами інтерполяції х0, х1 лінійної функції визначеної з рівності
= 
.
Геометрично це означає заміну дуги кривої y=f(x) між точками М0(х0;у0) і М1(х1;у1) хордою М0М1 (рис.)
Якщо позначити х1-х0=h – крок інтерполяції, а у1-у0= 
у0, то формулу (3) можна записати у вигляді у=у0+ 
(х-х0) (4)
Лінійним інтерполюванням зазвичай користуються для визначення значення таблично заданої функції в точках, що не входять в таблицю. Крок h – це різниця між двома сусідніми табличними значеннями аргумента, в якості у0 брати ті значення, які відповідають меншому значенню аргумента.
ПРИКЛАД: Чотирьохзначні таблиці тригонометричних функцій складені для значення аргумента з кроком h=10. Обчислити з допомогою цих таблтць sin 35050’.
РОЗВ`ЯЗАННЯ: Значення аргумента х=35050’=35,8330 заключено в таблиці між 350 і 360. Для розглядуваного участка таблиці h=360-350=10, х-х0=0,8330, у0=0,588-0,574=0,014. Підставивши всі ці дані в (4), одержимо
sin 35050’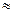 
0,574+0,833*0,014=0,586.
Із теорії чисельних методів відомо, що похибка лінійної інтерполяції R1(x)=f(x)-(у0+ (х-х0)) для два рази диференційованої функції f(x) оцінюється по формулі 
, (5) де M2=max 
, x0<x<x1. Лінійна інтерполяція дає стільки же правильних цифр, скільки їх в табличних значеннях функції, коли похибка інтерполяції не перевищує половини одиниці молодшого розряду табличних значень функції. Якщо таблиця складена, наприклад, з трьома правильними знаками, то для виконання лінійної інтерполяції повинна мати місце умова 
<0,5*10-3. В розглянутому прикладі f(x)=sin(x), тоді = 
і М2=1, h2=0,0172=0,0003 і по формулі (5) 
<0,00004=0,4*10-4<0,5*10-3. Умова виконана, відповідно, результат округлений до правильних цифр.
