совокупность всех первообразных F(x) + C;
 ¾ дифференциал неопределённого интеграла равен: f(x)dx; где F (x) – первообразная функции f (x).
¾ дифференциал неопределённого интеграла равен: f(x)dx; где F (x) – первообразная функции f (x).
F (x) – первообразная для функции f (x). Тогда  равен: f(x) + C; где С – произвольная постоянная.
равен: f(x) + C; где С – произвольная постоянная.
 равен: С;
равен: С;
 равен: х + С;
равен: х + С;
Соответствие неопределённых интегралов функциям:
1-я пара:  ; 2-я пара:
; 2-я пара:  ;
;
3-я пара:  ; 4-я пара:
; 4-я пара:  ;
;
5-я пара: 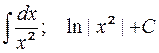 ; 6-я пара:
; 6-я пара:  .
.
Соответствие функций неопределённым интегралам:
1-я пара:  ; 2-я пара:
; 2-я пара:  ;
;
3-я пара:  4-я пара:
4-я пара:  ;
;
5-я пара 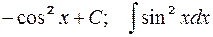 ; 6-я пара
; 6-я пара  .
.
Соответствие функций неопределённым интегралам:
1-я пара: 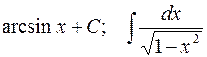 : 2-я пара:
: 2-я пара:  :
:
3-я пара:  ; 4-я пара:
; 4-я пара:  :
:
5-я пара:  ; 6-я пара:
; 6-я пара:  .
.
 равен:
равен:  ;
;
 равен:
равен:  ;
;
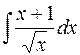 равен:
равен:  ;
;
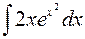 сводится к табличному заменой: t = x2;
сводится к табличному заменой: t = x2;
 равен:
равен:  ;
;
 сводится к табличному заменой: t = lnx;
сводится к табличному заменой: t = lnx;
 равен:
равен:  ;
;
 равен:.
равен:.  .
.
Соответствие функций неопределённым интегралам:
1-я пара:  ; 2-я пара:
; 2-я пара:  ;
;
3-я пара: 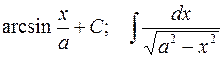 ; 4-я пара:
; 4-я пара:  ;
;
5-я пара:  ; 6-я пара
; 6-я пара  .
.
Формула интегрирования по частям. ò udv равен uv - òvdu;
Применить формулу интегрирования по частям в интеграле ò x 2ln xdx при u = lnx.
Применить формулу интегрирования по частям в интеграле ò x 2cos 2 xdx при u = x2;
ò xe - xdx равен:  ;
;
òarctg xdx равен:  ;
;
 равен: ln| x ± a | + C;
равен: ln| x ± a | + C;
 равен:
равен:  ;
;
 равен: arctg(x + 1) + C;
равен: arctg(x + 1) + C;
 равен:
равен:  ;
;
 равен:
равен:  ;
;
 равен:
равен:  ;
;
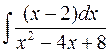 равен:
равен:  ;
;
 равен: 1
равен: 1
ln| x2 - 4x + 5 | + 9arctg (x - 2) + C;
 равен:
равен:  ;
;
Рациональная дробь (рациональная функции)  (Pn (x), Qm (x) – многочлены степени n и m) является правильной, если: n < m;
(Pn (x), Qm (x) – многочлены степени n и m) является правильной, если: n < m;
 равен:
равен:  .
.
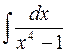 равен:
равен:  ;
;
 равен:
равен:  ;
;
 равен:
равен:  .
.
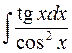 равен:
равен:  .
.
 равен:
равен:  ;
;
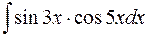 равен:
равен:  .
.
 равен:
равен:  ;
;
 равен:
равен:  ;
;
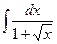 равен:
равен:  ;
;
В интеграле  соответствуют определению:
соответствуют определению:
1-я пара: а; нижний предел интегрирования;
2-я пара: b; верхний предел интегрирования;
3-я пара: f (x); подынтегральная функция.
4-я пара: а; верхний предел интегрирования;
5-я пара: b; нижний предел интегрирования;
Интеграл  равен: 0;
равен: 0;
Функция f (x) является нечётной. Тогда интеграл  равен: 0;
равен: 0;
Функция f (x) является чётной. Тогда интеграл  равен:.
равен:.  ;
;
Формула среднего значения для определённого интеграла  и точки c Î [ a; b ]:
и точки c Î [ a; b ]:
.  ;
;
 равен: 3;
равен: 3;
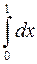 равен: 1;
равен: 1;
Формула Ньютона-Лейбница: если F (x) – первообраз. функции f (x), то  равен: F(b) – F(a).
равен: F(b) – F(a).
 равен:
равен:  ;
;
 равен: 1
равен: 1
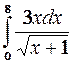 равен: Эталон ответа: 40.
равен: Эталон ответа: 40.
 равен: Эталон ответа: 1.
равен: Эталон ответа: 1.
 равен: Эталон ответа: - 2.
равен: Эталон ответа: - 2.
 равен: Эталон ответа: 1.
равен: Эталон ответа: 1.
 равен: Эталон ответа: 1.
равен: Эталон ответа: 1.
 равен: Эталон ответа: 0.
равен: Эталон ответа: 0.
Площадь, ограниченная линиями y = 12 x – 3 x 2 и y = 0 равна: Эталон ответа: 32.
Площадь, ограниченная линиями  и y = 17 – x 2, расположенными в первом квадранте, равна: Эталон ответа: 18.
и y = 17 – x 2, расположенными в первом квадранте, равна: Эталон ответа: 18.
Площадь, ограниченная линиями  и
и  , равна: Эталон ответа: 4.
, равна: Эталон ответа: 4.
Длина дуги кривой r = 2sin j (0 £ j < p), заданной в полярных координатах, равна: 2p.
Объём тела вращения вокруг Ох криволинейной трапеции, ограниченной линиями у 2 = х и у = х 2, равен V. Тогда  : Эталон ответа: 3.
: Эталон ответа: 3.
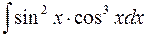 =
=  ;
;
В оценке определённого интеграла  для функции f (x) на отрезке [ a; b ] выполняется: m £ f (x) £ M;
для функции f (x) на отрезке [ a; b ] выполняется: m £ f (x) £ M;
Функция f (x) – непрерывна на [ a; +¥). Тогда 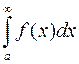 является: несобственным интегралом I-го рода;
является: несобственным интегралом I-го рода;
Несобственный интеграл 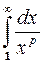 сходится, если: p > 1;
сходится, если: p > 1;
Несобственный интеграл  равен:
равен:  ;
;
Несобственный интеграл  равен:
равен:  ;
;
Несобственный интеграл  сходится, если: p < 1.
сходится, если: p < 1.
 существует, если функция f (x, y) в замкнутой области D: непрерывна;
существует, если функция f (x, y) в замкнутой области D: непрерывна;
Функция f (x, y) ³ 0 (f (x, y) ¹ 1 тождественно). Тогда  равен: объёму цилиндрического тела;
равен: объёму цилиндрического тела;
При разбиении области D на две подобласти D 1 и D 2 без общих внутренних точек интеграл  равен:
равен:
 ;
;
Область D ограничена линиями: y = j 1(x), y = j 2(x), x = a, x = b и j 1(x) £ j 2(x), a < b. Тогда интеграл  равен:
равен:  ;
;
Область D ограничена линиями: x = j 1(y), x = j 2(y), y = c, y = d и j 1(y) £ j 2(y), a < b. Тогда интеграл  равен:
равен:
1.  ; 2.
; 2.  ;
;
+3.  ; 4.
; 4.  .
.
Изменив порядок интегрирования в интеграле  , получим:
, получим:
1. 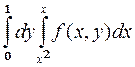 ; 2.
; 2.  ;
;
3.  ; +4.
; +4.  .
.
Площадь S плоской фигуры D с помощью двойного интеграла вычисляется по формуле:
+1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  .
.
В цилиндрических координатах  имеет вид:
имеет вид:
1. 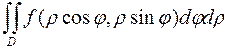 ; 2.
; 2.  ;
;
+3.  ; 4.
; 4.  .
.
Площадь области, ограниченной кривыми линиями y = 2 – x 2 и y = x, равна S. Тогда 6 S равны:
Эталон ответа: 27.
Объём V тела, ограниченного поверхностями z = 6 – 3 x – 2 y, z = 0, x = 0, y = 0 равен:
Эталон ответа: 6.
Пусть V – область интегрирования: 0 £ x £ 1, 0 £ y £ 3, 0 £ z £ 4. Тогда  равен:
равен:
Эталон ответа: 12.






