Фігура, центр ваги якої треба знайти, показана на рисунку:
Шукаємо масу фігури:
В силу симетрії фігури, 
.
А
Знайти момент інерції відносно осі однорідного тіла (густина), обмеженого параболоїдом і площиною.
На площину ХОZ тіло проектується у коло: 
, перейдемо до полярних координат:
Б
Знайти момент інерції однорідного тіла (густина), обмеженого поверхнями відносно осі.
На площину УОХ тіло проектується у коло 
, перейдемо до полярних координат:
А
Знайти момент інерції однорідного тіла (густина), обмеженого поверхнями відносно осі.
На площину УОZ тіло проектується у коло 
, перейдемо до полярних координат:
В
Знайти довжину дуги кривої, заданої рівнянням.
А
Знайти довжину дуги кривої, заданої рівняннями.
Б
Знайти довжину дуги кривої, заданої рівнянням.
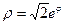
А
Знайти довжину дуги кривої.
Б
Знайти роботу сили при переміщенні вздовж лінії від точки до точки:, – відрізок прямої,.
Роботу поля шукаємо за формулою: 
Рівняння прямої: y = 0,5x + 2
Б
Знайти площу частини площини, вирізаної координатними площинами.
Площина показана на рисунку
В
194 Обчислити потік векторного поля 
через зовнішню сторону замкненої поверхні 
. 
; 
.
Потік шукаємо за формулою: 
Замкнена поверхня показана на рисунку:
Г
Знайти потік векторного поля через повну поверхню конуса застосувавши формулу Остроградського.
Потік шукаємо за формулою:
Перейдемо до полярних координат: 
А
196 Знайти площу частини площини 
, вирізаної координатними площинами.
Площина показана на рисунку
В
Задано векторне поле і площина (), яка разом з координатними площинами утворює піраміду V. Нехай – основа піраміди, яка належить площині (); – контур, який обмежує, – зовнішня нормаль до. Обчислити циркуляцію векторного поля вздовж замкненого контура, застосувавши формулу Стокса до контура і обмеженої ним поверхні з нормаллю.
Циркуляцію знайдемо за формулою: 
Визначаємо:
Піраміда показана на рисунку.
Г
Задано векторне поле і площина (), яка разом з координатними площинами утворює піраміду V. Нехай – основа піраміди, яка належить площині (); L – контур, який обмежує, – зовнішня нормаль до. Обчислити циркуляцію векторного поля вздовж замкненого контура, застосувавши формулу Стокса до контура і обмеженої ним поверхні з нормаллю.
Циркуляцію знайдемо за формулою:
Визначаємо:
Піраміда показана на рисунку
В
Обчислити дивергенцію поля в точці.
А
Обчислити ротор векторного поля.
Ротор шукаємо за формулою Стокса:
Б