Перейдемо до параметричного задання функції:



 =
=  А
А
Обчислити, де – дуга параболи.
Представимо у виді: 



 =
=  А.
А.
Обчислити, де – частина параболи.
Представимо у виді: 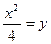



 =
= 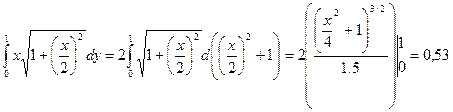 Б
Б
Обчислити, де – частина параболи.



 =
=  В
В
Обчислити, де – частина параболи.



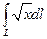 =
=  В
В
Обчислити, де – частина параболи.
Представимо у виді: 


 =
=  А
А
Обчислити, де – частина параболи.



 =
=  Г
Г
Обчислити, де – частина параболи.
Нехай  , тоді
, тоді 

 =
= 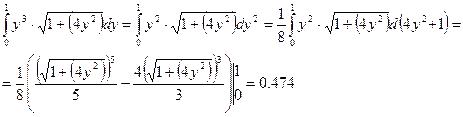 Г
Г
Обчислити, де – верхня половина еліпса, яку проходять за годинниковою стрілкою.



 В
В
Обчислити, де – нижня половина еліпса, яку проходять за годинниковою стрілкою.

 Б
Б
Обчислити, де – контур трикутника, що обмежений осями координат і прямою, який проходять проти годинникової стрілки.
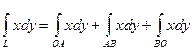
Для відрізка ОА: 
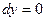

Для відрізка АВ: 
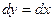

Для відрізка ВО: 

 Б
Б
Обчислити де – контур трикутника, що обмежений осями координат і прямою, який проходять проти годинникової стрілки.

Для відрізка ОА: 
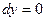

Для відрізка АВ: 
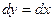

Для відрізка ВО: 

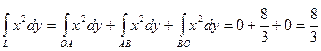 А
А
Обчислити, де – контур трикутника, що обмежений осями координат і прямою, який проходять проти годинникової стрілки.

Для відрізка ОА: 
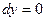

Для відрізка АВ: 
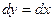

Для відрізка ВО: 

 В
В
Обчислити, де – контур трикутника, що обмежений осями координат і прямою, який проходять проти годинникової стрілки.

Для відрізка ОА: 
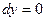

Для відрізка АВ: 
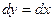

Для відрізка ВО: 

 Б
Б
Обчислити, де – контур трикутника, що обмежений осями координат і прямою, який проходять проти годинникової стрілки.

Для відрізка ОА: 
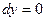

Для відрізка АВ: 
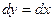

Для відрізка ВО: 

 Б
Б
Обчислити, де – дуга параболи, що знаходиться у верхній півплощині і яку проходять за годинниковою стрілкою.
 розглядаємо ділянку параболи між точками (0;0) та (2;0)
розглядаємо ділянку параболи між точками (0;0) та (2;0)
 =
=  А
А
Обчислити, де – ламана АВC, що з’єднує точки А(-2;0), В(0;4), C(2;0).
Для відрізка АВ: 

 =
= 
Для відрізка ВС: 
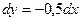
 =
= 
Для відрізка СА: 
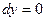
 =0
=0
 Б
Б
Обчислити, де – відрізок прямої від точки А(-2;0) до точки B(2;0).

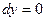
 =0 Г
=0 Г
Обчислити, де – дуга параболи від точки А(0;0) до точки B(1;1).
 =
=  А
А
Обчислити, де – дуга параболи від точки А(0;0) до точки B(1;1).
 =
=  А
А
Обчислити, де – відрізок прямої від точки А(0;0) до точки B(1;1).
Рівняння прямої АВ: 
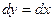
 =
=  А
А
Обчислити, де – відрізок прямої від точки А(0;0) до точки B(1;2).


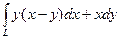 =
=  В
В
Обчислити, де – дуга параболи від точки А(0;0) до точки B(1;2).

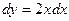
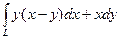 =
=  Б.
Б.
Обчислити, де – дуга параболи від точки А(0;0) до точки B(1;2).
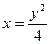

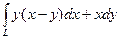 =
=  Д
Д
Обчислити, де – ламана АВC: А(0;0), В(2;0), C(4;5).

Для відрізка АВ: 
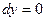

Для відрізка ВС: 


 Б
Б
Обчислити, де – дуга параболи від точки А(-1;1) до точки B(1;1).

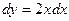
 =
= 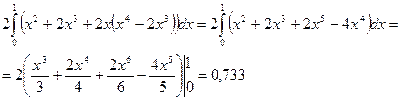 Г
Г
Обчислити, де – дуга параболи від точки А(-1;2) до точки B(1;2).


 =
=  В
В
Обчислити, де – дуга кривої від точки А(0;1) до точки B(-1;e).
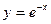

 =
=  А
А
Обчислити, де – дуга параболи від точки А(0;0) до точки B(1;2).

 =
=  Б
Б
Обчислити, де – дуга кривої від точки А(1;0) до точки B(e;1).


 =
=  В
В
Обчислити, де – дуга синусоїди від точки А(;0) до точки В(0;0).


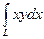 =
=  Б.
Б.
Обчислити, де – відрізок прямої від точки А(2;1) до точки В(1;2).
Рівняння прямої АВ: 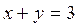

 =
=  В
В
Обчислити, де – крива:.

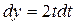

 =
=  А.
А.
101 Обчислити  , де σ – поверхня частини площини x+ 2 y+ 3 z= 6, що розміщена в першому октанті.
, де σ – поверхня частини площини x+ 2 y+ 3 z= 6, що розміщена в першому октанті.
З рівняння площини маємо: 



 А.
А.
102 Обчислити  , де σ – поверхня частини площини x+2y+3z=6, що розміщена в першому октанті.
, де σ – поверхня частини площини x+2y+3z=6, що розміщена в першому октанті.
З рівняння площини маємо: 


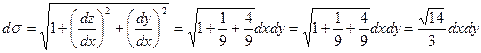
 Б.
Б.




