Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных 
функций.
Различают два класса нелинейных регрессий:
I. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например параболы 2-го,3-го порядка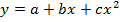 
; y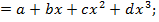 
гипербола 
;
II. Регрессии, нелинейные по оцениваемым параметрам: степенная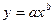 
Показательная 
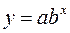экспоненциальная 
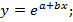Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов.
Например для 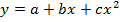получим систему следующих нормальных уравнений, для гиперболы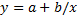 
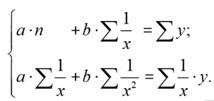
Данная функция может использоваться для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота.
II.1.Нелинейные модели внутренне линейные (может быть приведена к линейному виду). II.2. Нелинейные модели внутренне нелинейные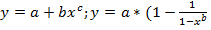 
)
Корреляция и детерминация для нелинейной регрессии.
|
|
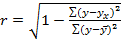или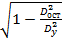 
Величина данного показателя находится в [0;1].Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Квадрат индекса корреляции - индекс детерминации, который характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака: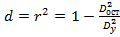 
= 
; 
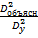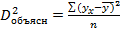
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по F -критерию Фишера: 
n – число наблюдений, m – число параметров при переменной x. Фактическое значение F -критерия сравнивается с табличным при уровне значимости α и числе степеней свободы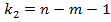 
(для остаточной суммы квадратов) и 
(для факторной суммы квадратов).
Коэффициенты эластичности для разных видов регрессионных моделей.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. В степенной функции параметр b является коэффициентом эластичности, в других функциях коэффициент эластичности зависит от значения фактора x.
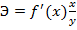,где 
- первая производная, характеризующая соотношение прироста результата и фактора для соответствующей формы связи.
