Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида 
Уравнение позволяет по заданным значениям фактора x находить теоретические значения результативного признака, подставляя в него фактические значения фактора x. Оценки параметров линейной регрессии могут быть найдены разными методами:
1)Графически взаимосвязь двух показателей изображается с помощью поля корреляции. В системе координат на оси абсцисс откладывают значение факторного пр-ка, а на оси ординат - результат признака. Каждое пересечение линий обозначает точку, при отсутствии тесных связей имеет место беспорядоченное изображение точек на графике. Чем сильнее связь между показателями, тем теснее будут группироваться точки вокруг воображаемой линии.
2) Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Используется следующая система линейных уравнений для оценки параметров a и b: 
Решая систему уравнений, найдем искомые оценки параметров a и b. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы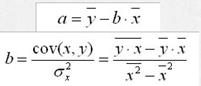 
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Формально a – значение y при х = 0. Если признак-фактор x не может иметь нулевого значения, то вышеуказанная трактовка свободного члена a не имеет смысла, т.е. параметр a может не иметь экономического содержания. Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции. Выделяют следующие количествен. критерии оценки тесноты связи в зависимости от величины коэффициента корреляции:
• до ±0,3 практически отсутствует
• ±0,3─0,5слабая
• ±0,5─0,7 умеренная
• ±0,7─0,9 сильная
• ±0,9─0,99 очень сильная
• r = 0 связь отсутствует
• r = 1 связь прямая функциональная зависимая
• r = -1 обратная.Знак коэффициента корреляции показывает направление связи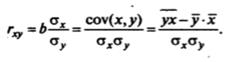 
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, при этом выдвигается нулевая гипотеза, которая предполагает, что в какой-то момент времени при определенных условиях коэффициент регрессии равен нулю, т.е b = 0, тогда a = y. Расчету F -критерия предшествует анализ дисперсии. Дисперсия - средний квадрат отклонения индивидуальных значений признака от их средней величины. Корень из дисперсии есть среднее квадратическое отклонение, которая является обобщающей характеристикой размеров вариации признака совокупности. Для проведения анализа дисперсии общая сумма квадратов раскладывается на объясненную(факторную) и не объясненную(остаточную).
При заданном наборе переменных х и у расчетное значение, теоретически у является в линейной регрессии функцией только одного параметра b, поэтому в парной линейной регрессии факторное СКО имеет степень свободы 1. Остаточная имеет степень свободы (n-2), степень свободы общей СКО (n-1). Разделив каждое СКО на соответствующую им степень свободы получим СКО на одну степень свободы. Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии на одну степень свободы рассчитываем F -критерий Фишера: 
. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для опровержения нулевой гипотезы необходимо, чтобы факторная дисперсия превышала остаточную дисперсию в несколько раз. Разработаны таблицы критических значений F -критерия при разных уровнях существенности. Табличное значение F -критерия- это max величина отношения дисперсий, которая может иметь место при случайном их расхождении для заданного уровня вероятности нулевой гипотезы. Вычисленное значение F -критерия признается достоверным, если оно больше или равно табличному. В этом случае нулевая гипотеза отклоняется и делается вывод о существенности связи. Если величина меньше табличной, то уравнение регрессии признается статистически незначимой - нулевая гипотеза принимается. Величина F -критерия связанна с коэффициентом корреляции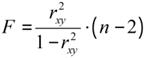 
Для оценки значимости отдельных параметров уравнения в парной линейной регрессии по каждому из параметров определяется его стандартная ошибка 
; 
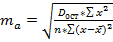
Величина стандартной ошибки совместно с t -распределением Стьюдента применяется для проверки существенности коэффициента регрессии и параметра а и расчета их доверительных интервалов. Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t -критерия Стьюдента: 
или 
которое затем сравнивается с табличным значением. Если расчетное значение t -критерия больше табличного, гипотезу о несущественности параметров можно отклонить. Далее строится доверительный интервал. 
(для b аналогично)Если 0 не входит в интервал, то параметры существенны.
