Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
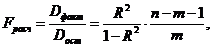
где Dфакт – факторная сумма квадратов на одну степень свободы;
Dост – остаточная сумма квадратов на одну степень свободы;
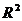- коэффициент (индекс) множественной детерминации;
m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов);
n – число наблюдений.
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы: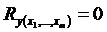 
(гипотеза о незначимости уравнения регрессии).
По таблицам распределения Фишера находят критическое значение F -критерия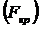 
. Для этого задаются уровнем значимости 
(обычно его берут равным 0,05) и двумя числами степеней свободы 
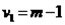и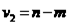 
. Здесь m – число параметров модели.
Сравнивают фактическое значение F -критерия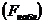 
с табличным 
.
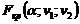Если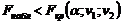 
, то гипотезу о незначимости уравнения регрессии не отвергают. Если 
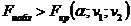, то выдвинутую гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии.
Частный F-критерий оценивает статистическую значимость присутствия каждого факторов в уравнении. Необходимость такой оценки вызвана тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативно признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель.
Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на однй степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния 
как дополнительно включенного в модель фактора. В общем виде для фактора частный F-критерий определится как:
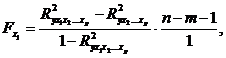
где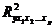 
- коэффициент множественной детерминации для модели с полным набором факторов;
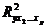- тот же показатель, но без включения в модель фактора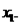 
n – число наблюдений;
m – число параметров в модели (без свободного члена) или число независимых переменных модели.
По таблицам распределения Фишера находят критическое значение F -критерия 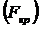. Для этого задаются уровнем значимости (обычно его берут равным 0,05) и двумя числами степеней свободы 
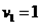и 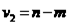. Здесь m – число параметров модели.
Сравнивают фактическое значение F -критерия 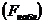с табличным 
.
Если Fкр меньше табличного, то включение в модель данного фактора x1 после введения в нее фактора x2 нецелесообразно, и наоборот.
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения:
где bi - коэффициент чистой регрессии при факторе xi;
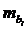- средняя квадратичная ошибка коэффициента регрессии bi.
Она может быть определена по следующей формуле:
где 
- среднее квадратическое отклонение для фактора y;
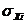- среднее квадратическое отклонения для фактора xi;
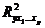- коэффициент детерминации для уравнения множественной регрессии;
- коэффициент детерминации для зависимости фактора xi со всеми другими факторами уравнения множественной регрессии;
n-m -1 – число степеней свободы для остаточной суммы квадратов отклонений.
Далее находят табличное значение t -критерия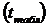 
. Для этого задаются уровнем значимости (обычно его берут равным 0,05) и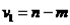 
. Здесь m – число параметров модели.
Сравнивают фактическое значение t -критерия с табличным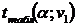 
.
Если фактическое tbi меньше табличного, то коэффициент регрессии bi статистически незначим, и формируется преимущественно под влиянием случайных факторов; и наоборот.
Аналогично оценивается статистическая значимость индекса множественной корреляции:
(k – число независимых переменных модели).
Адекватность регрессионной модели оценим опять же с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений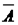 
– не более 8-10%.
