Оценка параметров уравнения парной регрессии.
Эконометрические модели делятся на линейные и нелинейные.
Построение линейной регрессии сводится к оценке ее параметров – а и b. Оценка параметров линейной регрессии могут быть найдены разными методами.Можно обратиться к полю корреляции и,выбрав на графике две точки,провести через них прямую линию,затем по графику найти значения параметров.Параметрaопределим как точку пересечения линии регрессии с осью oy,а параметр bоценим исходя из угла наклона линии регрессии как dy/dx,где dy – приращение результата y,а dx – приращение фактора x,т.е.
= a+ bx
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК)
Линейная модель парной регрессии: у=bх+a+E
b - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
a - это свободный член, расчетная величина, содержания нет.
E - это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
Присутствие e в модели свидетельствует о том, что функциональной зависимости м\у у и х нет. На изменение у оказывает влияние не только фактор х, но и какие-то др не учтенные моделью факторы.
Первой задачей регрессионного анализа явл получение значения параметров a и b. Найтэтои параметры мы не можем (пришлось бы обследовать ген совокупность), поэтому находим выборочные оценки этих параметров.
ŷ = a + b x
Для нахождения выборочных оценок используем метод НК
решением системы нормальных уравнений будет:
выборочные оценки для ур-я (1)
очевидно, что мин регрессия будет иметь место только в том случае, если 
, если хi совпадает с 
.
В этом случае зависимость отсутствует.
Нелинейная модель. уравнение зависимости между Уи Х может быть представлено степенной функцией У от Х, 
, показательной 
, гиперболической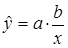 
и д.р.
Для оценки параметров в этих случаях метод наименьших квадратов можно применять после логарифмирования, либо после введения новой переменной.
Для показательной функции:
lny=lna+xlnb
Y α β
Y = α + х β Þ а = еα; b=еβ
Для степенной функции
ln y=lna+bln x
Y α X
Y = α + β X
Для гиперболической функции
у=а+b/x
1/х=Х
У=а+bХ
Абсолютные и относительные показатели силы связи в уравнениях парной регрессии.
К показателям тесноты связи относятся:
1) коэффициент линейной корреляции
2) коэффициент детерминации.
3)коэффициент эластичности;
1.Уравнение регрессии всегда дополняется показателем тесноты связи.При использовании линейной регрессии в качестве такого показателя выступает линейный коэф корреляции 
Имеются разные модификации формулы линейного коэфкорреляции,например:
= 
= 
или
Как известно,линейныйкоэф корреляции находится в границах -1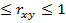 
Если коэф регрессии b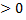 
,то 0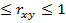
И наоборот,при b 
-1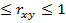
2)Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэф корреляции 
yx = 
Соответственно величина 1- 
характеризует долю дисперсии y,вызванную влиянием остальных не учтенных в модели факторов.Линейныйкоэф корреляции по содержанию отличается от коэф регрессии.
3)Линейный коэф корреляции как измеритель тесноты линейной связи признаков логически связан не только с коэф регрессии b,но и с коэфэластичности,который является показателем силы связи,выраженным в процентах.При линейной связи признаков x и yсредний коэф эластичности в целом по совокупности определяется как
Коэффициент частной эластичности рассчитывается по формуле:
= 
т.е. его формула по построению близка к формуле линейного коэф корреляции
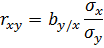
Несмотря на схожесть этих показателей,измерителем тесноты связи выступает линейный коэф корреляции (
),а коэф регрессии (
И коэф эластичности (
– показатели силы связи; коэф регрессии является абсолютной мерой,т.к. имеет единицы измерения,присущие изучаемым признакам y иx,а коэф эластичности – относительным показателем силы связи,потому что выражен в процентах.
Несмотря на всю важность измерителя тесноты свзяи,в эконометрике больший практический интерес приобретает коэф детерминации 
yx
,т.к. он дает относительную меру влияния фактора на рез-т,фиксируя одновременно и роль ошибок,т.е. случайных составляющих в формировании моделируемой переменной.Чем ближе коэф детерминации к 1,тем в большей степени уравнение регрессии пригодно для прогнозирования.
