Методи знаходження оцінок в умовах автокореляції

Для оцінювання параметрів економетричних моделей з автокорельованими залишками в основному використовуються наступні методи:

1) метод Ейткена (УМНК);

2) метод перетворення вихідної інформації;

3) метод Кочрена – Оркатта;

4) метод Дарбіна.

Метод Ейткена (УМНК) Система рівнянь для оцінки параметрів моделі на основі методу Ейткена запишеться так: або 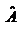‑ вектор оцінок параметрів економ-ої моделі; ‑ матриця не залеж змінних; ‑ матриця, транспон-а до матриці X; ‑ матриця, обернена до матриці кореляції залишків; ‑ матриця, обернена до матриці V, де , а - залишкова дисперсія; Y ‑ вектор залеж змінних. Звідси або Отже, щоб оцінити параметри моделі на основі методу Ейткена, треба сформ-и матрицю S або V. Матриця S має вигляд:

У цій симетричній матриці виражає коефіцієнт автокореляції s -го порядку для залишків 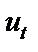. Очевидно, що коефіцієнт автокореляції нульового порядку дорівнює 1.

Оскільки коваріація залишків при s > 2 часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд:

(8.22)

Таку матрицю іноді пропонується використовувати при оцінюванні параметрів моделі з автокорельованими залишками за методом Ейткена.

Покажемо, як використовується циклічний коефіцієнт кореляції для обчислення r.

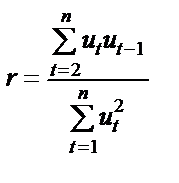або

де u_t — величина залишків у період t; u_t– ₁ — величина залишків у період t – 1; n — число спостережень.

Якщо , то .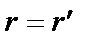

Зауважимо, що параметр r (або ) має зміщення. Тому, використовуючи такий параметр для формування матриці S, необхідно скоригувати його на величину зміщення

де — величина зміщення (m — кількість незалежних змінних), або

Матриця , де — залишкова дисперсія, що визначається за формулою

де — вектор, транспонований до вектора залишків u; n – m – 1 — число ступенів свободи.

Дисперсія залишків з урахуванням зміщення обчислюється так:

Величину l можна обчислити методом 1МНК з допомогою авторегресійного рівняння x_t = l x_t– ₁ + e _t. У такому разі

де x_t взято як відхилення від свого середнього значення.

При реалізації алгоритму Ейткена для оцінки параметрів моделі застосовують такі п’ять кроків.

Крок 1. Оцінка параметрів моделі за методом 1МНК.

Крок 2. Дослідження залишків на наявність автокореляції.

Крок 3. Формування матриці коваріації залишків V або S.

Крок 4. Обернення матриці V або S.

Крок 5. Оцінка параметрів методом Ейткена, тобто згідно з (8.18), (8.19).

Метод перетворення вихідної інформації. Випадок, коли залишки задовольняють авторегресійну модель першого порядку, допускає альтернативний підхід до пошуку оцінок параметрів моделі за допомогою двокрокової процедури:

1) перетворення вихідної інформації при застосуванні для цього параметра r;

2) застосування 1МНК для оцінки параметрів на основі перетворених даних.

Для цього треба знайти матрицю перетворення T, щоб модель

(8.23)

мала скалярну дисперсійну матрицю

Розглянемо матрицю T ₁ розміром n ´ n:

(8.24)

Безпосереднім множенням легко переконатись, що

А це означає, що можна застосувати 1МНК до перетворених даних і , які мають вигляд

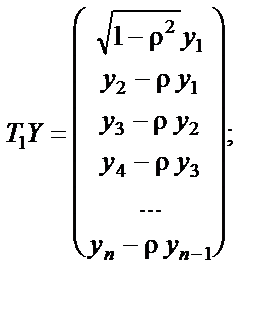
Іноді для перетворення вихідної інформації використовується матриця 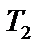розміром (n – 1) ´ n, яка отримується з матриці внаслідок викреслювання першого рядка:

Неважко показати, що застосування 1МНК до даних і дає таку саму оцінку параметрів моделі, як і метод Ейткена, а для даних і 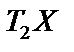— забезпечує порівняно добру апроксимацію.

Метод Кочрена – Оркатта. Розглянемо алгоритм:

Крок 1. Приймається гіпотеза і мінімізується на основі 1МНК сума квадратів: . Отже, так само й далі обчислюються параметри для моделі (8.25).

Крок 2. Знаходяться залишки і на основі критерію Дарбіна — Уотсона перевіряється нульова гіпотеза відносно автокореляції залишків. Якщо гіпотеза відхиляється, то переходять до кроку 3.

Крок 3. На даному кроці мінімізується сума квадратів відхилень:

де і — оцінки параметрів, знайдені на першому кроці 1МНК. У результаті параметр 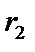визначається як коефіцієнт регресії залишків, знайдених 1МНК, на їх лагові змінні, які стосуються минулого періоду.

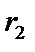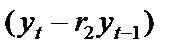Крок 4. Використовуючи значення оцінки параметра , визначають оцінки параметрів і на основі 1МНК, який застосовується до перетворених даних і .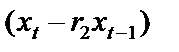

Крок 5. Визначаються залишки і перевіряються на наявність автокореляції. Якщо гіпотеза про наявність автокореляції відхиляється, то ітеративний процес припиняється. У противному разі переходимо до кроку 3, де використовуються знайдені оцінки параметрів і .

Коли ітеративний процес припиняється, то виконується перевірка значущості параметрів з допомогою останньої економетричної моделі. У такому разі звичайні формули дадуть обгрунтовані оцінки дисперсій залишків.

Метод Дарбіна. Алгоритм:

Крок 1. Підставимо значення залишків, яке підпорядковане авторегресійній моделі першого порядку до економетричної моделі . Тоді дістанемо , де .

Звідси

де 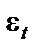має скалярну матрицю дисперсій.

Згідно з 1МНК визначаються параметри цієї моделі, куди входить і коефіцієнт . У результаті обчислень маємо .

Крок 2. Значення використовується для перетворення змінних і 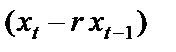, а 1МНК застосовується до перетворених даних. Коефіцієнт при 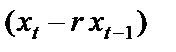є оцінкою параметра , а вільний член, поділений на , оцінює параметр .