Для вимірювання сили лінійних зв’язків різних пар змінних використовується коефіцієнт парної кореляції. Причому для будь-яких двох факторів x і та x j коефіцієнт кореляції лежить в межах:
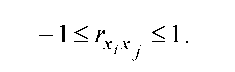
Якщо 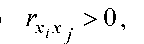 то випадкові величини x і x j зв’язані додатною кореляцією (при зростанні однієї друга теж зростає); якщо
то випадкові величини x і x j зв’язані додатною кореляцією (при зростанні однієї друга теж зростає); якщо 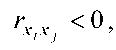 то випадкові величини x і x j зв’язані від’ємною кореляцією (при зростанні однієї друга спадає). Коефіцієнт парної кореляції між змінними можна визначити за формулою
то випадкові величини x і x j зв’язані від’ємною кореляцією (при зростанні однієї друга спадає). Коефіцієнт парної кореляції між змінними можна визначити за формулою 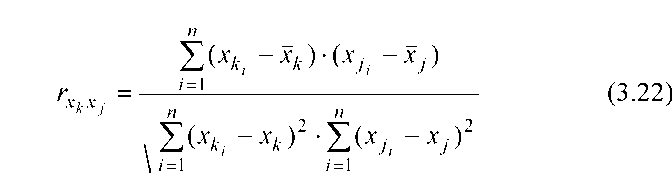
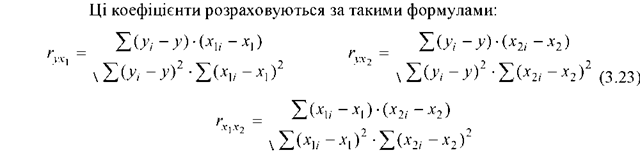
Крім коефіцієнтів парної кореляції вводяться коефіцієнти частинної кореляції. Частинною кореляцією між факторами x і Х j називається кореляційна залежність між цими факторами при фіксованих значеннях інших факторів [2].
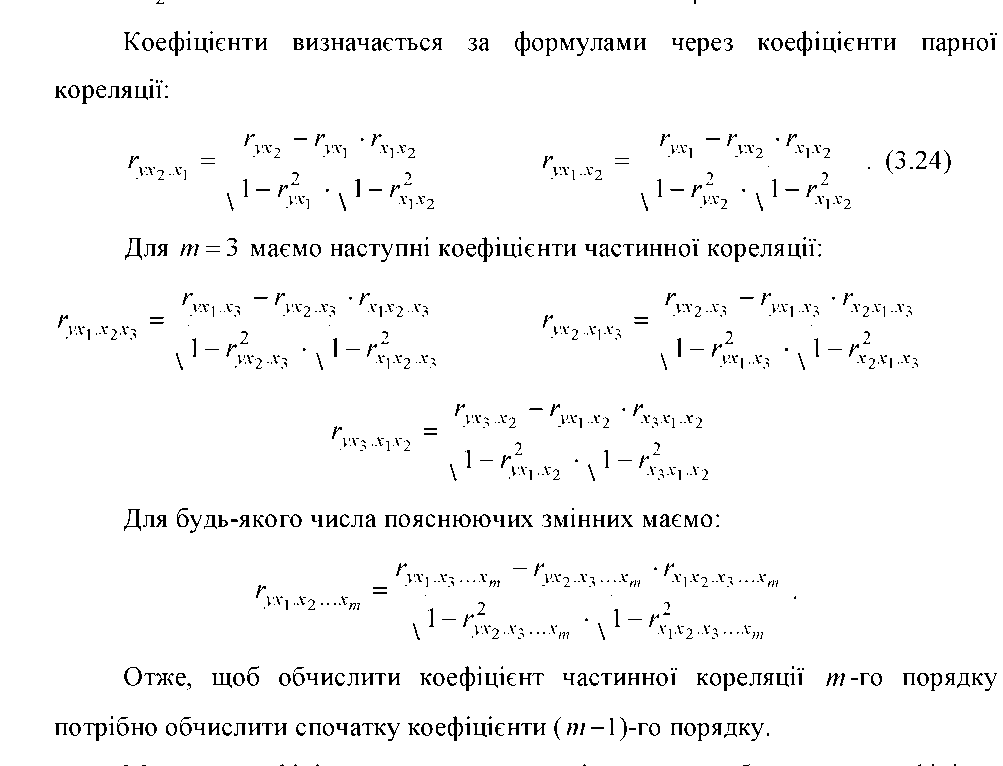
. В економетричній моделі з 2-ма змінними (однофакторній) ми дали поняття коефіцієнта кореляції r і коефіцієнта детермінації d. У випадку економетричної моделі з кількістю змінних більшою ніж 2, вводиться поняття коефіцієнта множинної кореляції R. Він визначається як коефіцієнт кореляції між y та yˆ по формулі:

21. Постановка задачі в матричній формі та основні припущення МНК для загального випадку. МНК в матричній формі.
Лінійну багатофакторну економетричну модель зручно розглядати за допомогою теорії матриць. Для цього запишемо модель (3.1) для кожного окремого спостереження:
1. Лінійну багатофакторну економетричну модель зручно розглядати за допомогою теорії матриць. Для цього запишемо модель (3.1) для кожного окремого спостереження:
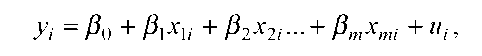 (3.11)
(3.11)
де  - і-е значення залежної змінної;
- і-е значення залежної змінної; 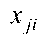 - і-е значення ] -ої незалежної
- і-е значення ] -ої незалежної
змінної; 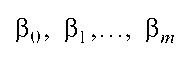 - невідомі детерміновані параметри; - і-е значення
- невідомі детерміновані параметри; - і-е значення
випадкової змінної. Можна (3.11) подати у вигляді системи:
 (3.12)
(3.12)
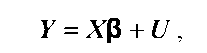
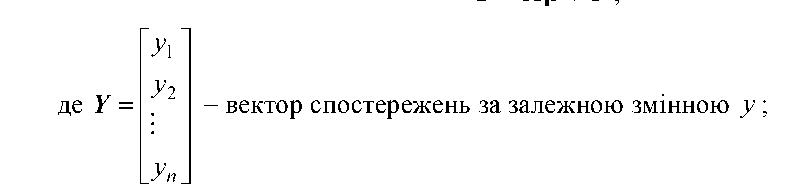

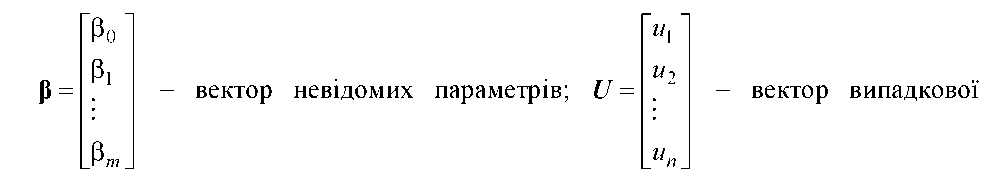
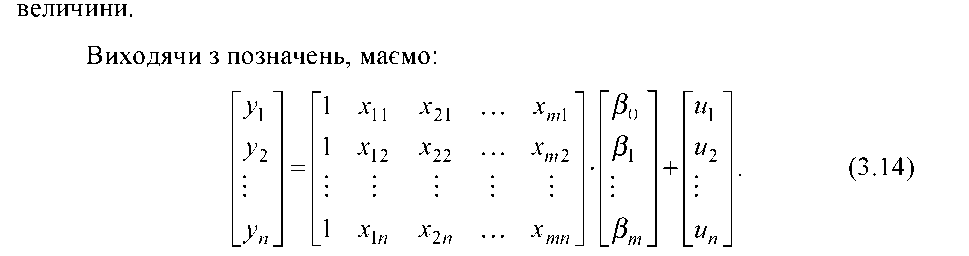 матриця спостережень за т змінними х1, х2.
матриця спостережень за т змінними х1, х2.
У матричному вигляді основні припущення лінійної багатофакторної економетричної моделі матимуть вигляд:
 Оскільки для випадкової величини властива гомоскедастичність та відсутній зв’язок між випадковими величинами, то:
Оскільки для випадкової величини властива гомоскедастичність та відсутній зв’язок між випадковими величинами, то:
| 'а 2 | ... 0 | '1 | 0. | . 0" | |||
| М (ии') = | а2 | ... 0 | = а 2 | 1. | . 0 | ||
| _ 0 | ... а2 _ | 0. | . 1_ |
| : а 2 Е, (3.15) |
де Е - одинична матриця розміру п х п.
2. Для того щоб знайти оцінки параметрів р запишемо економетричну модель у матричному вигляді, використавши попередні позначення і наступні:
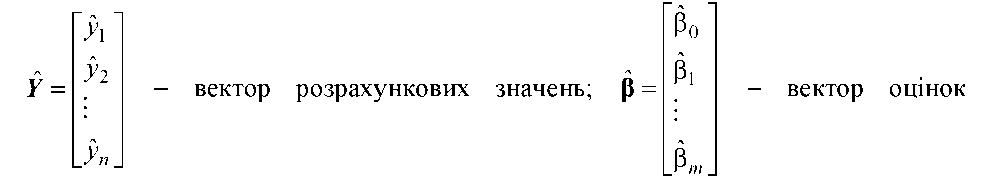
|
| параметрів; e = |
 Лінійна багатофакторна економетрична модель має вигляд:
Лінійна багатофакторна економетрична модель має вигляд:
Вектор оцінок параметрів знайдемо методом найменших квадратів, мінімізуючи суму квадратів залишків:

|
e(ß) = Е ef = е’е = (Y - *ß)'(Y - Xß) = Y Y - 2ß'X Y + ß'XXß ® min, (3.17)
i = 1
де символ штрих (') означає операцію транспонування.
 Зауваження. При перетворенні (3.17) враховані властивості транспонованих матриць: (Xß)' = ß 'X'; ß 'X Y = Y Xß.
Зауваження. При перетворенні (3.17) враховані властивості транспонованих матриць: (Xß)' = ß 'X'; ß 'X Y = Y Xß.
| Знайдемо частинну похідну виразу (3.17) за компонентами вектора ß і прирівняємо її до нуля: |
| öe(ß) |
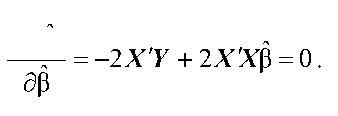
| Звідси отримуємо систему рівнянь в матричній формі: |
| X Xß = X Y |
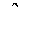
| /V /V /V /V /V /-Ч М (3 т - 3 т)(3 0 -3с) М (3 т -3 т)(31 - в) ■ М (3 т -3т)2 _ |
(3.18) є системою нормальних рівнянь МНК для знаходження оцінок (3 0,
3і3т в матричній формі. Якщо визначник матриці X'X не дорівнює нулю
(д^(ХX) Ф 0), то існує обернена матриця (XX)-1 і розв’язок системи (3.18)
буде вектор-стовпець
в = (X X)-1X У (3.19)
Рівняння (3.19) є фундаментальним результатом для визначення невідомих параметрів у матричному вигляді.
22. Дисперсійно-коваріаційна матриця  . Матриця кореляції.
В економетричній моделі У = XP + и вектор и і залежний від нього вектор У є випадкові змінні. Оскільки в ми визначаємо з виразу в = (XX)-1X'У в який входить У, то в також можна вважати випадковою
функцією оцінювання параметрів моделі. Тому для характеристики в
необхідно знати не тільки математичне сподівання, а й дисперсію, коваріацію.
У матричній формі легко знайти дисперсії параметрів 30, 3ь- -, 3т та встановити коваріації між двома попарними їхніми значеннями, тобто між 3і та
З j при і Ф у. Ці значення утворюють дисперсійно-коваріаційну матрицю
М[(в - в) • (в - Р)'] =
/V /-Ч /V /V /V /V
М (30 - 30) М (30 - 30)(31 -31) ■■■ М (30 — 30)(3т — 3т )
/V /V /V г\ /V /V
= М(31 - 31)(30 - 30) М(31 - 31) ■■■ М(31 - 31 )(3т - 3т ) = . Матриця кореляції.
В економетричній моделі У = XP + и вектор и і залежний від нього вектор У є випадкові змінні. Оскільки в ми визначаємо з виразу в = (XX)-1X'У в який входить У, то в також можна вважати випадковою
функцією оцінювання параметрів моделі. Тому для характеристики в
необхідно знати не тільки математичне сподівання, а й дисперсію, коваріацію.
У матричній формі легко знайти дисперсії параметрів 30, 3ь- -, 3т та встановити коваріації між двома попарними їхніми значеннями, тобто між 3і та
З j при і Ф у. Ці значення утворюють дисперсійно-коваріаційну матрицю
М[(в - в) • (в - Р)'] =
/V /-Ч /V /V /V /V
М (30 - 30) М (30 - 30)(31 -31) ■■■ М (30 — 30)(3т — 3т )
/V /V /V г\ /V /V
= М(31 - 31)(30 - 30) М(31 - 31) ■■■ М(31 - 31 )(3т - 3т ) =
|












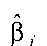



| або в матричному вигляді: |
| 6 2 = —: (3.21) п - т -1 |
| На головній діагоналі цієї матриці знаходяться дисперсії оцінок, а поза діагоналлю - коваріації оцінок. Позначається дисперсійно-коваріаційна матриця уаг(Р) і визначається за формулою: уагф) = с „2(X X)-1 (3.20) де с2 - оцінена дисперсія випадкової величини, яка визначається за формулою: П Те.2 |

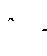
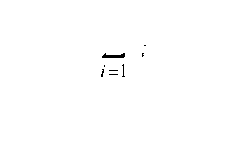
| 62 = УТ^СУ =. (3.21') п - т -1 п - т -1 |

 23. Перевірка адекватності прийнятої економетричної моделі реальній дійсності проводиться аналогічно лінійній моделі з однією пояснюючою змінною. Для цього користуються найчастіше критерієм Фішера (^—критерієм). Нульова гіпотеза має вигляд:
23. Перевірка адекватності прийнятої економетричної моделі реальній дійсності проводиться аналогічно лінійній моделі з однією пояснюючою змінною. Для цього користуються найчастіше критерієм Фішера (^—критерієм). Нульова гіпотеза має вигляд:
Н 0 : Р 0 = Ь1 = — = Р т = °.
 Альтернативна гіпотеза наступна:
Альтернативна гіпотеза наступна:
Н1: не всі Р у (] = 0, т) дорівнюють нулю.
 Я кщ о нульова гіпотеза відхиляється і приймається альтернативна гіпотеза, то це означає, що включені до моделі фактори пояснюють змінну у. Величина ^—відношення для багатофакторної моделі з т та п — т — 1
Я кщ о нульова гіпотеза відхиляється і приймається альтернативна гіпотеза, то це означає, що включені до моделі фактори пояснюють змінну у. Величина ^—відношення для багатофакторної моделі з т та п — т — 1

|
ступенями вільності наступна:
| де т - кількість факторів, що ввійшли в модель, п - кількість спостережень у вибірці. |
| Р =------------ т----------- =---------------------- і=1--------------, (3.26) пп Е( у і- р);)2 тЕ(Уі- у;)2 і=1____________________ і = 1 п - т -1 |
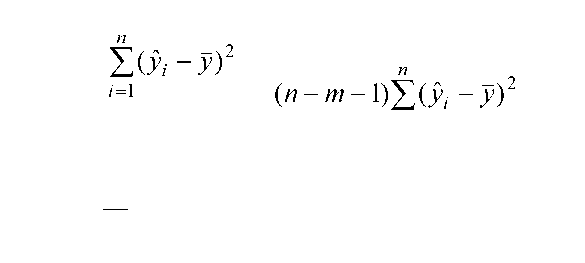


| Або якщо відоме значення коефіцієнта детермінації то Р-відношення таке: р = (п - т - 1>д2 (3.26') т(1 - Я2) Після обчислення ^-відношення Фішера знаходимо Екр(т;п - т -1;у), яке є критичним значенням Р при заданому рівні значущості у (або у-100%) та відповідно т і п - т -1 ступенях вільності. Якщо Р > Ркр, то ми відкидаємо Н0 з ризиком помилитися не більше ніж в у % випадків, і приймаємо, що побудоване рівняння економетричної моделі адекватне реальній дійсності. В протилежному випадку Р < Ркр - Н0 приймаємо і вважаємо, що побудована модель неадекватна. Тоді необхідно, можливо, будувати нелінійну модель або ввести додаткові фактори. |



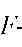







24. Для розгляду значущості оцінок параметрів розглядаються нульові гіпотези:

|

 Н0: Ь j = 0, тобто пояснююча змінна х]- не впливає суттєво на у.
Н0: Ь j = 0, тобто пояснююча змінна х]- не впливає суттєво на у.
Альтернативна - Н1: Ь j Ф 0, тобто пояснююча змінна Xj впливає суттєво
 на У.
на У.
 Емпіричне значення відношення tj для перевірки нульової гіпотези стосовно параметрів Ь j знаходиться за формулою:
Емпіричне значення відношення tj для перевірки нульової гіпотези стосовно параметрів Ь j знаходиться за формулою:
де 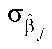 - стандартна похибка оцінки о з матриці
- стандартна похибка оцінки о з матриці
var(ß), яку знаходимо по формулі (3.20).
Емпіричне значення о цін ки 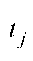 порівнюють з критичним, знайденим за таблицями Стьюдента, для заданого рівня значущості
порівнюють з критичним, знайденим за таблицями Стьюдента, для заданого рівня значущості 
 ступенів
ступенів
вільності. Якщо 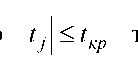 го гіпотеза про рівність нулю параметра
го гіпотеза про рівність нулю параметра  в
в
генеральній сукупності не відхиляється, оцінка 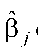 є статистично незначущою;
є статистично незначущою;
то із заданим рівнем значущості 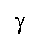 гіпотезу
гіпотезу  слід відхилити і
слід відхилити і
відповідну оцінку вважають статистично значущою.
Побудова довірчих інтервалів для параметрів 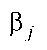 проходить аналогічно
проходить аналогічно
довірчим інтервалам параметрів рівняння економетричної моделі з двома змінними. Спочатку знаходимо граничні похибки оцінок за формулою




де 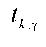 - імовірнісний коефіцієнт, який знаходиться за таблицями Стьюдента при рівні значущості
- імовірнісний коефіцієнт, який знаходиться за таблицями Стьюдента при рівні значущості 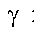 і ступенях вільност
і ступенях вільност 
Довірчий інтервал, в межах якого при заданому рівні значущості 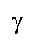 або надійності або надійності  міститься невідомий параметр міститься невідомий параметр 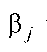 генеральної сукупності: генеральної сукупності:
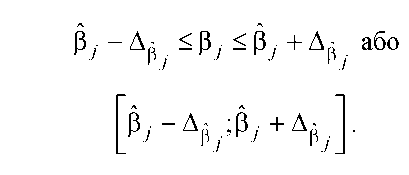
|






