Декартовим добутком двох множин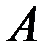 
і 
називається множина всіх пар 
,в якій елемент 
,елемент 
. 
.
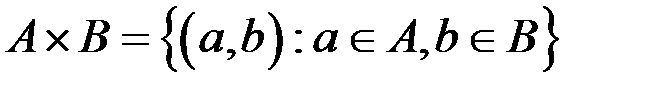Наприклад:
М={а,в,с}
N={1,2}
M*N={(а,1)(а,2)(в,1)(в.2)(с,1)(с,2) }
Операція декартового добутку не асоціативна та не комутативна M*N ≠N*M
Тотожності, які справещдливі для декартовоо добутку:АᴗВ*С=(А*С)ᴗ(В*С)
А∩В*С=(А*С)∩(В*С)
5.Відношення. Операції над відношеннями
відношення між елементами множин А та В називається будь-яка підмножина С≤А*В декартового добутку множин А*В.
С≤M*N
C={(a,1(,(b,1),(c,1)}
C={(a,b);aЄΜ,bЄB}
n-арним відношенням R на множинах Х1, Х2, ...,Хn називається підмножина декартового добутку цих множин.
Якщо n=1 при R≤xn, то відношення називається унарним.
Якщо n=2 при R≤xn, то відношення називається бінарним.
6.Бінарні відношення та їх власт. Сеперпозиція відношень.
Бінарне відношення — відношення на множині, яке встановлюється між двома елементами множини.
Іноді розрізняють поняття бінарного відношення на множині та бінарного відношення між множинами, яке називається відповідністю між множинами.
Властивості:
1. Рефлексивність ( a,b) 
R, aRb.
Відношення R на множині x називається рефлексивним, якщо для будь-якого х що належать множині х (х Х) має місце 
, тобто кожний елемент х знаходиться у відношенні R до самого себе.
2. Антирефлексивність
Відношення R на множині х називається анти рефлексивним якщо з 
випливає, що 
3. Симетричність
Відношення R на множині х називається симетричним якщо для будь-якої пари з того що 
випливає те, що 
.
4. Антисиметричність
Відношення R називається антисиметричним якщо з того що якщ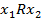о 
то випливає що 
5. Транзитивність
Відношення R на множині х називається транзитивним якщо 
випливає те що 
.
6. Антитранзитивність
Відношення R на множині х називається антитранзитивним якщо 
.
8. Відношення еквівалентності та його властивості. Теорема про розбиття. Фактор-множина
Відношення на множині називається відношенням еквівалентності, якщо воно задовольняє наступні властивості:
1) 
, 
2) Якщо 
і 
, то 
3) Якщо і 
, то 
для (
Теорема: Кожному відношенню еквівалентності на множинні М відповідає єдине розбиття даної множини на класи, і навпаки – кожне розбиття множини М одночасно задає відношення еквівалентності на множині М.
9.Відношення часткового порядку та його власт. Відношення кватіпорядку.
Відношення R на множині M називається відношення часткового порядку, якщо воно задовольняє властивості:
1. для будь-якого a є М, aRa - рефлективність
2. aRb і bRa, то a=b – антисиметричність
3. aRb і bRc, то aRc для a,b,c є M – транзитивність
За кожним відношенням часткового порядку ≤ на довільній множині М можна побудувати інше відношення < на М поклавши a<b тоді і тільки тоді коли a≤b і a≠b, це відношення називають відношенням строгого порядку на множині М.
10.Чатково впорядковані множини. Аксіома повної впорядкованості.
Частково впорядкованою множиною 
називається множина 
із заданим на ній рефлексивним, антисиметричним та транзитивним бінарним відношенням 
(називається — відношення нестрогого порядку).
Власт: рефлексивність: будь елемент не перевершує самого себе; антисиметричність: якщо 
не перевершує 
, а не перевершує , то елементи і збігаються; транзитивність: якщо не перевершує , а не перевершує 
, то не перевершує .
А ксіома повної упорядкованості. Всяку непусту множину можна повністю впорядкувати.
11. Метод трансфінітної індукції
Трансфінітна індукція — метод доведення, що узагальнює математичну індукцію у випадку незліченного числа значень параметра.
Нехай e – найменший елемент повністю впорядкованої множини A і P(x) – деяка властивість елемента x∈A. Тоді якщо із істинності P(e) і P(x) для всіх x<a випливає істинність P(a), то P(x) істинно для всіх x із A.
Існують нескінченні множини, елементи яких не можна перенумерувати. Такі множини називають незліченними.
12: Відображення. Аксіома вибору.
Аксіома вибору. Якщо X – об’єднання непорожніх множин Хi, що не перетинаються, то існує щонайменше одна підмножина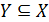 
, перетини якої з кожною множиною Хi одноелементні.
Нехай Х – множина відправлення функціональної відповідності f, Y – множина її прибуття, А – область її визначення. Якщо А=Х, тобто область визначення функції f співпадає з множиною її прибуття, то кажуть, що задано відображення f множини Х в множину Y. Іншими словами, відображенням f множини Х в множину Y називають таку відповідність між множинами Х і Y, при якій кожному елементу 
Х відповідає єдиний елемент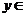 
Y.
13. Елементарна класифікація відображень.
Всюди визначена функціональна відповідність f⊆A×B називається відображенням з A в B і записується як і функція f:A→B або A→ B. Відображення називають також усюди або скрізь визначеними функціями.
Відображення типу A→A називають перетвореннями множини A. Через 
позначається множина всіх відображень з A в B. Оскільки функція і відображення є окремими випадками відповідності, то для них мають місце всі наведені вище означення: поняття областей визначення та значень, поняття образу та прообразу елементів і множин тощо. Зокрема, для функції f елементи множини Pr, f називають аргументами функції, образ f(a) елемента a∈Pr f називають значенням функції f на a. Відповідність C називається сюр’єктивною відповідністю на множину B, якщо Pr C =B. Відповідність C називається ін’єктивною, або різнозначною відповідністю, якщо для кожного елемента b∈ 
його прообраз 
складається тільки з одного елемента, різним елементам множини A відповідають різні елементи множини B.
Відображення, яке є одночасно сюр*активним та ін.*активним називається бієктикним або бієкцією. Бієктивні відображення називають часто також взаємно однозначними відповідностями між множинами А і В.
Таким чином, відповідність є взаємно однозначною тоді і тільки тоді, коли вона функціональна, всюди визначена сюр*активна та ін.*активна.
14.Композиція відображення. Обернене відображення.
Нехай задано відображення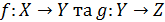 
. Тоді композицією відображення f і g будемо назив. відображення з множ. Х в множ. Z, визначене виразом 
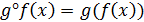для всіх елементів х з множ. Х. Композиції 
треба починати з відображення f.
Для відображення 
обернене відображення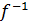 
тоді коли відображення f бієктивне (взаємно однозначне відображення множ. А на множ. В)
15.Потужність множини. Власт.
Потужність множини – це характеристика множ., що узагальнює поняття к-ті елем.множини.
Між двома скінченими множ. існує взаємно однозначна відповідність тоді коли їхні потужності збігаються.
Власт:
Дві скінченні множ. рівно потужні тоді коли вони скл. з однакового числа елем.
Скінченна множ. не еквівалентна жодній власні підмножині.
16. Зліченні множ. та їх власт.
Зліченні множини - це найменший клас потужності нескінченних множин.
Потужність зліченної множини називається потужність множини натуральних чисел.Зліченною називаються будь-яку множину рівнопотужні множині натуральних чисел.
Власт:
Всяка нескінченна підмножина зліченної множини зліченна. Обєднання зліченної кількості злічених множин є множина злічена. Обєднання зліченної кількості зліченних множин є множина зліченна.
17.Нескінченна множ. Теорема Кантора.
Незліченною мн-ною називається нескінчена мн-на, яка не є зліченою.
Теорема Кантора. Множина на всіх дійсних чисел з інтервалу (0,1) є незліченою множиною.
Теорема Кантора 2. Нехай М — нескінчена мн-на, а мн-на А є зліченною або скінченною підмножиною мн-ни М, то М\А~М (рівнопотужні).
18. Порівняння потужностей не скін. множ.. В загальному випадку, справедливому і для нескінченних множин, множини A та B є рівнопотужні, або мають однакову потужність, якщо можна встановити взаємно однозначну відповідність між елементами цих множин, тобто якщо існує бієкція f: A → B.
Рівнопотужні множини позначаються як A ~ B.
Відношення рівнопотужності є рефлексивним, симетричним та транзитивним, тобто є відношенням еквівалентності
Для нескінченних множин потужність множини може збігатися з потужністю її власної підмножини.
19. Основні принципи комбінаторики: правило суми та правило множення.
У багатьох практичних випадках виникає необхідність підрахунку кількості можливих комбінацій об’єктів, які задовольняють певні властивості, такі задачі називають комбінаторними.
Правило суми: Якщо об’єкт «х» можна вибрати n1 способами, а інший об’єкт «у» - n2 способами, то можна вибрати або «х», або «у» (n1+ n2) способами.
Правило добутку: Якщо об’єкт «х» можна вибрати n1 способами та після кожного такого вибору об'єкт «у» можна вибрати n2 способами, то пару об’єктів «ху» у зазначеному порядку можна вибрати (n1* n2) способами.
20. Комбінації. Число комбінацій з повтореннями та без.
Комбінація, сполука це спосіб вибору декількох речей з більшої групи, де (на відміну від розміщення) порядок не має значення.
Число різних m-елементних підмножин n-елементної множини становить
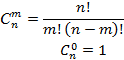
Число 
називається числом комбінацій або сполучень із n елементів по m елементів
Комбiнацiї без повторень — це сполуки, якi мають такi характернi ознаки:
1. Елементи у сполуцi не повторюються.
2. Кiлькiсть мiсць (m) у сполуцi не бiльша нiж кiлькiсть елементiв (n), якi претендують на цi мiсця (m ≤ n).
3. Порядок розташування елементiв у сполуцi не має значення.
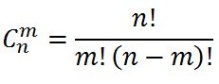
Комбiнацiї з повтореннями — це сполуки, якi мають такi характернi ознаки:
1. Порядок розташування елементiв у сполуках не має значення.
2. Елементи у сполуках можуть бути задiянi вiд нуля до m разiв: 0 ≤ ki ≤ m, де
§ m — кiлькiсть мiсць у кожнiй сполуцi вибраної групи;
§ ki — кiлькiсть мiсць у сполуцi для будь-якого елемента, що задiяний для її складання.
Кiлькiсть комбiнацiй з повтореннями обчислюють за формулою
21.Перестановки. Число перестановок з повторенням і без.
Перестановкою або підстановкою скінченної множини 
називається довільна бієктивна функція 
. Всього існує 
різних перестановок.
Перестановкою без повторень з даних n елементів даної n елементної множини М називають розміщення без повторень із даних n елементів по n елементів.
число перестановок із даних n елементів обчислюють за формулою: Рn=n!
Будь-яка довжина k, де k=k1+k2+k3+...+kn над даною n елементною множиною М, в якому елемент a1 - повторюється k1 раз, елемент a2 повторюється k2 раз, елемент a3 - k3 раз, … елемент an - kn разів називається перестановкою довжини k (k=k1+k2+k3+...+kn) з повтореннями.
Числом перестановок з перетвореннями обчислюють за формулою: Pk1,k2,k3,…kn =(k1+k2+k3+...+kn)!/(k1!k2!k3!...kn!).
22.Розміщення. Число розміщень з повторенням і без. Розміщенням із n елементів по m, або впорядкованою (n, m) вибіркою із множини M називають довільний кортеж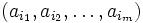 
що складається із m попарно відмінних елементів. Розміщення можна розглядати як різнозначну функцію f: 
, для якої 
.Кількість розміщень із n по m позначається як 
або 
і обчислюється за такою формулою:
Розміщенням з повтореннями із n елементів по m або впорядкованою (n, m) вибіркою з поверненнями називається довільний кортеж 
елементів множини M, для якого | M | = n.
Кількість можливих розміщень з повтореннями із n елементів по m дорівнює n піднесене до степеня m:
23. Біном Ньютона. Його властивості.
Біно́м Ньютона — вираз вигляду (a+b)n. Біном розкладається в суму одночленів, які є добутками деяких степенів його доданків a і b.
Спробуємо розкласти (a+b)n в многочлен у загальному випадку n. Запишемо його у вигляді добутку, пронумерувавши дужки:
Кожний доданок містить n множників: k множників a і (n-k) множників b, тобто має вигляд akbn-k, де k≤n, k≥0. Кожний такий доданок взаємно однозначно відповідає підмножині номерів дужок, з яких для утворення цього доданка, бралися множники a. Таким чином, доданків 
рівно стільки, скільки таких підмножин. В комбінаториці це число називається числом комбінацій з n по k і позначається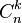 
.Отже,
Коефіцієнти при називаються біноміальними, оскільки записуються в розкладі бінома (a+b)n.
Біноміальні коефіцієнти мають очевидну властивість симетрії:
Розглянемо окремі випадки бінома Ньютона:
· при b=1 маємо: 
,
· при a=b=1 маємо: 
,
· при a= −1, b=1 маємо: 
.
Запишемо біноміальні коефіцієнти для початкових значень n=0, 1, …, 5 у трикутник Паскаля:
З таблиці видно, що кожний елемент, який не є першим у своєму рядку, є сумою елемента над ним і елемента, розташованого над ним і ліворуч:
.
Доведення цього факту можливе методом математичної індукції.
- у випадку 2-х множин
-у випадку 3-х множин
25. Метод рекурентних співвідношень.
Метод рекурентних співвідношень, дозволяє знаходити значення деякої функції для заданої величини аргументу через менші значення аргументів. Стосовно комбінаторики цей метод дає можливість знаходити розв'язок комбінаторної задачі для n предметів через розв'язок аналогічної задачі з меншим числом предметів за допомогою деякого співвідношення, яке називається рекурентним співвідношенням. Метод рекурентних співвідношень добре відомий з курсу шкільної математики, де він застосовувався при визначенні сума арифметичної і геометричної прогресій та при визначенні n-го члена цих прогресій.
24. Поліноміальна формула та метод продуктивних(твірних) функці
(а1 +а2+....+аk)=∑Рn(r1,r2...rm)a1r1*a2 r2*akr m*r1+r2+...+rm=n
r1,rm≥0 – поліноміальна формула
В комбінаторних задачах на підрахунки числа об'єктів
при деяких обмеженнях шуканим розв'язком часто є деяка послідовність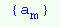 
, наприклад: при обчисленні числа розбиттів 
.
В цьому випадку послідовності можна поставити у відповідність формальний ряд
,
який називають твірною функцією послідовності 
. Функція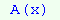 
може бути як функцією дійсної так і комплексної змінної. Вираз не що інше, як розклад функції 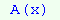в ряд Тейлора - Маклорена.
Для довільних рядів тa 
визначимо операції.
1. Додавання
2. Множення на число
3. Добуток Коші
де
27 Булева ф-я від одного та двох аргументів.
Булевою функцією від 1 аргументу називається функція f, задана на множині з двох елементів і набуваюча значення в тій же множині.
Булевою функцією від двох аргументів називається функція g задана на множині {0;1}x{0;1} і приймаюча значення в двохелементній множині {0;1}.
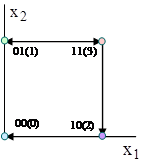
29. Наприклад, булеву функцію від двох змінних зображують на площині наступним чином. На рис. 12.1, б, вершини одиничного квадрата позначені довільними змінними. які утворюють кон’юнктивні терми на кожному двійковому наборі. Сусідні терми, що відрізняються тільки за однією координатою, склеюються уздовж з’єднуючого їх ребра, у результаті чого ребра позначаються спільною для вершин координатою.
| 
| ||
а б
Рисунок 12.1 – Геометрична інтерпретація довільної булевої функції від двох змінних: а – розташування двійкових наборів; б – позначення вершин і ребер
Для функції трьох змінних геометричне зображення виконують у вигляді куба, де вершини також позначаються десятковими цифрами, двійковими цифрами, довільними змінними. При цьому ребра куба поглинають вершини, а грані поглинають ребра (рис. 12.2).
Рисунок 12.2 – Склеювання вершин і ребер одиничного куба при геометричному зображенні булевої функції від трьох змінних
При геометричному зображенні булевої функції точками позначаються вершини, у яких дана функція приймає одиничні значення.
Приклад 12.4. Побудувати графік булевої функції 
.
|
Розв’язок. Щоб подати дану функцію геометрично, слід відмітити вершини куба з номерами 2,5,6 і 7, на яких досягаються одиничні значення функції (рис. 12.3).
Рисунок 12.3 – Геометрична інтерпретація функції 
У геометричному змісті кожний двійковий набір може розглядатися як
n-мірний двійковий вектор, що визначає точку n-мірного простору. Множина наборів, на яких визначена функція, подається у вигляді вершин n-мірного куба.
28.Теорема про булеві ф-ї з операціями Теорема де Моргана — властивість булевих алгебр, що дозволяє виразити одну з двоїстих операцій 
через іншу і унарну операцію 
доповнення (заперечення)
30. Теорема про Булеві функції пов’язані з операціями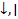 
. Стрілка Пірса — це двомісна логічна операція, яка є запереченням диз'юнкції; тому значення «істинно» одержується тільки тоді, коли обидва операнди мають значення «хибно». Іншими словами, функція приймає хибне значення, якщо хоча б один із аргументів істинний. 
Штрих Шеффера — двомісна логічна операція, яка є запереченням кон'юнкцїї; тому значення «хибно» одержується тоді й тільки тоді, коли обидва операнди мають значення «істина». 
.
31. Двоїстість булевих ф-й заданих за допомогою формул. Функцію f1(x1, x2, …, xn) називають двоїстою до функції f2(x1, x2, …, xn), якщо 
.В алгебрі Буля принцип двоїстості можна сформулювати так: для отримання формули F*, двоїстої до формули F, треба у формулі F всюди замінити 0 на 1; 1 на 0, ^ на v, v на ^
Якщо функція двоїста сама собі, тобто , її називають само двоїстою.
33. Теорема про представлення мулевих функцій через операції
Для кожної формули булевої функції A є рівносильна їй диз'юнктивна нормальна форма (ДНФ) і кон’юнктивна нормальна форма (КНФ).
Доведення теореми складається просто у вказівці алгоритмів знаходження для будь-якої формули A рівносильних їй ДНФ і КНФ. Процес знаходження цих форм називається приведенням формули A відповідно до ДНФ і КНФ. Для кожної формули A є, загалом кажучи, нескінченна множина ДНФ і КНФ, але для рішення задач, у яких ці форми потрібні, потрібно, як правило, знайти принаймні одну з них. ДНФ- називається формула що зображена у вигляді диз’юнкції елементарних кон’юнкцій КНФ- називається формула що зображена у вигляді кон’юнкції елементарних диз’юнкцій.
34.Функціонально повні системи булевих ф-й. Функціонально повною системою булевих функційназивається сукупність таких булевих функцій { f 1, f 2, …, fk }, що довільна булева функція f може бути записана у вигляді формули через функції цієї сукупності. Виходячи з визначення ДДНФ, ДКНФ, до функціонально повних систем булевих функцій слід віднести системы: 
.Перелічимо передповні класи булевих функцій: 1) булеві функції, які зберігають константу 0; 2) булеві функції, які зберігають константу 1; 3) самодвоїсті булеві функції; 4) лінійні булеві функції; 5) монотонні булеві функції.
35.Алгебра Жегалкіна. Теорема Жегалкіна.
Алгеброю Жегалкіна називається алгебра над множиною логічних функцій і змінних, сигнатура якої містить дві бінарні операції & і 
, і дві нульарні операції --константи 0 та 1.
Теорема Жегалкіна: стверджує існування і унікальність будь-якої булевої функції у вигляді поліному Жегалкіна. Формально поліном Жегалкіна можна представи
