В реальной жизни при реализации того или иного управленческого решения, в нашем случае оптимальной производственной программы, имеют место возмущения по параметрам системы, обусловленные внешними и внутренними факторами. Эти возмущения приводят к изменению оптимальных значений переменных задачи (объема производства продукции) и целевой функции (прибыли). Поэтому, возникает задача об оценке влияния этих возмущений на управленческое решение и на базе нее формулировки конкретных действий, которые лицо, принимающее решения, должно будет предпринять в этих условиях.
Для решения поставленной задачи будем использовать математический аппарат теории чувствительности.
Пусть мы находимся в классе задач линейного программирования:
(8)
где 
– параметры модели.
Предположим, найдено оптимальное решение задачи, то есть определены выходные характеристики задачи, а именно оптимальные значения переменных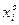 
и целевой функции 
. Продукцию, для которой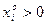 
, будем называть «выгодной»; продукцию, для которой 
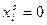- «невыгодной».
Введем в рассмотрение характеристику запасов ресурсов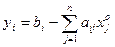 
, которая показывает количество ресурса 
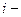ого вида, оставшегося после реализации оптимального решения.
Если 
, то ресурс будем называть «дефицитным». Если 
- ресурс «недефицитный».
Оценим влияние изменения запасов 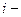ого ресурса на выходные характеристики задачи. Для этого введем в рассмотрение коэффициенты чувствительности 
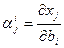, которые показывают, на сколько изменится значение 
ой переменной при увеличении запаса 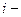ого ресурса на единицу. В теории чувствительности обосновано, что данные коэффициенты отличны от нуля для «дефицитных» ресурсов и равны нулю для «недефицитных».
Коэффициенты чувствительности 
, показывают, на сколько измениться значение целевой функции при увеличении запаса 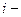ого ресурса на единицу.
Проведем анализ чувствительности решения к изменению параметров системы для периода t0+1. Пусть целевой функцией является максимизация прибыли, а ограничениями выступают запасы сырьевых ресурсов.
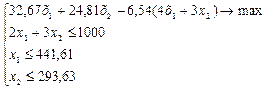(9)
Найдем оптимальный план:
Так как 
, следовательно и первая и вторая продукция «выгодные».
Определим резервы по ресурсам:
Отсюда делаем вывод, что первый и второй ресурс являются «дефицитными», третий - «недефицитный». Так как, коэффициенты чувствительности для «недефицитного» ресурса равны нулю, следовательно 
. Для определения оставшихся коэффициентов чувствительности, исключаем из системы ограничений третье неравенство, в двух других перейдем к строгим равенствам и обозначим правые части через 
и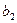 
. Получим:
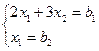(10)
Продифференцируем данную систему по :
(11)
или с учетом :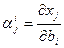
(12)
Откуда 
.
Аналогично, после дифференцирования системы по 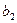, определим 
.
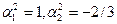Рассчитаем коэффициенты чувствительности целевой функции к вариациям «дефицитных» ресурсов.
Так как , следовательно
Предположим, что запас первого ресурса увеличился на 30 единиц. Как это повлияет на управленческое решение, а именно на оптимальную производственную программу и прибыль? Воспользуемся коэффициентами чувствительности 
и 
.
Так как 
, следовательно при увеличении запаса первого ресурса на 30 единиц, оптимальный объем производства первой продукции не изменится
Так как 
, следовательно, при увеличении запаса первого ресурса на 30 единиц, оптимальный объем производства второй продукции увеличится на 
единиц.
Так как коэффициент чувствительности 
, следовательно, при увеличении запаса первого ресурса на 30 единиц, максимальное значение прибыли увеличится на 
единиц.
Аналогично можно провести анализ чувствительности оптимального решения при изменении запасов по другим ресурсам.
