Анализ состояния и прогноз рыночной среды

Самара 2011

Реферат

Курсовой проект

Пояснительная записка: 42 с., 28 табл., 10 рис.

Спрос, предложение, производственные ресурсы, оптимальный объем производства, стратегическое планирование, оптимистический, пессимистический прогноз, линейная регрессия, максимизация прибыли, коэффициенты чувствительности, оценка устойчивости, инвестиционный проект, чистый дисконтированный доход, дополнительный доход, срок окупаемости

В курсовом проекте рассматривается задача управления деятельностью условной фирмы с учетом внешних и внутренних факторов. Моделируются процедуры принятия управленческих решений на различных этапах: анализ состояния, прогноз рыночной среды, оценка риска принятия решений, выбор оптимальных (рациональных) стратегий, прогноз достигаемых результатов. Отдельной частью курсового проекта является оценка целесообразности реализации инвестиционных проектов в условиях рыночного риска и неопределенности.

Содержание

 

Реферат.. 2

Введение.. 4

Задание.. 5

1 Постановка задачи.. 6

2 Анализ состояния и прогноз рыночной среды... 8

3 Расчет производственной программы деятельности предприятия.. 15

3.1 Расчет оптимальных производственных программ

с учетом стратегии развития.. 15

3.2 Оценка чувствительности результатов расчета оптимальной производственной программы 32

3.3 Оценка устойчивости управленческих решений.. 35

4 Принятие решений по реорганизации производства.. 38

Заключение. 41

Список литературы... 42

 

Введение

 

В данном курсовом проекте на примере задачи управления деятельностью условной фирмы с учетом факторов внешней среды моделируются процедуры принятия управленческих решений на различных этапах: анализ состояния, прогноз рыночной среды, оценка риска принятия решений, выбор оптимальных (рациональных) стратегий, прогноз достигаемых результатов. При выполнении курсового проекта применяются правила математической формализации задач принятия управленческих решений; изучаются методы снятия неопределенности при решении подобных задач; проводится моделирование изменения параметров системы во времени с помощью метода статистического прогнозирования; используются современные пакеты прикладных программ, ориентированные на решение подобного класса задач.

Важной частью курсового проекта является решение задачи по разработке оптимальной стратегии поведения предприятия в рыночных условиях, а также проведение анализа чувствительности результата управленческих решений к изменению внутренних и внешних факторов и оценка устойчивости управленческих решений.

Отдельной частью курсового проекта является анализ целесообразности реорганизации производства в условиях рыночного риска и неопределенности.

 

 

Задание

 

1. На основе содержательной постановки задачи провести ее математическую формализацию.

2. Используя статистическую информацию об изменении цены на первую и вторую продукции, цены на ресурс и объема продаж (спроса), построить уравнения регрессии первого порядка для каждого параметра. На основе уравнений регрессии рассчитать прогнозные значения исследуемых параметров на пять будущих периодов.

3. На основе математической постановки задачи, с учетом результатов прогноза изменения параметров системы, рассчитать оптимальные производственные программы предприятия по критерию максимизации прибыли.

3.1 Определить оптимальные объемы производства для оптимистического и пессимистического сценария развития событий.

3.2 Провести оценку чувствительности результатов расчета оптимальной производственной программы (для первого года при номинальных значениях параметров) и исследовать устойчивость опорного базиса системы.

3.3 Дайте графическую интерпретацию решения оптимизационной задачи (для одного года).

4. Определить срок окупаемости инвестиционного проекта по реорганизации производства.

 

Постановка задачи

 

Существует некоторая фирма, занимающаяся производством и выпуском двух видов продукции. Обозначим для определенности через и – количество выпускаемой продукции первого и второго типа, соответственно. При выпуске продукции используется два типа ресурсов – оборудование и сырье. Обозначим через полезный фонд времени работы оборудования. Известны нормативы затрат времени работы оборудования на производство единицы продукции и , которые показывают сколько времени необходимо затратить на изготовление единицы продукции первого и второго типа. Примем, что , , .

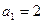Считается, что при производстве и первой, и второй продукции используется один вид сырьевого ресурса. Известны нормативы затрат сырьевого ресурса на производство единицы обоих видов продукции – и 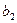. Принимаем, что , .

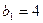Обозначим через и цену за единицу первой и второй продукции соответственно, через – стоимость единицы сырьевого ресурса.

Продукция, выпускаемая фирмой, характеризуется сложившимся на рынке объемом спроса. Пусть и – объем спроса на первую и вторую продукцию соответственно.

Цены реализации продукции и определяются ситуацией, которая складывается на рынке. К рассматриваемому моменту имеется ретроинформация (статистическая информация) о тенденциях изменения цен за предыдущие 10лет, которая качественно выглядит следующим образом:

 

Таблица 1 - Ретроинформация по цене на первую продукцию

Период времени ti	t0-10	t0-9	t0-8	t0-7	t0-6	t0-5	t0-4	t0-3	t0-2	t0-1	t0
Ц1		27,7	28,8	28,7	29,7	30,4	30,8	31,4	32,1	33,5	33,4

 

где t_i – это год. Тогда t_0-10 – это год начала рассматриваемого периода, а t₀ - текущий год.

 

Таблица 2 - Ретроинформация по цене на вторую продукцию

Период времени ti	t0-10	t0-9	t0-8	t0-7	t0-6	t0-5	t0-4	t0-3	t0-2	t0-1	t0
Ц2	18,4	18,7	19,3	19,9	20,8	21,1		22,5	22,5		23,8

 

Цена сырьевого ресурса Ц_р, приобретаемого для организации процесса производства, также формируется рынком.

Таблица 3 - Ретроинформация по цене на ресурс

Период времени ti	t0-10	t0-9	t0-8	t0-7	t0-6	t0-5	t0-4	t0-3	t0-2	t0-1	t0
Цр	5,3	5,6		5,8	5,9	6,4	6,5	6,5	7,1	6,5	6,5

 

Производство и реализация. Производственные возможности фирмы с учетом ограничения по полезному фонду времени работы оборудования можно графически представить следующим образом:

Рисунок 1 – Производственные возможности фирмы

 

Выбор производственной программы, т.е. значений Х₁ и Х₂, ограничиваются не только производственными возможностями, но и объемом практического сбыта этой продукции на рынке. Объем сбыта продукции определяется величиной спроса и . Примем, что фирма в прошедшие периоды производила продукцию в объеме равном величине спроса.

 

Таблица 4 - Ретроинформация по объему продаж (спроса) первой продукции

 

Период времени ti	t0-10	t0-9	t0-8	t0-7	t0-6	t0-5	t0-4	t0-3	t0-2	t0-1	t0

 

Таблица 5 - Ретроинформация по объему продаж (спроса) второй продукции

Период времени ti	t0-10	t0-9	t0-8	t0-7	t0-6	t0-5	t0-4	t0-3	t0-2	t0-1	t0

С учетом сказанного, необходимо определить стратегию поведения фирмы (определить оптимальный объем производства первой и второй продукции), по критерию максимизации прибыли предприятия на последующие пять лет.

Анализ состояния и прогноз рыночной среды

 

Для решения поставленной задачи на первом этапе необходимо осуществить стратегическое планирование, которое подразумевает выработку стратегии поведения на следующие пять периодов функционирования фирмы, т.е. на периоды t₀₊₁, t₀₊₂, t₀₊₃, t₀₊₄, t₀₊₅. При этом необходимо дать прогноз относительно изменения цены на продукцию обоих видов, цены на ресурс и объемов продаж, которые можно будет реализовать на рынке. Стратегическое планирование или прогнозирование основывается на ретроинформации (статистики) об изменении исследуемых параметров в прошедшие периоды. Используя численные методы, необходимо получить уравнение регрессии, которое представляет собой функциональную зависимость некоторого параметра от времени. В нашем случае под параметром следует понимать цену на продукцию первого или второго вида, цену на ресурс, объем продаж первой или второй продукции. Для проведения дальнейших исследований в курсовом проекте принимается допущение, что возможно использовать регрессии первого порядка:

(1)

Для расчета числовых коэффициентов и целесообразнее и удобнее использовать стандартное приложение «Анализ данных» (меню «Сервис») пакета Excel.

Полученные уравнения регрессии позволяют дать прогноз изменения интересующих параметров, а именно цен на продукцию, цены на ресурс и объемов продаж первой и второй продукции, в зависимости от времени. Так как в постановке задачи, речь идет о стратегии поведения фирмы в течение следующих пяти лет, то исследование следует ограничить будущими пятью годами.

Любая математическая модель, каковой является и уравнение регрессии, характеризуется некоторой погрешностью. Поэтому, необходимо по показателю среднеквадратического отклонения модели оценить погрешность прогноза и рассчитать пессимистический и оптимистический прогноз для исследуемого параметра. При этом под пессимистическим прогнозом будем понимать ситуацию, когда параметры задачи изменяются неблагоприятным для фирмы образом, а именно их изменение приведет к тому, что предприятие получит минимально возможную прибыль. Оптимистический прогноз является полной противоположностью пессимистического прогноза и рассчитывается для ситуации, в которой фирма получит максимально возможную прибыль.

Математическая модель расчета прогнозного параметра для оптимистического варианта имеет вид: (2)

где значение исследуемого параметра при оптимистическом прогнозе, 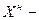номинальное прогнозное значение. Знак отражает содержательный смысл параметра. Речь идет о том, что некоторые параметры, такие как цены на выпускаемую продукцию или объем продаж, при своем увеличении приводят к росту прибыли предприятия. Напротив, цена на используемый ресурс только при своем уменьшении положительно сказывается на изменении прибыли. Поэтому выбор знака однозначно определяется содержательным и экономическим смыслом исследуемого параметра системы.

Математическая модель расчета прогнозного параметра для пессимистического варианта имеет вид:

(3)

где значение исследуемого параметра при пессимистическом прогнозе. Выбор знака также определяется содержательным смыслом прогнозируемого параметра.

Расчет прогнозных значений цены на первую и вторую продукцию, цены на ресурс, объемов продаж первой и второй продукции

 

Таблица 6 – Регрессионная модель для цены на первую продукцию.

Период	Цена реализации 1ой пр (у)	Порядковый номер величины в выборке Х1	Предсказанное у (уравнение регрессии у=27.51+0,43х)	Пессимистический прогноз	Оптимистический прогноз
t0-10			27,94
t0-9	27,7		28,37
t0-8	28,8		28,8
t0-7	28,7		29,23
t0-6	29,7		29,66
t0-5	30,4		30,3
t0-4	30,8		30,09
t0-3	31,4		30,52
t0-2	32,1		30,95
t0-1	33,5		31,38
t0	33,4		32,24
t0+1	33,3		32,67	30,49	34,85
t0+2	33,2		33,1	30,92	35,28
t0+3	33,1		33,53	31,35	35,71
t0+4			33,96	31,78	36,14
t0+5	32,9		34,39	32,21	36,57
Стандартное отклонение	2,176611211

 

 

Рисунок 2 - Регрессионный анализ данных по цене на первую продукцию

 

Таблица 7 - Регрессионная модель для цены на вторую продукцию

 

Периоды	Цена реализации 2ой пр (у)	Порядковый номер величины в выборке Х1	Предсказанное у (уравнение регрессии у=17.37+0.62х)	Пессимистический прогноз	Оптимистический прогноз
t0-10	18,4		17,99
t0-9	18,7		18,61
t0-8	19,3		19,23
t0-7	19,9		19,85
t0-6	20,8		20,47
t0-5	21,1		21,09
t0-4			21,71
t0-3	22,5		22,33
t0-2	22,5		22,95
t0-1			23,57
t0	23,8		24,19
t0+1	24,6		24,81	23,01	26,61
t0+2	25,4		25,43	23,63	27,23
t0+3	26,2		26,05	24,25	27,85
t0+4			26,67	24,87	28,47
t0+5	27,8		27,29	25,49	29,09
Стандартное отклонение	1,803884697

 

 

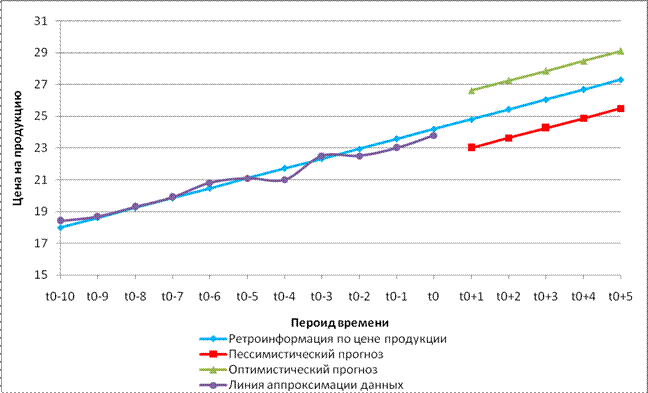
Рисунок 3 - Регрессионный анализ данных по цене на вторую продукцию

 

 

Таблица 8 - Регрессионная модель для цены на ресурс

Периоды	Цена реализации 2ой пр (у)	Порядковый номер величины в выборке Х1	Предсказанное у (уравнение регрессии у=5,7+0.07х)	Пессимистический прогноз	Оптимистический прогноз
t0-10	5,3		5,77
t0-9	5,6		5,84
t0-8			5,91
t0-7	5,8		5,98
t0-6	5,9		6,05
t0-5	6,4		6,12
t0-4	6,5		6,19
t0-3	6,5		6,26
t0-2	7,1		6,33
t0-1	6,5		6,4
t0	7,04		6,47
t0+1	7,2		6,54	7,06	6,02
t0+2	7,36		6,61	7,13	6,09
t0+3	7,52		6,68	7,2	6,16
t0+4	7,68		6,75	7,27	6,23
t0+5	7,84		6,82	7,34	6,3
Стандартное отклонение	0,516632452

 

Рисунок 4 - Регрессионный анализ данных по цене на ресурс

 

Таблица 9 - Регрессионная модель для объема продаж первой продукции

Периоды	Цена реализации 2ой пр (у)	Порядковый номер величины в выборке Х1	Предсказанное у (уравнение регрессии у=380,65+5.08х)	Пессимистический прогноз	Оптимистический прогноз
t0-10			385,73
t0-9			390,81
t0-8			395,89
t0-7			400,97
t0-6			406,05
t0-5			411,13
t0-4			416,21
t0-3			421,29
t0-2			426,37
t0-1			431,45
t0			436,53
t0+1			441,61	417,41	465,81
t0+2			446,69	422,49	470,89
t0+3			451,77	427,57	475,97
t0+4			456,85	432,65	481,05
t0+5			461,93	437,73	486,13
Стандартное отклонение	24,2005509

 

Рисунок 5 - Регрессионный анализ данных по объему выпуска первой продукции

 

Таблица 10 - Регрессионная модель для объема продаж второй продукции

Периоды	Цена реализации 2ой пр (у)	Порядковый номер величины в выборке Х1	Предсказанное у (уравнение регрессии у=181,55+9.34х)	Пессимистический прогноз	Оптимистический прогноз
t0-10			190,89
t0-9			200,23
t0-8			209,57
t0-7			218,91
t0-6			228,25
t0-5			237,59
t0-4			246,93
t0-3			256,27
t0-2			265,61
t0-1			274,95
t0			284,29
t0+1			293,63	262,18	325,08
t0+2			302,97	271,52	334,42
t0+3			312,31	280,86	343,76
t0+4			321,65	290,2	353,1
t0+5			330,99	299,54	362,44
Стандартное отклонение	31,451839

 

 

Рисунок 6 - Регрессионный анализ данных по объему выпуска второй продукции