Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщить в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении динамики изменений того или иного показателя ВЭД в разные периоды, в разных странах и т.д.
Обобщенной характеристикой ряда динамики служит прежде всего средний уровень ряда 
. Для разных видов рядов динамики он рассчитывается неодинаково. Ряды динамики бывают равномерные (с равными интервалами времени между уровнями), для которых средний уровень определяется по простой формуле средней величины, и неравномерные (с неравными интервалами), для которых используются формулы средних взвешенных (по интервалам времени) величин. В интервальном ряду динамики (в котором время задано в виде промежутков времени, к которым относятся уровни) определяется по формуле средней арифметической, а в моментном ряду (в котором время задано в виде конкретных моментов времени или дат, к которым относятся уровни) – по формуле средней хронологической. В табл. 29 приводятся виды рядов динамики и соответствующие формулы для расчета их среднего уровня .
Таблица 29. Виды средних величин, применяемых при расчете среднего уровня
| Вид ряда динамики | Название средней величины | Формула средней величины | Номер формулы |
| Равномерный интервальный | Арифметическая простая | 
| (82) |
| Равномерный моментный | Хронологическая простая |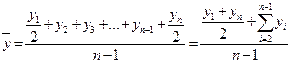 
| (83) |
| Неравномерный интервальный | Арифметическая взвешенная | 
| (84) |
| Неравномерный моментный | Хронологическая взвешенная |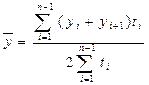 
| (85) |
В нашем примере про ВО России за период 2000-2006 гг. имеем равномерный интервальный ряд динамики, поэтому его средний уровень определяем по формуле (82):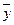 
= 1803,7/7 = 257,671, то есть ВО России в период 2000-2006 гг. составлял ежегодно в среднем 257,671 млрд. долл. США.
Кроме среднего уровня ряда рассчитываются и другие средние показатели:
– среднее абсолютное изменение (средний абсолютный прирост);
– среднее относительное изменение (средний темп роста);
– средний темп изменения (средний темп прироста).
Каждый из этих показателей может рассчитываться базисным и цепным способом.
Базисное среднее абсолютное изменение – это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (86); цепное среднее абсолютное изменение уровней ряда – это частное от деления суммы всех цепных абсолютных изменений на количество изменений (87):
Б = 
(86) Ц = 
(87)
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Очевидно, что числители формулы (86) и (87) равны между собой по формуле (76), значит, среднее абсолютное изменение не зависит от способа расчета (базисный или цепной), так как результат получится одинаковый. В нашей задаче по формуле (86) или (87):
= 318,5/6 = 53,083, то есть ежегодно в среднем ВО растет на 53,083 млрд. долл.
Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (88), а цепное среднее относительное изменение – по формуле (89):
Б= 
= 
(88) 
Ц= 
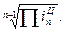(89)
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашем примере про ВО: = 
= 1,209, то есть ежегодно в среднем в период 2000-2006 гг. ВО России растет в 1,209 раза.
Вычитанием 100% из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашем примере про ВО: 
= 1,209 – 1 = 0,209, то есть ежегодно в среднем в период 2000-2006 гг. ВО России растет на 20,9%.
