Як було зазначено в п.9 в поперечних перерізах елементів конструкцій внаслідок дії зовнішніх сил виникають напруження ( та
та  ). В балках, обчислення нормальних та дотичних напружень виконують за формулами:
). В балках, обчислення нормальних та дотичних напружень виконують за формулами:
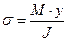 ,
,  (1)
(1)
де y – координата вздовж осі y, що визначає розташування точки визначення напруження;
 - момент інерції площі поперечного перерізу відносно центральної осі поперечного перерізу навколо якої діє момент М;
- момент інерції площі поперечного перерізу відносно центральної осі поперечного перерізу навколо якої діє момент М;
 - статичний момент площі частини поперечного перерізу, яка знаходиться вище координати y
- статичний момент площі частини поперечного перерізу, яка знаходиться вище координати y
d – ширина поперечного перерізу в місці визначення напруження.
Умова міцності балок за нормальними та дотичними напруженнями полягає в тому, що їх максимальні значення не повинні перевищувати допустимих:
 ,
,  . (2)
. (2)
При виникненні в коротких балках значних поперечних сил, виникає необхідність перевірки міцності за головними напруженнями. 3 теорія міцності має наступний вигляд:

Значення допустимих напружень залежать від типу матеріала конструкції та умов її експлуатації і визначаються за нормативною документацією. Як правило допустимі дотичні напруження приймають рівними  .
.
Якщо центральні осі розташовані симетрично до поперечного перерізу, обчислення максимальних нормальних напружень виконують за формулою:
 , (3)
, (3)
де 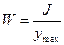 геометрична характеристика поперечного перерізу, що називається моментом опору. Формули обчислення W та J для поперечних перерізів у вигляді прямокутника та кола наведені в табл.1.
геометрична характеристика поперечного перерізу, що називається моментом опору. Формули обчислення W та J для поперечних перерізів у вигляді прямокутника та кола наведені в табл.1.
табл.1

|
 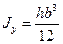
 
|

|


|
Дуже часто при розрахунках використовують стандартизовані поперечні перерізи у вигляді кутиків (а), швелерів (б), двотаврів (в), таврів (г на рис.39). Для них геометричні характеристики наведені в сортаменті. В табл.3 наведений фрагмент сортаменту для двотаврів.

а) б) в) г)
Рис.39
(4)
Приклад
Для балки зображеної на рис.36 необхідно підібрати таку конфігурацію поперечного перерізу у вигляді двотавра яка б забезпечувала її міцність за нормальними, дотичними та головними напруженнями. Балка має бути виготовленою зі сталі Ст.3 для якої:  ,
,  .
.
На першому етапі для визначення максимальних значень моментів та поперечних сил необхідно побудувати епюри внутрішніх зусиль. В п.10 показаний хід розрахунку цієї балки з побудовою зазначених епюр. Як можна побачити з епюр (рис.40):  ;
;  .
.
При виконанні розрахунку всі величини попередньо приведемо до системи СІ:
 ,
, 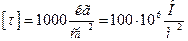
 ;
;  .
.
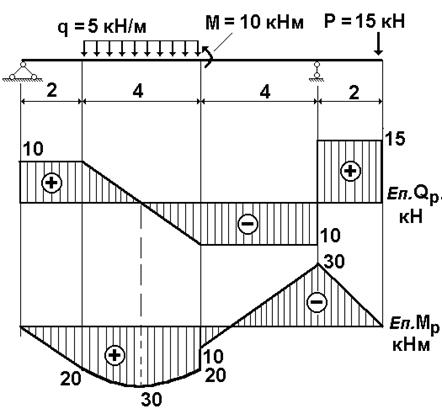
Рис. 40
За формулою (3) визначаємо потрібний момент опору для поперечного перерізу:

В табл.3 шукаємо двотавр для якого  . Таким є двотавр №20Б1 для якого:
. Таким є двотавр №20Б1 для якого:  ,
, 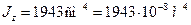 ,
, 
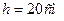 ,
,  ,
,  ,
,  .
.
Максимальні нормальні напруження виникають в крайніх точках двотавру (т.1 на рис.37,а), максимальні дотичні напруження діють в центрі двотавра (т.2 на рис.41,а).

а) б) в)
Рис. 41
Перевіряємо чи виконується умова міцності за нормальними та дотичними напруженнями в цих точках:
 ,
,
 .
.
Крім зазначених двох точок в двотаврах небезпечним також вважають місце поєднання стінки з поличкою (т.3 на рис.41,а). Тут міцність перевіряють за головними напруженнями. Оскільки еп.  є прямолінійною (рис.41,б), то значення нормального напруження в т.3 визначаємо використовуючи подібність трикутників:
є прямолінійною (рис.41,б), то значення нормального напруження в т.3 визначаємо використовуючи подібність трикутників:

Для обчислення дотичних напружень, попередньо визначимо статичний момент площі тієї частини двотавра що розташована вище від розглядуваної точки:

В якості величини d приймемо найменшу ширину перерізу в т.3:

Визначаємо значення дотичного напруження:
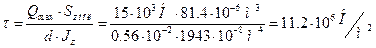
Обчислюємо головне напруження, та перевіряємо виконання умови міцності:

Отже міцність балки виконується за трьома умовами.
Визначення переміщень
Для визначення переміщень точок конструкції використовують формулу Мора:

При обчисленні переміщень для балок і плоских рам двома останніми складниками в наведеній формулі, внаслідок їх малості порівняно з першим, можна знехтувати:
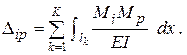
Для визначення переміщення за формулою Мора необхідно виконати наступне:
а) Побудувати епюру моментів в заданій схемі від дії зовнішнього навантаження. Такий стан називається вантажним (стан р). Епюра моментів позначається  ;
;
б) обрати одиничний стан конструкції (стан і) – звільнити конструкцію від заданих навантажень та завантажити її одиничним навантаженням, що діє в напрямку шуканого переміщення і прикладене в точці, переміщення якої визначається;
в) побудувати епюру моментів від одиничного навантаження ( );
);
г) обчислити переміщення за формулою Мора
Основні види переміщень і відповідні види одиничних навантажень наведені в табл.2.
Таблиця 2
| Переміщення | Одиничне навантаження |
| вертикальне переміщення точки А | 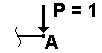
|
| горизотальне переміщення точки А | 
|
| кут повороту перерізу в точці А | 
|
| кут зламу в шарнирі в точці А | 
|
Інші види переміщень можуть бути отримані шляхом лінійних комбінацій вищеназваних випадків.
При обчисленні інтеграла Мора підсумовування виконується по окремих ділянках стержнів рами (k – номер ділянки, К – кількість ділянок інтегрування, lk – довжина ділянки). Кількість ділянок на кожному окремому стержні визначаємо виходячи із форми епюр 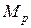 і
і  таким чином, щоб на ділянці лінія епюри моментів не мала зламів або стрибків. При сталій жорсткості стержня на згин обчислення інтеграла Мора
таким чином, щоб на ділянці лінія епюри моментів не мала зламів або стрибків. При сталій жорсткості стержня на згин обчислення інтеграла Мора  здійснюється за правилом Верещагіна або за формулою Корноухова–Сімпсона.
здійснюється за правилом Верещагіна або за формулою Корноухова–Сімпсона.
 Рис. 42. Метод Верещагіна
Рис. 42. Метод Верещагіна
| За правилом Верещагіна для обчислення інтеграла  необхідно помножити площу епюри необхідно помножити площу епюри  на ординату епюри на ординату епюри  , що береться під центром тяжіння епюри , що береться під центром тяжіння епюри  (рис.42): (рис.42):

| |
Якщо ордината  і площа і площа  розташовані по один і той самий бік стержня, добуток береться зі знаком “плюс”. розташовані по один і той самий бік стержня, добуток береться зі знаком “плюс”.
 Необхідно звернути увагу:
· принаймні одна з епюр, які перемножуються, має бути прямолінійною;
· ордината Необхідно звернути увагу:
· принаймні одна з епюр, які перемножуються, має бути прямолінійною;
· ордината  повинна бути взята на прямолінійній епюрі. повинна бути взята на прямолінійній епюрі.
| ||
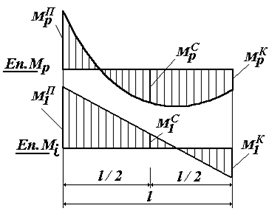 Рис. 43.Метод Сімпсона-Корноухова
Рис. 43.Метод Сімпсона-Корноухова
| В інших випадках, коли епюри мають більш складну форму, застосовуємо формулу Корноухова-Сімпсона (рис.43):
 де індекси "п","с","к" позначають відповідно початок, середину і кінець ділянки.
де індекси "п","с","к" позначають відповідно початок, середину і кінець ділянки.
| |
Якщо відповідні ординати на обох епюрах розташовані по один бік від стержня, перед їх добутком зберігається знак +, якщо по різні сторони стержня - ставиться наявність знаку "–" перед добутком  обумовлена розташуванням ординат епюр
обумовлена розташуванням ординат епюр  по різні сторони від вісі стержня.
по різні сторони від вісі стержня.
Приклад
Визначимо вертикальне переміщення т.К балки зображеної на рис.44,а. Балка виготовлена зі сталі Ст.3 для якої модуль пружності  , момент інерції відповідає поперечному перерізу у вигляді двотавра №20Б1
, момент інерції відповідає поперечному перерізу у вигляді двотавра №20Б1 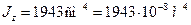 .
.
На першому етапі розраховуємо балку на зовнішні навантаження та будуємо епюру моментів  (рис.44,б). В п.11 показаний хід розрахунку цієї балки з побудовою зазначеної епюри. На наступному етапі обираємо одиничний стан балки (стан і) – звільняємо балку від заданих навантажень та завантажуємо її одиничною вертикальною силою, що діє в напрямку шуканого переміщення і прикладене в точці, переміщення якої визначається (рис.44,в). Знову виконуємо розрахунок балки на дію однієї одиничної сили і будуємо епюру моментів
(рис.44,б). В п.11 показаний хід розрахунку цієї балки з побудовою зазначеної епюри. На наступному етапі обираємо одиничний стан балки (стан і) – звільняємо балку від заданих навантажень та завантажуємо її одиничною вертикальною силою, що діє в напрямку шуканого переміщення і прикладене в точці, переміщення якої визначається (рис.44,в). Знову виконуємо розрахунок балки на дію однієї одиничної сили і будуємо епюру моментів  (рис.44,г). Для обчислення переміщення за формулою Мора необхідно епюри
(рис.44,г). Для обчислення переміщення за формулою Мора необхідно епюри  та
та  розбити на ділянки на яких немає зламів і не змінюється характер епюри. На еп.
розбити на ділянки на яких немає зламів і не змінюється характер епюри. На еп.  таких ділянок чотири, а на еп
таких ділянок чотири, а на еп  - три (на рис.44,б,г вони показані зверху над епюрами). Для визначення переміщення схеми розбивки двох епюр на ділянки мають бути однаковими. У зв’язку з цим І ділянку на епюрі еп
- три (на рис.44,б,г вони показані зверху над епюрами). Для визначення переміщення схеми розбивки двох епюр на ділянки мають бути однаковими. У зв’язку з цим І ділянку на епюрі еп  вимушено розбиваємо на дві ділянки. Оскільки на ІІІ ділянці еп
вимушено розбиваємо на дві ділянки. Оскільки на ІІІ ділянці еп  моменти мають нульові значення і результат перемноження епюр буде рівним нулю остаточно маємо по три ділянки на кожній з епюр (на рис.44,б,г вони показані знизу під епюрами). Для обчислення інтеграла Мора скористаємось методом Сімпсона-Карнаухова. Користуючись властивостями подібності трикутників на ділянках прямолінійних епюр визначаємо початкові, середні та кінцеві значення.
моменти мають нульові значення і результат перемноження епюр буде рівним нулю остаточно маємо по три ділянки на кожній з епюр (на рис.44,б,г вони показані знизу під епюрами). Для обчислення інтеграла Мора скористаємось методом Сімпсона-Карнаухова. Користуючись властивостями подібності трикутників на ділянках прямолінійних епюр визначаємо початкові, середні та кінцеві значення.
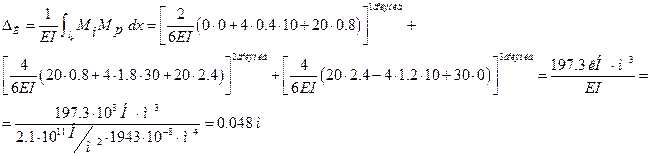

Рис.44






