Задачі механіки
Усі інженерні конструкції і споруди - будівлі, мости, башти, резервуари, корпуси машин, літаків, суден, ракет тощо - повинні задовольняти умовам міцності, жорсткості і стійкості.
Умови міцності полягають в тому, що внутрішні зусилля і напруження в елементах конструкцій не повинні перевищувати величин, за яких ці елементи можуть зруйнуватися.
В процесі експлуатації на конструкції і споруди діють зовнішні навантаження, внаслідок чого їхні елементи деформуються і набувають деяких переміщень у просторі. Ці переміщення можуть спотворити зовнішній вигляд споруди або взагалі зробити її непридатною до експлуатації. Перевірка умов жорсткості - це порівняння деформацій споруди з тими, що припускаються.
Отже при дії зовнішніх сил елементи конструкцій деформуються. При знятті цих навантажень споруда має поновлювати свій попередній стан. Це є умовою стійкості споруди. До цих умов слід ще додати умови економічності: споруда мусить відповідати умовам міцності, жорсткості і стійкості при забезпеченні її мінімальної вартості.
Виконання зазначених умов повинно передбачатися в процесі проектування конструкцій або споруд, тобто під час розрахунку їх на зовнішні дії і навантаження. Отже механіка розглядає методи розрахунку інженерних конструкцій і споруд на міцність, жорсткість і стійкість. Розділ механіки, в якому вивчаються загальні положення про сили та умови рівноваги тіл, називається статикою. В статиці розглядають дві основні задачі: приведення системи сил, що діє на тіло, до найпростішого вигляду та визначення умов рівноваги сил.
Основні термінологічні поняття
Сила — це фізична величина, яка визначає кількісну міру механічної взаємодії тіл. Сукупність сил, що діють на тіло, називається системою сил. Одиницею виміру сили в Міжнародній системі СІ є ньютон — Н. Відповідно тисяча ньютон називається кілоньютоном (1кН=1000Н), мільйон ньютон називають меганьютон (1МН=1000000Н).Сила є векторною величиною. На площині її визначають декілька параметрів: абсолютна величина (модуль), напрямок та точка прикладання. Дія будь якої сили  може бути представленою дією її проекцій (силами
може бути представленою дією її проекцій (силами 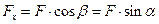 та
та  на рис.1) на відповідні осі прийнятої системи координат.
на рис.1) на відповідні осі прийнятої системи координат.
Рівновага — це стан спокою тіла по відношенню до інших тіл.
В'язями називають ідеалізовані пристрої та інші тіла, які утримують досліджуване тіло від певних переміщень.Сили взаємодії тіл, що виникають у в'язях, називаються реакціями.
Моментом сили 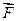 відносно точки А називається добуток величини сили на її плече відносно цієї точки, тобто на довжину перпендикуляру опущеного з цієї точки на лінію дії сили (рис.2).
відносно точки А називається добуток величини сили на її плече відносно цієї точки, тобто на довжину перпендикуляру опущеного з цієї точки на лінію дії сили (рис.2).
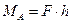
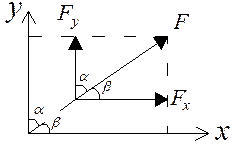
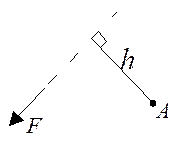
Рис.1 Рис.2
Якщо сила намагається обертати тіло відносно точки за годинниковою стрілкою, момент вважається додатнім, якщо проти годинникової стрілки (рис.2) – від’ємним.
Дві рівні за величиною і паралельні між собою сили, що спрямовані в протилежні сторони, утворюють пару сил.
Моментом пари сил називають добуток величини однієї із сил на відстань між ними. Якщо момент пари сил намагається повернути тіло за годинниковою стрілкою, він вважається додатнім.
Аксіоми статики
В основі статики лежить ряд аксіом, які узагальнюють життєвий досвід, численні експерименти та спостереження за рівновагою і рухом тіл.
Аксіома 1. Вільне абсолютно тверде тіло під дією двох сил може знаходитись у рівновазі лише тоді, коли ці сили мають однакові модулі, діють вздовж однієї прямої і мають протилежні напрями 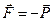 (рис. 3). Така система сил є зрівноваженою.
(рис. 3). Така система сил є зрівноваженою.
Під дією однієї сили тіло не може бути у рівновазі.
Аксіома 2. Дія заданої системи сил на абсолютно тверде тіло не зміниться, якщо до неї додати або від неї забрати зрівноважену систему сил.(Дія системи сил на рис.3 еквівалентна дії системи сил на рис.4)
Не змінюючи механічного стану тіла, силу можна переносити вздовж лінії дії.
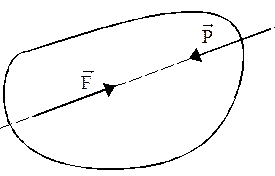
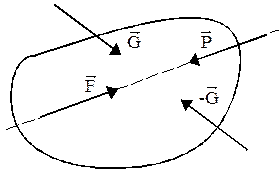
Рис.3 Рис.4
Аксіома 3. Система двох сил, прикладених до точки А, має рівнодійну, яка зображується діагоналлю паралелограма, побудованого на цих силах і має початок у точці А (рис.5).Ця аксіома ще називається додаванням векторів за правилом паралелограма
Аксіома 4. Сили взаємодії двох матеріальних тіл завжди рівні за модулем і протилежні за напрямом — дії завжди відповідає рівна і протилежна протидія.
Аксіома 5. Дію будь-якої в'язі на тіло можна замінити реакціями що в ній виникають (рис.6 ).
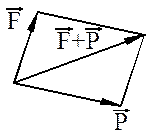

Рис.5 Рис.6
Типи в’язей
Кінематична в’язь що з’єднує два тіла (елемент С на рис.7,а), перешкоджає лінійному переміщенню одного тіла відносно другого у напрямку лінії в’язі, проте допускає взаємний поворот D1 тіл та взаємне поступальне переміщення D2 по нормалі до осі цієї в’язі.
У кінематичній в’язі виникає реакція R, лінія дії якої проходить вздовж осі в’язі. Способи позначення опорних стержнів наведені на рис.7,б
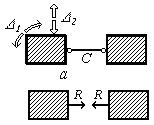
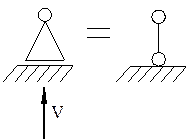
а) б)
Рис.7
Простий циліндричний шарнір (Ш на рис.8) що з’єднує два тіла, усуває можливість їх взаємних поступальних переміщень. Але він допускає їх взаємний поворот D відносно осі, яка проходить через центр шарніра. Реакція R (рис.8,б) у циліндричному шарнірі являє собою силу, яка проходить через його центр, але має заздалегідь невідомий напрямок, який може бути визначений в подальшому розрахунку. При аналітичному розрахунку її звичайно замінюють на дві непаралельні складові V і H, які зручно обрати взаємно ортогональними (рис.8,в). Способи позначення шарнірно-нерухомих опор наведені на рис.8,с
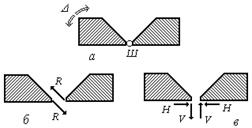

с)
Рис.8
Проста припайка (П на рис.9,а) повністю виключає взаємні лінійні та кутові переміщення двох тіл, які нею з’єднуються. Реакція в припайці складається з двох взаємно перпендикулярних сил V і H, а також моменту M (рис.9,в). Позначення жорсткого защемлення наведено на рис.9,б
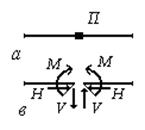

Рис.9 б)
Види навантажень
Навантаження поділяються на 3 типа:
1) Розподілені по довжині
2) Зосереджені (сила F на рис.10)
3) Пара сил (2 однакові за величиною але протилежні за напрямом сили Р розташованих на відстані а)
Розподілені навантаження безперервно діють на протязі певної довжини. Вони поділяються на рівномірно розподілені та нерівномірно розподілені. Величина рівномірно розподіленого навантаження, діючого на одиницю довжини тіла називається інтенсивністю навантаження і позначається 
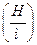 . При складанні рівнянь рівноваги визначають рівнодіючу розподіленого навантаження (Q). При дії рівномірно розподіленого навантаження з постійною інтенсивністю, рівнодіюча визначається за формулою:
. При складанні рівнянь рівноваги визначають рівнодіючу розподіленого навантаження (Q). При дії рівномірно розподіленого навантаження з постійною інтенсивністю, рівнодіюча визначається за формулою:
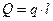
Точка прикладання рівнодіючої буде знаходитись посередині ділянки дії рівномірно розподіленого навантаження (рис.10,а)
Дуже часто на практиці замість завдання пари сил розглядають лише їх момент 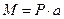 (рис.10,б).
(рис.10,б).
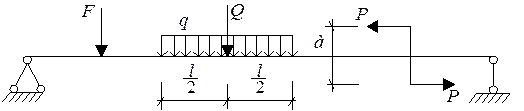
а)

б)
Рис.10
Визначення реакцій в’язей
Найбільш поширеним і загальним способом визначення реакцій є використання методу перерізів. Цей метод полягає в тому, що від споруди наскрізним перерізом, який проходить через з’єднання, відокремлюється якийсь її фрагмент (елемент, група елементів). Розрізані в’язі (з’єднання) відкидаються і замінюються силами - реакціями цих в’язей. Таким чином, на відокремлений фрагмент діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень і реакцій відкинутих в’язей. Визначення невідомих реакцій виконується виходячи з умов рівноваги які можна скласти для отриманої системи сил. Умови рівноваги плоскої системи сил виражаються трьома рівняннями:
1) Алгебраїчна сума проекцій всіх сил на будь-яку вісь прийнятої системи координат має дорівнювати нулю. Проекція сили вважається додатною, якщо її напрямок співпадає з напрямком вісі. При використанні декартової системи координат будемо мати два рівняння:
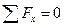 ,
, 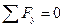
2) Алгебраїчна сума моментів всіх сил відносно довільної точки на площині має дорівнювати нулю
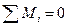
Приклад
Визначимо реакції у в’язях на схемі показаної на рис.11,а.
1) Використовуючи метод перерізів дію в’язей на схемі замінюємо дією реакцій, що можуть в них виникати. В шарнірно нерухомій опорі (т.А) можуть виникати горизонтальна (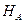 ) та вертикальна (
) та вертикальна ( ) реакції. В опорному стержні, що з’єднується із тілом в т.В, виникає одна реакція
) реакції. В опорному стержні, що з’єднується із тілом в т.В, виникає одна реакція  лінія дії якої проходить вздовж лініі стержня. Напрямки цих реакцій невідомі. Тому на початку задачі напрямок кожної реакції задаємо довільним чином. В результаті на вихідну схему діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень (q, F, пари сил P) і реакцій відкинутих в’язей (
лінія дії якої проходить вздовж лініі стержня. Напрямки цих реакцій невідомі. Тому на початку задачі напрямок кожної реакції задаємо довільним чином. В результаті на вихідну схему діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень (q, F, пари сил P) і реакцій відкинутих в’язей (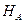 ,
,  ,
,  ) (рис.11,б).
) (рис.11,б).
2) Для подальших розрахунків замінимо дію рівномірно розподіленого навантаження, рівнодіючою силою 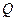 , а дію похилих сил
, а дію похилих сил  та F - їх проекціями на вісі декартової системи координат (рис.12,а):
та F - їх проекціями на вісі декартової системи координат (рис.12,а):
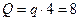 кН,
кН, 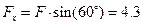 кН,
кН, 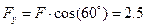 кН.
кН.

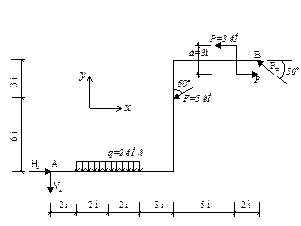
а) б)
Рис.11
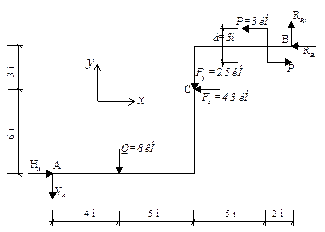
 а) б)
а) б)
Рис.12
Визначення невідомих реакцій будемо виконувати виходячи з умов рівноваги які можна скласти для отриманої системи сил. Спочатку візьмемо суму проекцій всіх сил на вісі x та y декартової системи координат:
1. 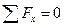


2. 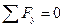

На основі отриманих рівнянь визначити реакції неможливо, оскільки в кожному з них по дві невідомих.
При складанні третього рівняння необхідно вибрати таку точку на площині, відносно якої лише одна з трьох невідомих реакцій (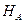 ,
,  ,
,  ) давала б момент. Для цього необхідно провести лініі дії всіх невідомих трьох реакцій і визначити точки в яких хоча б дві з них перетиналися (рис.12,б) В даній задачі таких точок є три (т.А,К,L). Зручніше з них взяти т.А оскільки її розташування на площині є відомим. Таким чином маємо рівняння з одним невідомим
) давала б момент. Для цього необхідно провести лініі дії всіх невідомих трьох реакцій і визначити точки в яких хоча б дві з них перетиналися (рис.12,б) В даній задачі таких точок є три (т.А,К,L). Зручніше з них взяти т.А оскільки її розташування на площині є відомим. Таким чином маємо рівняння з одним невідомим  .
.
 :
:
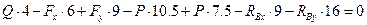

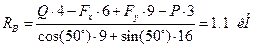
Визначивши  повертаємось до перших двох рівнянь і визначаємо
повертаємось до перших двох рівнянь і визначаємо 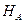 та
та  :
:
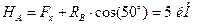 ,
,
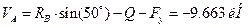 .
.
4) Після знаходження реакцій обов’язково необхідно виконати перевірку проведених розрахунків. Для цього необхідно додатково скласти ще одне рівняння рівноваги, незалежне від попередніх. Таким рівнянням може бути сума моментів всіх сил відносно будь-якої точки на площині, відносно якої знайдені реакції будуть давати ненульовий момент. Як можна побачити з рис.12 це може бути будь-яка точка, що не розташована на лініях дії реакцій. Для виконання перевірки візьмемо суму моментів відносно точки прикладання зосередженої сили F. Оскільки система повинна знаходитись в рівновазі, в результаті маємо отримати нуль.

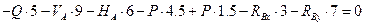
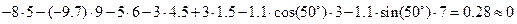
5) Після виконання перевірки встановлюємо дійсний напрямок обчислених реакцій. Якщо значення реакції вийшло додатним, то це означає що дійсний напрямок реакції співпадає з прийнятим на початку задачі. Якщо від’ємним – то дійсний напрямок є протилежним до прийнятого на початку задачі.
Як можна побачити з 1 та 2 рівнянь рівноваги пара сил не дає проекцій на вісі. ЇЇ дія виражається лише моментом 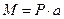 в 3 рівнянні. Тому в подальшому при розв’язанні інших задач пару сил будемо прикладати у вигляді момента, який відповідно не дає проекцій на вісі.
в 3 рівнянні. Тому в подальшому при розв’язанні інших задач пару сил будемо прикладати у вигляді момента, який відповідно не дає проекцій на вісі.
Розрахунок ферм
Фермою називається стержнева система, що складається із прямолінійних стержнів, які з’єднуються між собою у вузлах за допомогою наскрізних шарнірів.
Розглянемо основні терміни, які прийнято вживати щодо елементів ферми. Стержні ферми поділяються (рис.13) на верхній і нижній пояси та решітку. Решітка складається з похилих стержнів - розкосів та вертикальних - стояків. Розтягнуті стояки іноді називають підвісками. Стояки та розкоси, які розташовані біля опори, називають опорними.

Рис.13
Горизонтальна проекція відстані між опорами ферми l називається її прогоном. Горизонтальна проекція d відстані між суміжними вузлами верхнього або нижнього поясів називається відповідно верхньою або нижньою панеллю. Найбільша відстань h між вузлами верхнього і нижнього поясів називається висотою ферми.
Ферми вельми поширені в будівництві. Вони використовуються як основна несуча конструкція в покрівлях промислових і цивільних споруд великого прогону, підкранових балках, залізничних і автодорожніх мостах, потужних кранах тощо. Якщо на відокремлений від конструкції стержень з двома шарнірами на кінцях не діють зовнішні сили, він перебуває у стані рівноваги під дією двох сил взаємодії із залишеною частиною конструкції. Така система сил може бути зрівноваженою тільки в тому випадку, коли обидві сили розташовані на одній прямій. Отже, на не завантажений стержень ферми діють сили, спрямовані вздовж прямої, що з’єднує її кінці. Таким чином, у прямолінійних стержнях ферми, які не мають місцевого поперечного навантаження, можуть виникати лише поздовжні зусилля. Згинаючі моменти та поперечні сили відсутні.
При використанні ферми як несучого елемента споруди необхідно застосовувати конструктивні рішення, які передбачають навантаження ферм лише у вузлах, щоб уникнути дії місцевих сил на стержні. Тоді у стержнях виникають тільки притаманні ним поздовжні зусилля, що приводить до істотної економічності ферм порівняно з балками.
Розрахунок ферми полягає у визначенні зусиль в її стержнях.






