Векторное пространство. Основные теоремы

Векторное пространство – совокупность n-мерных в-в с действ. комп., рассм. с определенными в ней операциями сложения в-в и умножения в-ра на число.

Теорема1.

Любые S в-в n-мерного векторного пр-ва при S>n линейно зависимы.

Док-во:

а_{11 __} a_s1

: = α₁, …,: = α_s

а_1n a_sn

Док-ть, что существуют числа k₁, …, k_s одновременно неравные 0.

k₁α₁+…+ k_sα_s=0

а₁₁ a_s1 0

: k₁₊ …+: k_s =:

а_1n a_sn 0

k₁α₁₁+…+ k_sα_s1=0

…………………… – сист. лин. однород. урав с S неизв. k₁, …, k_s из n-уравнений

k₁α_1n+…+ k_sα_sn=0

Т.к. S>n, то сист. обладает ненулевыми решениями, т.к. числа k₁, …, k_s сущ.

Теорема2. __ __ __ __

В n-мерном пространстве (I) α₁,..., α_s (II) β₁, …, β_s

I лнз и линейно выраж через II, тогда r≤S

Док-во:

Предположим, что r>S

α₁=а₁₁β₁+…+а_1sβ_s

…………………

α_r=а_r1β₁+…+а_rsβ_s

S-мерные в-ры:

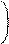
а_{11 __} a_r1 __ т.к. r>S, то по Теореме1 эти в-ры лз, т.е. сущ. такие числа, что

: = γ₁,…,: = γ_r k₁γ₁+…+ k_rγ_r=0

а_1s a_rs (k₁²+…+k_r²≠0)

а₁₁ a_r1 0

: k₁+…+: k_r =:

а_1s a_rs 0

Следствие1.

Любые 2-еэквивалентные лнз сист. сод. равное

число в-в.

Следствие2.

Любая макс и мин незав. сист. в-в n-мерного пр-ва сост. из n-в-в.

Число в-в, вход. в макс. лнз подсистему данной сист. в-в назыв. рангом сист. в-в.

Ранг матрицы. Теорема о ранге матрицы. Метод элементарных преобразований и метод окаймляющих миноров вычисления ранга матрицы.

Рангом матрицы назыв. макс число лнз столбцов.

Теорема о ранге матрицы.

Наивысший порядок, отличных от нуля миноров матрицы равен рангу этой матрицы.

А =

2 -4 3 1 0

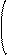
-1 -2 1 -4 2

0 1 -1 3 1

4 -7 4 -4 5

Методы вычисления ранга:

1) Метод элем. преобразования – находим минор 2 порядка, ≠0.

М₂¹= 2 -4 = 0 М₂²= -4 3 = 2 ≠ 0 rang A≥2

1 -2 -2 1

2) Метод окаймляющих миноров – находим минор 3 порядка, окаймляющей М₂² и ≠0.

Если таких нет, то rang А=2.

2 -4 3 2 -4 -1

М₃¹= 1 -2 1 = 1 -2 -1 = - 2 -1 = 1 ≠ 0. rang A≥3

0 1 -1 0 1 0 1 -1

3) Находим мино 4 пор., окайм. М₃¹ и ≠ 0.

 

2 -4 3 1 2 -4 -1 10 2 -1 10 2 1 12 _ 1 12

М₄¹ = 1 -2 1 -4 = 1 -2 -1 -1 = - 1 -1 -1 = - 1 0 0 = 1 12 = 0.

0 1 -1 3 0 1 0 0 4 -3 8 4 1 8

4 -7 4 -4 4 -7 -3 8 ^{+I +I}

^{+II +3III}

2 -4 3 0 2 -4 -1 4 2 -1 4 -II 1 0 0 _ -1 4

М₄² = 1 -2 1 2 = 1 -2 -1 4 = - 1 -1 -1 = - 1 -1 4 = -3 12 = 0. => rang A=3.

0 1 -1 1 0 1 0 0 4 -3 12 4 -3 12

4 -7 4 5 4 -7 -3 12

^{+II -II}

Следствие1.

Максимальное число лнз строк матрицы равно лнз столбцов.

Доказыв. с помощью транспониров.

Макс. пор. отлич. от нуля минора не измен., т.к. опред. не мен. при транспониров.

Теорема Кронекера-Капелли.

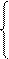а₁₁х₁+ а₁₂х₂+...+ а_1nх_n=b₁

а₂₁х₁+ а₂₂х₂+...+ а_2nх_n=b₂

………………………….

а_s1х₁+ а_s2х₂+...+ а_snх_n=b_s

a₁₁ ... a_{1n _ _} a₁₁ ... a_1n b­₁

A= …………, A=:::

a_s1 … a_sn a_s1 ... a_sn b­_s

^{основ. матрица сист. расширенная} __

Сист. совместна <=> rang осн. матрицы равен рангу расширенной(rang А = rang А)

Док-во:

1) Необх. =>

Пусть сист. совмечтна и числа k₁, …, k_n– одно из её реш., подставим эти числа в систе му вместо неизвест., мы получим S тождеств, показыв., что послед. столбец матрицы А линейно выражен через столбцы матрицы А.

2) Дост. <= __

Пусть ra ng A = rang A, тогда макс. лнз подсистема матрицы А и макс. лнз посистема матрицы А сод. равное число в-в и в кач. макс лнз подсист. А мы можем выбрать макс лнз подсист. из А. __

Через выбранную подсист. линейного выражения любой столбец матрицы А в том числе и последний столбец

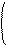
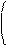а₁₁ a_1n b₁ что и означает, что числа k₁, …, k_n, явл. реш. сист., т.е. сист.

: k₁+…+: k_n =: совместна.

а_s1 a_sn b_s