Адаптивная оптимальная САУ на базе самоорганизующегося оптимального регулятора с экстраполяцией

 

Функциональная схема такой САУ (рис. 50) содержит следу­ющие элементы:

1. блок памяти;

2. блок оценивания;

3,7. исполнительные блоки;

4. экстраполятор нулевого порядка (ЦАП);

5. обобщенный объект регулирования (ОР);

6. блок автоматического поиска порядка математической мо­дели (ММ) объекта.

По принципу функционирования эта САУ относится к систе­мам с дискретным временем циклического типа. Входной вели­чиной самоорганизующегося оптимального регулятора с экстра­поляцией служит сигнал рассогласования х(t) между задающим воздействием g (t) и выходной

 

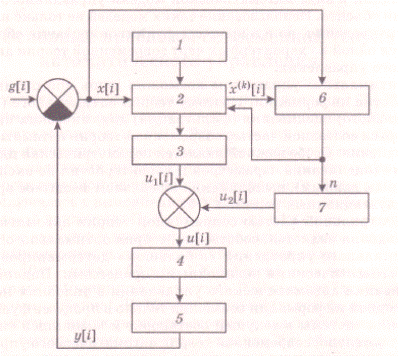
Рис.50

величиной y (t) объекта. Этот сиг­нал измеряется на каждом шаге, т. е. при t=iT, i= 0, 1, 2,….

В оперативной памяти 1 в табличном виде хранятся парамет­ры, определенные на стадии проектирования: значения элемен­тов матриц наблюдателей объекта с полиномиальной математи­ческой моделью различного порядка, оптимальные значения априорного времени экстраполяции и др.

В блоке оценивания 2 реализованы параллельно работающие рекуррентные циклические наблюдатели всех выбранных поряд­ков n = 2, 3,.., n_m. Полиномиальная математическая модель обобщенного регулируемого объекта эквивалентна цепочке по­следовательно соединенных интегрирующих звеньев, и блок 2 вы­рабатывает оценки векторов состояния этих цепочек для всех значений n. Соответственно каждый рекуррентный циклический наблюдатель строится по каскадной схеме, т. е. состоит из цепоч­ки последовательно соединенных наблюдателей Н _i (i = 1,..,, п) про­изводных (рис. 51, а), причем последние реализованы на базе фильтра Калмана-Бьюси второго порядка (рис. 51, б), у которого

 

Рис. 51

Помеха типа «белый шум» подавляется благодаря инерци­онности фильтра Калмана-Бьюси: первые оценки производных содержат «шум», а их вторые оценки - сглаженные, практически без «шума». Оценивание каждой последующей производной начинается после того, как завершится оценивание предыдущей (рекуррентный алгоритм). Так, например, после того, как и соответственно начинается оценивание и завершается при , в результате чего получается и т.д.

Для каждого фильтра Калмана-Бьюси коэффициенты k ₁ и k ₂ меняются во

Рис.52

времени в соответствии с передаточной функцией так, чтобы на начальном

этапе происходило оценивание наблюдаемой (входной) величины, а затем -

оценивание ее первой производной по времени (рис. 52).

В блок 6 (рис. 50) посылаются оценки для всех n, измеренные практически в один и тот же момент времени t благодаря малой затрате времени на оценивание (на порядок меньше периода наиболее высокочастотной составляющей движения объекта регулирования) и значительной инерционности объекта. По векторам оценок в этом блоке выполняется экстраполяция (т. е. предсказание, прогнозирование изменения) сигнала рассогласования на скользящий интервал для всех значений n, где Т_э – время экстраполяции.

Кроме того, в этот же блок поступают значения рассогласования 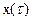и запоминаются на том же скользящем интервале. Далее осуществляется целочисленный поиск по п минимума усредненной нормы (например, квадрата) разности между фактическим и априорно предсказанным значением сигнала рассогласования. Это значение п считается оптимальным и по цепи местной ОС посылается в блок 2, а затем из этого блока в исполнительный блок 3. Кроме того, при этом происходит апостериорная оптимизация времени экстраполяции.

В исполнительном блоке 3 рассчитывается оптимальное управление u ₁ объектом на основе минимизации функционала обобщенной работы. В блоке 7 определяется дополнительное управление u ₂, компенсирующее неопределенности объекта. Управляющее воз­действие u = u₁ + u₂ после экстраполятора нулевого порядка име­ет вид кусочно-постоянной функции на интервалах , определяемой через рассогласование и оценки его производных. При этом могут быть реализованы астатизмы высокого порядка (v > 8), которые считались недостижимыми в эпоху аналоговой техники. Обобщенный объект 5 кроме ОР включает в себя усили­тели, приводы, измерительные преобразователи. На рис. 53 дана иллюстрация работы САУ и самоорганизующегося оптимально­го регулятора с экстраполяцией для ОР второго порядка.

Рис.53

Итак, данная САУ впервые позволяет реализовать адаптивное управление при неизвестной априори структуре ОР благодаря высокому уровню структурной и параметрической адаптации, которая обеспечивается прежде всего за счет применения наблю­дателей в виде фильтра Калмана-Бьюси, устройств экстраполя­ции и поиска порядка математической модели.

Как было указано, в этой САУ для оптимизации используется функционал обобщенной работы - неклассический функционал с аддитивными затратами как на синтезируемое управление u, так и управление u ₀ в оптимальной системе:

.

ОУ задан уравнениями с линейно входящими управлениями:

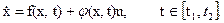
При аналитическом конструировании необходим синтез алго­ритма оптимального управления u ° = u °(х,t) на стадии проекти­рования, что наталкивается на существенные трудности. Более прост поиск u ⁰(t) САУ с прогнозирующей моделью в процессе работы системы.

Уравнение Беллмана для данной задачи имеет вид:

 

. (66)

Минимизация по u, т. е. дифференцирование по u и приравни­вание производной к 0, приводит к решению в неявном виде:

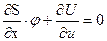. (67)

Подставляем (66) в (67) и учитываем дополнительное усло­вие, налагаемое на функции U и U *:

.

Данное условие означает, что левая часть этого неравенства должна быть положительно-определенной функцией относитель­но и, принимающей минимальное значение, равное 0 при u=u ⁰.

В результате получим уравнение в частных производных, на-
зываемое уравнением Ляпунова:

. (68)

Привлекая для решения этого уравнения метод характерис­тик, можно показать, что искомое решение строится на интег­ральных кривых, удовлетворяющих обыкновенным дифференци­альным уравнениям свободного движения объекта ():

(69)

где - вектор частных производных функций Беллмана S по компонентам вектора состояния.

Уравнение (69) может быть также получено из (68) непосред­ственным дифференцированием по x и изменением порядка дифференцирования.

Кроме того, при вычислении функции S (x,t) на свободной тра­ектории (u=0) из (68) вытекает уравнение

. (70)

Уравнения (69), и (70) составляют основу алгоритмов оптимизации с прогнозирующей моделью. Суть этих алгоритмов сводится к тому, что на основе интегрирования этих уравнений строится решение уравнения (68) и тем самым решается оптими­зационная задача. Упрощение состоит в том, что не требуется поиска структуры функции S (x,t) во всей области ее определе­ния, а требуется лишь вычисление ее значений в некоторой ок­рестности текущего состояния, достаточной для вычисления градиента , который затем используется в (67) для вычисления u ⁰(t).

 

Лекция 11.