Второй раздел курсовой работы посвящён особенностям постановки и решения некоторой разновидности общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП). Постановка и модель ТЗЛП представлена ниже:
Пусть имеется m пунктов отправления:
A1, A2,…Am, в которых сосредоточены запасы некоторых однородных грузов (товаров) в количестве a1,a2,…,am.
Имеется n пунктов назначения:
B1,B2,…,Bn, имеющих заявки на b1,b2,…,bn единиц грузов.
Предполагается, что сумма всех заявок равна сумме всех запасов:

Известна стоимость (Cij) перевозки единицы товара от каждого пункта отправления Ai до каждого пункта назначения Bj.
Матрица стоимостей выглядит следующим образом:

 C11 C12 Cn
C11 C12 Cn
C21 C22 C2n
…………………
Cm1 Cm2 Cmn
Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и общая стоимость перевозок была бы минимальная.
При такой постановке показателем эффективности плана является стоимость, поэтому задача называется транспортной по критерию стоимости.
Особенность задачи заключается в следующем:
Все коэффициенты при переменных в основных уравнениях задач равны 1.
А. Суммарное количество грузов должно быть равно запасу:
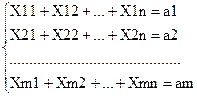 (2.1)
(2.1)
Б. Суммарное количество груза должно быть равно заявке:
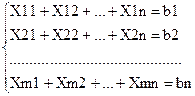 (2.2)
(2.2)
В. суммарная стоимость всех перевозок должна быть минимальна:
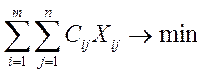 (2.3)
(2.3)
Г. Искомые переменные должны быть неотрицательными:
Хij³0 (2.4)
При выполнении второго раздела курсовой работы студенту следует составить модель ТЗЛП для своего варианта задания.
Автоматизированное решение ТЗЛП производится с помощью модуля «Поиск решения», работа с которым подробно описана в первом разделе настоящих методических указаний. Остановимся на некоторых особенностях решения ТЗЛП. На этапе ввода исходных данных в рабочей книге программы Excel рекомендуется создать две матрицы – для области изменяемых ячеек Xij и для области удельных затрат на доставку сырья Cjk (рисунок 2.1).
Клеткам матрицы изменяемых ячеек присваиваются единичные значения, данные для заполнения матрицы удельных затрат берутся из табл.5 приложения.
В поля С1:С3 и А3:А9 заносятся граничные значения объёмов спроса и предложения, взятые из условий задачи по вариантам задания.
Далее следует подготовить необходимые формулы, для чего:
· В ячейке I3:I9 с помощью встроенной функции СУММ ($C3:$G3) заносятся формулы для определения суммы по строкам матрицы изменяемых ячеек (объёмы предложения);
· В ячейки С12:П12 аналогичным способом заносятся формулы для вычисления сумм по столбцам матрицы изменяемых ячеек (объёмов спроса).
· В ячейку целевой функции С26 с помощью функции СУММПРОИЗВ заносится формула для вычисления целевой функции СУММПРОИЗВ (С3:G3; C17:G23).
Далее вызывается модуль «Поиск решения», в диалоговом окне которого задается адрес целевой ячейки, диапазон изменяемых ячеек и все виды ограничений в соответствии с моделью ТЗЛП.
При определении параметров поиска решения следует помнить, что оптимизация проводится по линейной модели с минимизацией значения целевой функции.
После успешного завершения работы модуля «Поиск решения» в области изменяемых ячеек С3:G9 рис.2.1. окажутся величины искомых переменных, т.е. оптимальные размеры поставок сырья от АО до филиалов предприятия, а данные отчетов по результатам, устойчивости и пределам предоставят студенту материал для дополнительного экономического анализа полученного оптимального решения.
| A | B | C | D | E | F | G | H | I | J | K | |
| Потребности филиалов | |||||||||||
| 16.4 | 18.4 | 16.2 | Bj | ||||||||
| Объем предложения | |||||||||||
| Аi | |||||||||||
| Объем спроса | |||||||||||
| 1,2 | 2,3 | 3,1 | 1,6 | 2,7 | Сij | ||||||
| 3,1 | 1,1 | 4,2 | 3,8 | 1,6 | |||||||
| 0,8 | 3,1 | 1,5 | 2,1 | 4,5 | Удельные затраты | ||||||
| 4,0 | 2,9 | 3,7 | 4,3 | 2,8 | |||||||
| 3,1 | 4,0 | 3,6 | 5,2 | 2,6 | |||||||
| 3,4 | 2,8 | 4,1 | 3,0 | 3,7 | |||||||
| 4,8 | 5,6 | 6,7 | 4,5 | 5,8 | |||||||
| Целевая ячейка - стоимость перевозки |
Рисунок 2.1. Образцы матриц и дополнительных полей для ввода исходных данных при решении ТЗЛП с помощью модуля “Поиск решения”






