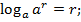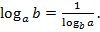Функція виду 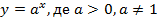 , називається показниковою (з основою
, називається показниковою (з основою  ).
).
Властивості показникової функції:
| а > 1 | 0 < а < 1 |
1. D(y) = R
2. Е(у) = (0; + 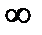 )
3. Зростає
x 1 > x 2 )
3. Зростає
x 1 > x 2 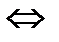  > >  4. Якщо х = 0, то у = 1
5. Якщо х < 0,то у < 1
6. Якщо х > 0, то у > 1
4. Якщо х = 0, то у = 1
5. Якщо х < 0,то у < 1
6. Якщо х > 0, то у > 1

| 1. D(y) = R
2. E(y) = (0; + 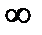 ).
3. Спадає
x 1 > x 2 ).
3. Спадає
x 1 > x 2 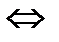  < <  4. Якщо х = 0, то у = 1
5. Якщо х < 0, то у > 1
6. Якщо х > 0, то у < 1
4. Якщо х = 0, то у = 1
5. Якщо х < 0, то у > 1
6. Якщо х > 0, то у < 1

|
14. Логарифм числа. Основні властивості логарифмів.
Рівняння ах = b, де a > 0, а ≠ 1, b > 0 має єдиний корінь. Цей корінь називається логарифмом числа b за основою a і позначається logab.
Логарифмом додатного числа  за основою
за основою  , де
, де  називається показник степеня, до якого треба піднести число
називається показник степеня, до якого треба піднести число  , щоб одержати число
, щоб одержати число  .
.
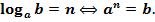

Вираз  де
де  має смисл лише при
має смисл лише при 
Якщо основа логарифма дорівнює 10, то логарифм числа називається десятковим логарифмом і позначається lg. 
Натуральним логарифмом називається логарифм за основою числа 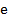 і позначається ln.
і позначається ln. 
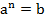 . Замінюючи в цій рівності
. Замінюючи в цій рівності  за означенням логарифма
за означенням логарифма  , дістанемо:
, дістанемо:
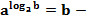 основна логарифмічна тотожність.
основна логарифмічна тотожність.
Основні властивості логарифмів:
Для будь – яких  і будь – яких додатних
і будь – яких додатних  виконуються рівності:
виконуються рівності:
15. Логарифмічна функція, її графік і властивості.
Функція виду  називається логарифмічною функцією.
називається логарифмічною функцією.
Властивості логарифмічної функції:
- Область визначення функції – множина всіх додатних чисел
 .
. - Область значень логарифмічної функції – множина R усіх дійсних чисел.
- Функція не є парною, ні непарною.
- Логарифмічна функція на всій області визначення зростає при
 , тобто
, тобто 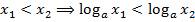 або спадає при
або спадає при  :
: 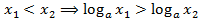 .
. - При
 значення функції дорівнює 0, тобто
значення функції дорівнює 0, тобто 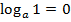 . Графік логарифмічної функції перетинає вісь Ох в точці (1;0).
. Графік логарифмічної функції перетинає вісь Ох в точці (1;0). - Якщо а > 1, то функція
 приймає додатні значення при х > 1, від'ємні — при 0 < х < 1. Якщо 0 < а < 1, то функція
приймає додатні значення при х > 1, від'ємні — при 0 < х < 1. Якщо 0 < а < 1, то функція  приймає додатні значення при 0 < х < 1, від'ємні — при х > 1.
приймає додатні значення при 0 < х < 1, від'ємні — при х > 1.
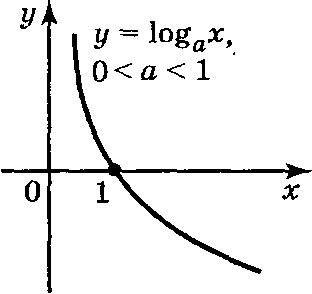

16. Похідна функції. Похідна алгебраїчної суми функцій. Похідна добутку двох функцій.
Похідною функції  в точці
в точці  називається границя відношення приросту функції
називається границя відношення приросту функції  до приросту аргументу
до приросту аргументу  за умови, що приріст аргументу
за умови, що приріст аргументу 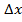 прямує до нуля, а границя існує
прямує до нуля, а границя існує

Функція, яка має похідну в точці  , називається диференційованою в точці
, називається диференційованою в точці  . Знаходження похідної називається диференціюванням.
. Знаходження похідної називається диференціюванням.
Похідна суми: Якщо функції  в точці
в точці 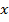 мають похідні, то функція
мають похідні, то функція
 в цій точці також має похідну, яка дорівнює
в цій точці також має похідну, яка дорівнює
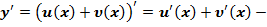
похідна суми дорівнює сумі похідних.
Наслідки. 1) похідна різниці дорівнює різниці похідних.
2) похідна суми декількох функцій дорівнює сумі похідних цих функцій.
Похідна добутку: Якщо функції  диференційовані в точці
диференційовані в точці 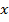 , то їхній добуток також диференційована функція в цій точці і
, то їхній добуток також диференційована функція в цій точці і
 .
.
Наслідок. постійний множник можна виносити за знак похідної.
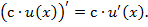
17. Похідна функції. Похідна частки двох функцій.
Похідною функції  в точці
в точці  називається границя відношення приросту функції
називається границя відношення приросту функції  до приросту аргументу
до приросту аргументу  за умови, що приріст аргументу
за умови, що приріст аргументу 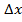 прямує до нуля, а границя існує
прямує до нуля, а границя існує

Функція, яка має похідну в точці  , називається диференційованою в точці
, називається диференційованою в точці  . Знаходження похідної називається диференціюванням.
. Знаходження похідної називається диференціюванням.
Теорема (похідна частки): Якщо функції  диференційовані в точці
диференційовані в точці 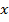 і
і
 то функція
то функція  також диференційована в цій точці і
також диференційована в цій точці і
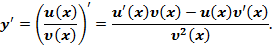
18. Похідна функції. Похідні показникової і логарифмічної функцій.
Похідною функції  в точці
в точці  називається границя відношення приросту функції
називається границя відношення приросту функції  до приросту аргументу
до приросту аргументу  за умови, що приріст аргументу
за умови, що приріст аргументу 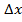 прямує до нуля, а границя існує
прямує до нуля, а границя існує

Функція, яка має похідну в точці  , називається диференційованою в точці
, називається диференційованою в точці  . Знаходження похідної називається диференціюванням.
. Знаходження похідної називається диференціюванням.
Похідна функції ex дорівнює самій функції:
(еx)’ = еx.
Знайдемо похідну функції f(x) = ax, скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:  Отже,
Отже,
 .
.
Розглянемо функцію у = ln x. За основною логарифмічною тотожністю: 
для всіх додатних х.
Диференціюючи обидві частини цієї рівності, одержимо:
 ,
,  .
.  .
.


Знайдемо похідну функції у = logаx. Так як loga х =  , то
, то 
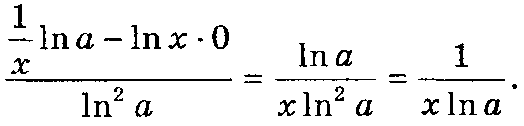


19. Похідна функції. Похідні тригонометричних функцій.
Похідною функції  в точці
в точці  називається границя відношення приросту функції
називається границя відношення приросту функції  до приросту аргументу
до приросту аргументу  за умови, що приріст аргументу
за умови, що приріст аргументу 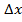 прямує до нуля, а границя існує
прямує до нуля, а границя існує

Функція, яка має похідну в точці  , називається диференційованою в точці
, називається диференційованою в точці  . Знаходження похідної називається диференціюванням.
. Знаходження похідної називається диференціюванням.
Знайдемо похідну функції  .
.
Надамо 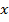 довільного приросту
довільного приросту  .
.
Тоді функція дістане приріст  .
.
Знайдемо відношення: 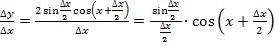 .
.
Перейдемо у цій рівності до границі, коли  :
:

 .
.
Отже, 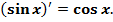
Аналогічно можна довести, що 
Знайдемо похідну функції 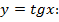

Отже, 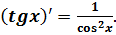
Аналогічно можна довести, що 
Похідні обернених тригонометричних функцій:



 .
.
20. Геометричний та механічний зміст похідної. Рівняння дотичної до графіка функції.
Геометричний зміст похідної:
Значення похідної функції у = f(x) в точці xo дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою xo: f'(xo) = k = tg α.
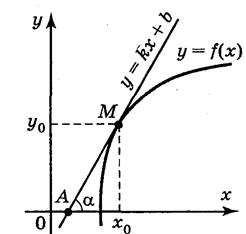
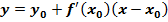 - рівняння дотичної до кривої у = f(x) в точці М(xo; уo).
- рівняння дотичної до кривої у = f(x) в точці М(xo; уo).
Нехай тіло рухається прямолінійно із змінною швидкістю по закону  , де
, де  – відстань, пройдена тілом за час
– відстань, пройдена тілом за час  .
.
Фізичний зміст похідної:
Швидкість руху точки в даний момент часу дорівнює значенню похідної від закону руху.
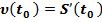
21. Екстремальні точки. Дослідження функції на екстремум за допомогою першої похідної.

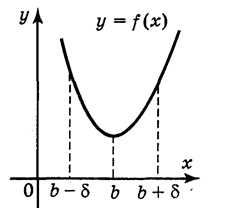
Точка  із області визначення функції
із області визначення функції 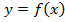 називається точкою максимуму цієї функції, якщо існує такий окіл точки
називається точкою максимуму цієї функції, якщо існує такий окіл точки  , що для всіх
, що для всіх  із цього околу виконується нерівність
із цього околу виконується нерівність
 .
.
Точка  із області визначення функції
із області визначення функції  називається точкою мінімуму цієї функції, якщо існує такий окіл точки
називається точкою мінімуму цієї функції, якщо існує такий окіл точки  , що для всіх
, що для всіх  із цього околу виконується нерівність
із цього околу виконується нерівність
 .
.
Точки максимуму і мінімуму називають точками екстремуму функції:  а значення функції цих точках називають екстремумами функції (максимум і мінімум функції):
а значення функції цих точках називають екстремумами функції (максимум і мінімум функції): 
Теорема Ферма (необхідна умова існування екстремуму функції)
Якщо функція  у внутришній точці
у внутришній точці  деякого проміжку має екстремум, то в цій точці похідна
деякого проміжку має екстремум, то в цій точці похідна 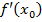 , якщо вона існує, дорівнює 0.
, якщо вона існує, дорівнює 0.
Теорема Ферма має наочний геометричний зміст: в точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт f’(хo) дорівнює нулю  .
.
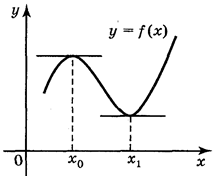
Зворотне твердження невірно: з того, що похідна дорівнює 0 в точці  не обов’язково виходить, що в цій точці функція має екстремум.
не обов’язково виходить, що в цій точці функція має екстремум.
Вибрати з критичних точок функції точки екстремуму дає можливість достатня умова.
існування екстремуму.
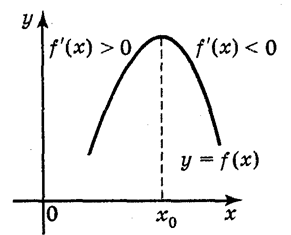
Теорема (достатня умова існування екстремуму функції)
Критична точка, при переході через яку в напрямі зростання аргументу похідна змінює знак з «плюса» на «мінус», є точкою максимуму, а точка, при переході через яку похідна змінює знак з «мінуса» на «плюс» - точка мінімуму.

Алгоритм знаходження екстремумів функції
1. Знайти 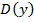 .
.
2. Знайти критичні точки функції.
3. Визначити знак похідної на проміжках, на які розбивають 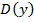 критичні точки.
критичні точки.
4. Знайти екстремальні точки: з «+» на «-«- 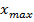 ; з «-«на «+» -
; з «-«на «+» -  .
.
5. Знайти екстремуми функції: 
22. Екстремальні точки. Дослідження функції на екстремум за допомогою другої похідної.


Точка  із області визначення функції
із області визначення функції 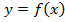 називається точкою максимуму цієї функції, якщо існує такий окіл точки
називається точкою максимуму цієї функції, якщо існує такий окіл точки  , що для всіх
, що для всіх  із цього околу виконується нерівність
із цього околу виконується нерівність
 .
.
Точка  із області визначення функції
із області визначення функції 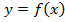 називається точкою мінімуму цієї функції, якщо існує такий окіл точки
називається точкою мінімуму цієї функції, якщо існує такий окіл точки  , що для всіх
, що для всіх  із цього околу виконується нерівність
із цього околу виконується нерівність
 .
.
Точки максимуму і мінімуму називають точками екстремуму функції:  а значення функції цих точках називають екстремумами функції (максимум і мінімум функції):
а значення функції цих точках називають екстремумами функції (максимум і мінімум функції): 
Теорема Ферма (необхідна умова існування екстремуму функції)
Якщо функція  у внутришній точці
у внутришній точці  деякого проміжку має екстремум, то в цій точці похідна
деякого проміжку має екстремум, то в цій точці похідна 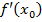 , якщо вона існує, дорівнює 0.
, якщо вона існує, дорівнює 0.
Теорема Ферма має наочний геометричний зміст: в точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт f’(хo) дорівнює нулю  .
.

Зворотне твердження невірно: з того, що похідна дорівнює 0 в точці  не обов’язково виходить, що в цій точці функція має екстремум.
не обов’язково виходить, що в цій точці функція має екстремум.
Вибрати з критичних точок функції точки екстремуму дає можливість наступне твердження:
Нехай в критичній точці  функції
функції  існує похідна другого порядку, яка не
існує похідна другого порядку, яка не
дорівнює 0: 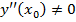 . Тоді, якщо
. Тоді, якщо  , то
, то  є точкою мінімуму, якщо
є точкою мінімуму, якщо 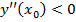 , то
, то  є точкою максимуму функції
є точкою максимуму функції 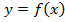 .
.
Правило дослідження функції на екстремум за допомогою другої похідної.
1. Знайти 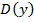 .
.
2. Знайти критичні точки функції.
3. Знайти другу похідну функції  .
.
4. Дослідити знак другої похідної в кожній критичній точці: якщо  , то
, то  - точка мінімуму, якщо
- точка мінімуму, якщо 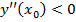 , то
, то  - точка максимуму функції. Якщо ж друга похідна дорівнює 0, то екстремум функції треба шукати за допомогою першої похідної.
- точка максимуму функції. Якщо ж друга похідна дорівнює 0, то екстремум функції треба шукати за допомогою першої похідної.
23. Знаходження найменшого і найбільшого значень функції на відрізку.
Якщо неперервна функція на заданому відрізку має скінченне число критичних точок, то вона набуває найбільшого і найменшого значення на цьому відрізку або в критичних точках, які належать цьому відрізку, або на кінцях відрізка.
Алгоритм знаходження найбільшого і найменшого значень функції на відрізку.
1. Знайти похідну функції.
2. Знайти критичні точки функції, вибрати серед них ті точки, які належать заданому проміжку.
3. Знайти значення функції в критичних точках і на кінцях проміжку.
4. Вибрати серед всіх значень найбільше і найменше.
24. Первісна. Основна властивість первісної. Невизначений інтеграл та його властивості.
Функція F(x) називається первісною функції f(x) на деякому проміжку, якщо для всіх x із цього проміжку виконується рівність: F'(x) = f(x).
Функція F(x) = sin x є первісною функції f(x) = cos x для x є R, бо (sin x)' = cos x.
Будь-яка функція  + С, де С — постійна, є первісною функції х2, оскільки (С )' =0.
+ С, де С — постійна, є первісною функції х2, оскільки (С )' =0.
Тобто для заданої функції первісна визначається неоднозначно.