sin2 α + cos2 α = l – основна тригонометрична тотожність.
З цієї формули можна виразити sin α через cos α і навпаки: 
За означенням тангенса і котангенса: 
Перемноживши ці рівності, одержимо  ·
·  = l
= l
З цієї рівності можна виразити tg α через ctg α і навпаки:

Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на соs2α ≠ 0:
 , де де
, де де 
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на sіn2 α ≠ 0:
 , де
, де 
Тригонометричні функції подвійного аргументу.
Тригонометричні функції подвійного аргументу виражають тригонометричні функції аргументу 2  через функції аргумента
через функції аргумента  .
.
Із формули  при
при  , маємо:
, маємо:

Аналогічно із формули  при
при  одержуємо:
одержуємо:

Якщо замінити за допомогою основної тригонометричної тотожності  функцію
функцію  на
на  або
або  на
на  , то матимемо ще дві формули для
, то матимемо ще дві формули для 

Із формули  при
при  , маємо:
, маємо:
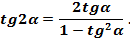
Формули зведення.
Формулами зведення називаються співвідношення, за допомогою яких значення тригонометричних функцій аргументів  , виражаються через функції кута α.
, виражаються через функції кута α.
Для того щоб записати будь-яку з них, можна користуватися таким правилом:
1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < α <  .
.
2) Якщо в лівій частині формули кут дорівнює  ± α,
± α,  ± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується.
± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується.
Наприклад:  ;
; 
За допомогою формул зведення знаходження значень тригонометричних функцій будь-якого кута можна звести до знаходження тригонометричних функцій гострого кута.

Тригонометричні рівняння. Розв’язування рівняння.
Рівняння, які містять змінну лише під знаком тригонометричної функції, називаються тригонометричними рівняннями.
Арксинусом числа  називається таке число (кут) із проміжку
називається таке число (кут) із проміжку  , синус якого дорівнює
, синус якого дорівнює  .
.

Рівняння.

Якщо  , то рівняння
, то рівняння  не має розв´язків, оскільки
не має розв´язків, оскільки  для будь – якого
для будь – якого 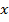 .
.
Якщо  , то враховуючи те, що синус – це ордината точки одиничного кола, маємо: ординату, рівну
, то враховуючи те, що синус – це ордината точки одиничного кола, маємо: ординату, рівну  , мають дві точки одиничного кола:
, мають дві точки одиничного кола:

Враховуючиперіодичність  , маємо:
, маємо:

Ці дві формули можна записати у вигляді однієї формули:

При парному  маємо
маємо  , при непарному
, при непарному 
 .
.

Тригонометричні рівняння. Розв’язування рівняння.
Рівняння, які містять змінну лише під знаком тригонометричної функції, називаються тригонометричними рівняннями.
Арккосинусом числа  називається таке число (кут) із проміжку
називається таке число (кут) із проміжку  , косинус якого дорівнює
, косинус якого дорівнює  .
.

Рівняння.

Якщо  , то рівняння
, то рівняння  не має розв´язків, оскільки
не має розв´язків, оскільки  для будь – якого
для будь – якого 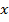 .
.
Якщо  , то враховуючи те, що косинус – це абсциса точки одиничного кола, маємо: абсцису, рівну
, то враховуючи те, що косинус – це абсциса точки одиничного кола, маємо: абсцису, рівну  , мають дві точки одиничного кола:
, мають дві точки одиничного кола: 
Враховуючиперіодичність  , дістанемо множину розв´язків рівняння
, дістанемо множину розв´язків рівняння  :
:








