Числова функція. Основні властивості функції та її графік

Числовою функцією з областю визначення називають таку залежність, при якій кожному числу 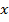з множини відповідає одне дійсне число : .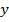

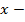незалежна змінна або аргумент, 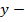залежна змінна або функція.

Множину всіх значень незалежної змінної 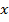називають областю визначення функції . Множину значень функції, яких вона набуває при всіх значеннях 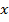з її області визначення, називають множиною значень функції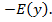

Основними способами задання функції є аналітичний (за допомогою формули), графічний і табличний.

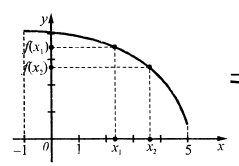
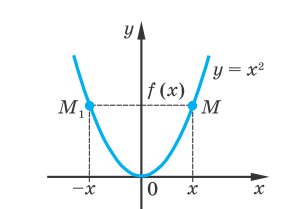
Функція називається зростаючою (спадною) на проміжку, якщо більшому значенню аргументу з цього проміжку відповідає більше (менше) значення функції.

 

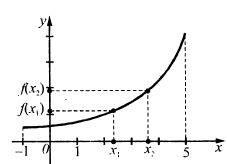
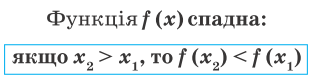
2. Функція , її графік і властивості.

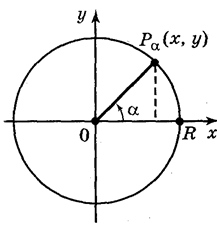
Синусом числа 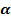називається ордината точки 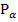одиничного кола, в яку переходить початкова точка 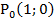при повороті навколо центра кола на кут радіан - .

Крива, яка є графіком функції у = sin x, називається синусої­дою.

Властивості функції :

1. Область визначення функції – множина всіх дійсних чисел: .
2. Множина значень функції – проміжок : .
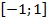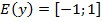3. Непарна функція: .

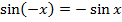Графік функції симетричний відносно початку координат.

1. Періодична функція з найменшим додатним періодом : .
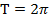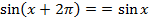2. Точки перетину з осями координат:

з віссю О 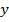: 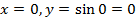, тобто графік проходить через (0;0) – початок координат;

з віссю О : .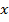

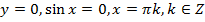1. Проміжки знакосталості:

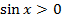, якщо 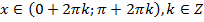– І і ІІ чверті на одиничному колі;

, якщо 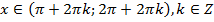– ІІІ і І 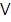чверті на одиничному колі.

1. Проміжки монотонності:

функція зростає на кожному з проміжків

і спадає на кожному з проміжків .

1. Найменші значення функції: 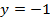, якщо .
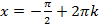2. Найбільші значення функції: 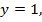якщо .

 

 

3. Функція , її графік і властивості.

Косинусом числа 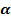називається абсциса точки 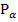одиничного кола, в яку переходить початкова точка 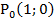при повороті навколо центра кола на кут радіан - .

 

 

Графіком функції є косинусоїда.

Властивості функції :

1. Область визначення функції – множина всіх дійсних чисел: .
2. Множина значень функції – проміжок : .
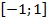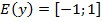3. Парна функція: 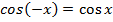. Графік функції симетричний відносно осі О .
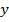4. Періодична функція з найменшим додатним періодом : .
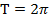5. Точки перетину з осями координат:

з віссю О 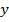: 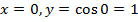; з віссю О : .

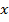1. Проміжки знакосталості:

, якщо – І і І 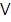чверті на одиничному колі;

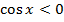, якщо – ІІ і III чверті на одиничному колі.

1. Проміжки монотонності:

функція зростає на кожному з проміжків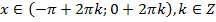

і спадає на кожному з проміжків .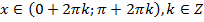

1. Найменші значення функції: 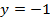, якщо .
2. Найбільші значення функції: 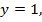якщо .

 

 

4. Функція , її графік і властивості.

Тангенсом числа 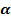називається відношення : .

 

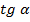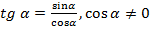Графіком функції є тангенсоїда.

Властивості функції :

1. Область визначення функції –

2. Множина значень функції – .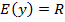

3. Непарна функція: .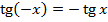

Графік функції симетричний відносно початку координат.

4. Періодична функція з найменшим додатним періодом : .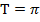

5. Точки перетину з осями координат:

з віссю О 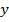: 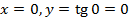, тобто графік проходить через початок координат;

з віссю О : .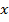

6. Проміжки знакосталості:

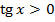, якщо – І і ІІI чверті на одиничному колі;

, якщо – ІІ і І 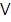чверті на одиничному колі.

7. Проміжки монотонності:

функція зростає на кожному з проміжків .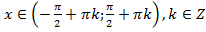

8. Найменших значень функція немає.

9. Найбільших значень функція немає.