Теорема об эквивалентном источнике напряжения. (Теорема Таневена)

Ток в любой ЛЭЦ не изменяется, если электрическая цепь к которой подключена данная ветвь заменить эквивалентным источником напряжения, ЭДС которого равна напряжению на зажимах разомкнутой цепи, а внутреннее сопротивление источника равно входному сопротивлению пассивной электрической цепи со стороны зажимов разомкнутой ветви.

 

ЛЭЦ i R

 

R_BH

 

U_XX i R

 

Метод холостого хода.

1. Находим напряжение на зажимах разомкнутой ветви (U_хх).

2. Определяем входное сопротивление всей схемы относительно разомкнутых зажимах при замкнутой внутренней ЭДС.

3. Вычисляем искомый ток по формуле.

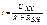
R₁ a R₂

 

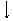E₁ R₃ i₃ E₂

 

 

б

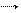i R₁ a R₂

 

 

E₁ U_XX E₂

 

 

б

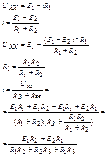
Теорема об эквивалентом источнике тока. (Теорема Нортона).

Ток в любой ветви линейной электрической цепи не изменяется, если электрическая цепь, к которой подключена данная ветвь заменить экв. ист. тока, ток кокорой равен тока протекающему между зажимами ветви замкнутыми накоротко, а внутренняя проводимость источника равна входной проводимости пассивной электрической цепи со стороны зажимов при разомкнутой ветви.

R_BH

 

U_XX R

 

 

 

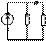E₁ R_BH R

 

 

R₁ R₂

a

R_BH

б

 

 

Метод короткого замыкания предполагает следующие действия:

1. Определение тока КЗ, путем замыкания контактов.

2. Определение внутреннего сопротивления или проводимости при разомкнутой цепи и исключенных источниках тока.

3. Расчет тока через интересующую вевть по ф-ле:

 

 

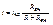
Гармонические колебания.

i(t)=I(t+T)

T – период периодической ф-ии.

f=1/T [Гц]=1/c

i(t)=I_m*sin(wt+j)

I_m – амплитуда

w – угловая частота

w=2pf=2p/T [рад/с]

j - начальная фаза

wt – угол

 

Среднее действующее значение действующего тока.

f(t)=f(t+T)

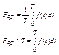
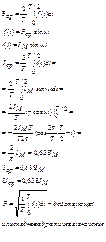
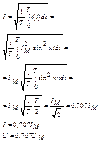
Действующее значение периодического тока равно по величине постоянному току, который проходя через постоянное сопротивление R за период времени Т выделяет то же количество тепла, что и данный периодический ток.

 

Гармонический ток в сопротивлении.

i(t) R

 

U(t)

U(t)=Umcos(wt+j_m)

i(t)=U(t)/R=(Um/R)*cos (wt+j_u)

i(t)=Im*cos(wt+j_I); Im=Um/R;

j_I=j_u; y=j_u-j_I=0

Im

Um

j_u j_I

 

 

P_R(t)=U(t)*I(t)=Um*Im*cos²(wt+j_U=

Um*Im*(1+cos2(wt+j_U))/2=

UI(1+cos2(wt+j_U));

PÎ[0;2U]

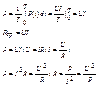
R – Активное сопротивление при переменном токе.

13. Гармонический ток в индуктивности.

 

L

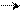
i(t)

U(t)

 

i(t)=Im*cos (wt+j_I)

e_L= - Ldi(t)/dt=-Limw(-sin(wt+j_I))

e_L(t)= - U_L(t)

U_L(t)= - Limwsin(wt+j_I)=ImwL*

*cos(wt+j_I+p/2)

U_L(t)=Um* cos(wt+j_u),

где j_u=j_I+p/2

X_l=wL

Um=ImX_L

Um Im

j_u=j_I+p/2

 

p/2

j_I

 

P_L(t)=U(t)*i(t)= - ImUmcos(wt+j_I)*

sin(wt+j_I)= - (ImUm*sin2(wt+j_I))/2

P_L(t)= IU*sin2(wt+j_I)