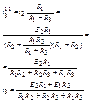Перенос источников напряжения в схемах

Идеальные источники тока и напряжения.

Источник напряжения – активный элемент с двумя зажимами, напряжение на котором не зависит от тока проходящего через истоочник

 

 

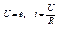
Источник ЭДС

i

i=var

 

Источник тока

 

е U R

Если R=0 то и а это невозможно
Схема реального источника напряжения:

r

 

 

i

Идеальный источник тока – активный элемент, ток которого на зависит от напряжения на его выводах.

 

 

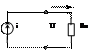
Стрелка указывает положительное напряжение тока i(t) или полярность источника

i1

Схема реалбного источника тока:

 

 

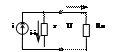
i=const;

при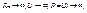

Поэтому идеальный источн. тока так же как и источн. напряжения рассматривается как источник бесконечной мощности.

Реальный иточн. – источн. конечной мощности.

 

Законы Киргофа.

1-й) Алгебраическая сума токов входящих в узел равна 0:

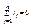
2-й) Алгебраическая сумма ЭДС в любом контуре в цепи равна алгебраической сумме падений напряжений на элементах этого контура.

Последовательные, паралельные и смешанные соединения.

R1 R2 Rn

Последовательное соединение:

 

 

Паралельное соединение:

 

i

i1 i2 in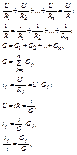

 

 

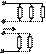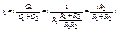
i=i₁=i₂+…i_n=

R1 R2

 

R1 R2 R3

 

i

 

i2

i1

R1 R2

 

 

ток в паралельной ветви равен произведению тока в неразветвлённой части на дробь, в числителе которой сопротивление противоположной ветви, а в знаменателе сумма сопротивлений паралельных ветвей.

 

Смешанное соединение:

 

R2 R3

 

 

 

4. Перобразование соединения типа “треугольник” в эквивалентную “звезду”.

 

Преобразования наз. эквивалентными, если внешние токи и напряжения неизменны.

“Треугольник”:

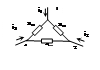“Звезда”:

 

 

(2-й закон Киргофа)

i1

Условие эквивалентности:

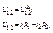
эквивалентность выполняется если:

i

Сопротивление в лучах эквивалентной “звезды” равно произведению сопротивлений прилегающих сторон треуголиника

делёному на сумму сопротивлений 3-х сторон треугольника.

 

Преобразование соединения типа “ звезда ” в эквивалентный “треугольник ”.

 

“Треугольник”:

 

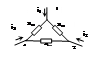
“Звезда”:

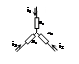Сопротивление стороны эквивалентного треугольника равно сумме сопротивлений прилегающих лучей звезды плюс их произведение делённое на сопротивление третьего луча.

 

i1

5. Эквивалентные источники напряжения и тока

 

 

i1

i

 

 

 

i-i1

 

 

(условие эквивалентности)

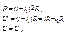
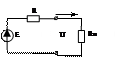
Источник напряжения (рис. 1) можна заменить на эквивалентный источник тока (рис. 2) (см. условие эквивалентности)

in+1

6. Преобразование схем с двумя узлами.

 

i2

i1

 

 

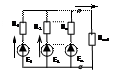
заменим все источники напряжения на источники тока.

Rn+1

 

 

in+1

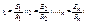
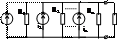
эта схема будет эквивалентна следующей:

 

 

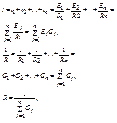
заменив источник тока на источник напряжения мы упростили первоначальную схему до такой:

 

 

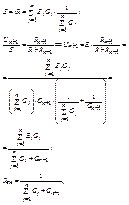
Перенос источников напряжения в схемах.

Источник ЕДС может быть перенесён из какой либо ветви схемы во все остальные ветви присоеденённые к узлу данной ветви, без изменения токов в схеме.

Справедливо и обратное.

 

 

 

↓

 

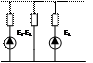
Если во всех ветвях цепи, кроме одной, имеются одинаковые ЕДС направленные к одному узлу или то узла, то они могут быть заменены одним источникомЕДС в находящейся ветви, в которой она отсутствовала.

 

↓

 

Источник тока может быть заменён несколькими источниками тока, подключёнными параллельно всем ветвям которые составляли контур с рассматриваемым источником.

 

 

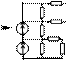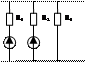
8. Метод контурных токов.

Задаём контурный ток. Направление токов должно быть либо ¿, либо в другом направлении, но они должны быть одинаковыми.

R₁ R₂

i₁ i₂

E₁ R₃ E₂

 

 

 

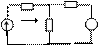
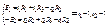
i₁

i₂

9. Метод наложения или метод суперпозиции.

Правило для схем с источниками напряжения.

Ток в любом контуре линейной электрической цепи может быть получен как алгебраическая сумма токов вызываемых в этом контуре каждой из ЭДС в отдельности.

Правило для схем с источниками токов.

Узловое напряжение любого узла линейной электрической цепи может быть получено как алгебраическая сумма напряжений вызываемых в этом узле каждым из задающих токов в отдельности.

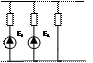
R₁ R₂

i₁

E₁ R₃ E₂

 

Найти і₃ -?.

i₃=i₃¹+i₃¹¹

R₁ R₂

i₁

E₁ R₃

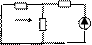R₁ R₂

i₁

R₃ E₂