ОРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛООТДАЧИ
МЕТОДОМ РЕГУЛЯРНОГО РЕЖИМА
Назначение.
Установка предназначена экспериментального определения коэффициента теплоотдачи при медленном нагревании (охлаждении) металлических цилиндрических образцов в воздушном термостате.
Теоретические основы работы.
Связь между временными и пространственными изменениями температуры в любой точке тела, в которых происходит процесс теплопроводности устанавливается уравнением теплопроводности. Для тела, в котором отсутствуют источники тепла, оно принимает вид: 
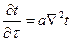, (1)
где a – коэффициент температуропроводности, м2/с. Он является физическим параметром вещества и является мерой теплоинерционных свойств тела. При прочих равных условиях выравнивание температур во всех точках тела будет происходить быстрее, чем больше коэффициент температуропроводности.
, (2)
где l - коэффициент теплопроводности; с – удельная теплоёмкость вещества; r - плотность вещества.
Решение уравнения (1) производится с помощью рядов Фурье. Для различных краевых условий результаты получаются различными, но методология решения, в основном, одинакова. Искомая функция уравнения (1) зависит от большого числа переменных, но при более глубоком анализе решений оказывается, что эти переменные можно сгруппировать в три безразмерных комплекса. Эти комплексы являются критериями подобия:
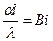- критерий Био,
- критерий Фурье,
- критерий геометрического подобия.
При изменении температуры среды, в которой нагревается тело по линейному закону и при постоянном тепловом потоке поглощаемым телом имеет место условия
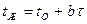и a = const. (3)
При этом температура в любой точке тела является линейной функцией времени, а распределение температур – параболой. Этот режим нагревания носит название регулярного режима второго рода или квазистационарного теплового режима.
При малых Bi температура на поверхности тела незначительно отличается от температуры на его оси. Это возможно для металлов, у которых величина температуропроводности достаточно велика (медь, дюраль). В этом случае нагрев или охлаждение тела определяется интенсивностью теплоотдачи на его поверхности, а процесс выравнивания температуры в теле происходит существенно быстрее, чем подвод или отвод теплоты с поверхности тела.
Решение задачи о нагревании (охлаждении) тел приводит к понятию темпа нагрева (охлаждения):
(4)
Левая часть определяет относительную скорость изменения температуры, которая при регулярном режиме не зависит от координат и времени и является постоянной величиной. Можно показать, что
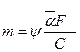(5)
Формула (5) отражает содержание первой теоремы Кондратьева:
Темп охлаждения (нагревания) однородного и изотропного тела при конечном значении коэффициента теплоотдачи пропорционален коэффициенту теплоотдачи, площади поверхности тела и обратно пропорционален его теплоёмкости.
Множитель y называется коэффициентом неравномерности распределения температуры. В случае медленного нагрева металлических образцов y=1.
А.В. Лыковым было показано регулярный режим определяется не только определёнными температурными полями, возникающими в нагреваемом или охлаждаемом теле, но и потоками тепла через его поверхность. Поэтому при нагревании металлических образцов нет необходимости различать регулярные режимы первого, второго и третьего рода. В качестве общего свойства теплового регулярного режима можно принять соотношение
, (6)
где 
-средняя по объёму температура тела; 
- температура среды.
Из соотношений (5) и (6) следует
(7)
где, Суд – удельная теплоемкость исследуемого образца, а М – масса образца.
