144.Обобщенный гармонический ряд 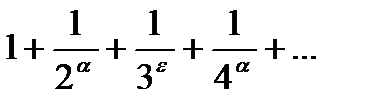 расходится при каких значениях
расходится при каких значениях 
 -ның қандай мґнiнде
-ның қандай мґнiнде 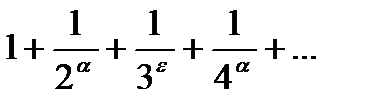 гармоникалық қатары жинақталады
гармоникалық қатары жинақталады





145.Геометрический ряд a+aq+aq2+aq3+…, a  0 расходится, если
0 расходится, если
a+aq+aq2+aq3+…, a  0 геометриялық қатары жинақталады, егер
0 геометриялық қатары жинақталады, егер


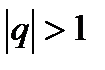


146.С помощью какого признака доказывается, сходится или расходится обобщенный гармонический ряд
қандай белгiге байланысты гармоникалық қатардыє жинақталуы не жинақталмауы дәлелденедi
интегрального признака
интегралдық белгiге
признака Даламбера
Даламбер белгiсiне
признака Коши
Коши белгiсiне
признака Лейбница
Лейбниц белгiсiне
необходимого признака
қажеттiлiк белгiсiне
147.Сходимость числового ряда  по признаку Даламбера: ряд сходится, если
по признаку Даламбера: ряд сходится, если
 сандық қатары Даламбер белгiсi бойынша жинақталады, егер
сандық қатары Даламбер белгiсi бойынша жинақталады, егер





148.Сходимость числового ряда  по признаку Коши: ряд сходится, если
по признаку Коши: ряд сходится, если
 сандық қатары Коши белгiсi бойынша жинақталады, егер
сандық қатары Коши белгiсi бойынша жинақталады, егер





149.Предельный признак сравнения: если  и
и  ряды с положительными членами и существует …, то ряды одновременно сходятся или расходятся
ряды с положительными членами и существует …, то ряды одновременно сходятся или расходятся
Шектiк салыстыру белгiсi егер  жґне
жґне  қатарлары оң мүшелi болып жґне … орындалса, онда қатарлар бiр уақытта жинақталады не жинақталмайды
қатарлары оң мүшелi болып жґне … орындалса, онда қатарлар бiр уақытта жинақталады не жинақталмайды





150.По признаку Даламбера: ряд  расходится, если
расходится, если
 сандық қатары Даламбер белгiсi бойынша жинақталмайды, егер
сандық қатары Даламбер белгiсi бойынша жинақталмайды, егер
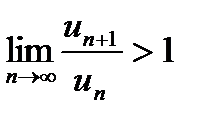




151.По признаку Коши: ряд  расходится, если
расходится, если
 сандық қатары Коши белгiсi бойынша жинақталмайды, егер
сандық қатары Коши белгiсi бойынша жинақталмайды, егер





152.Интегральный признак сходимости: для сходимости положительного и не возрастающего члена an=f(n) числового ряда необходимо и достаточно чтобы сходился несобственный интеграл …
Жинақталудыє интегалдық белгiсi оң мүшелi өспейтiн an=f(n) сандық қатары жинақталуы үшiн оның … меншiксiз интегралы жинақталуы қажеттi жґне жеткiлiктi





153.Какой признак используется для исследования сходимости знакочередующегося ряда
Айнымалы таңбалы қатарыныє жинақталуы қандай белгi арқылы зерттеледi
признак Лейбница
Лейбниц белгiсi
признак Даламбера
Даламбер белгiсi
признак Коши
Коши белгiсi
интегральный признак
интегралдық белгi
необходимый признак
қажеттi белгi
154.Какие условия (условие) проверяются при исследовании сходимости знакочередующегося ряда
Айнымалы таңбалы қатарлардың жинақталуын зерттеуде қандай шарттар тексерiледi





155) Чья эта формула: 
Формуланың аталуы
a) Байеса
b) Бернулли
c) Пуассона
d) Лагранжа
e) Лапласа
156) Укажите формулу полной вероятности:
Толық ықтималдылықтың формуласын көрсет.
a) Р(А)= 
b) Р(А)=Р(А 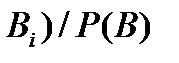
c) Р(А)=Р(В) 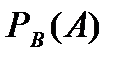
d) Р(А+В+С)=Р(А)+ 
e) Р(А)+Р(В)=1
157) Чему равна сумма вероятностей событий, образующих полную группу?
Толық топты құрайтын оқиғалардың ықтималдықтарының қосындысы неге тең?
a) 1
b) 0
c) 0<p<1
d) p<0
e) 
158) Функцией распределения называется
Жiктеу функциясы дегенiмiз
a) F(x)=P(X<x)
b) F(x)=P(x)
c) f(x)=P(X<x)
d) F(x)=P(X)
e) f(x)=P(X, x)
159) Плотностью распределения вероятностей непрерывной СВ Х называется
Үзiлiссiз кездейсоқ Х шаманың тығыздықтық жiктеу ықтималдылығы дегенiмiз
a) f(x)=F’(x)
b) F(x)=f ’(x)
c) f(X)=F’(x)
d) F(x)=f ’(x)
e) f(X)=F’(x)
160) Найти функцию распределения, выраженную через плотность распределения
Тығыздық жiктеу арқылы берiлген жiктеу функциясын табу
a) F(x)= 
b) F(x)= 
c) f(x)= 
d) F(x)= 
e) f(x)= 
161) Функция распределения F(x) всегда:
F(x) функциясының жiктеуi үнемi:
a) 0 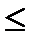 F(x)
F(x) 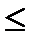 1
1
b) 0 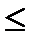 F(x)
F(x)
c) 0  F(x)
F(x)  1
1
d) 0.5 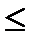 F(x)
F(x) 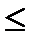 1
1
e) 0 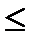 F(x)
F(x) 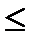 2
2
162) Математическое ожидание для непрерывной случайной величины:
Үздiксiз кездейсоқ шамаға арналған математикалық күтiм:
a) М(Х)= 
b) М(Х)= 
c) М(Х)= 
d) М(Х)= 
e) М(Х)= 
163) Математическое ожидание для дискретной случайной величины:
Кездейсоқ дискреттi шама үшiн математикалық күтiм:
a) М(Х)= 
b) M(X)= 
c) M(X)= 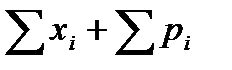
d) M(X)=  )
)
e) M(X)= 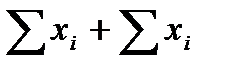
164) Математическое ожидание отклонения равно:
Математикалық күтiмнiң ауытқуы тең:
a) М[X-M(x)]=0
b) M[X-M(X)]=1
c) M[M(X)-X]=0
d) M[y-M(X)]=0
e) M[M(x)-y]=1
165) Выберете формулу дисперсии дискретной СВ:
Кездейсоқ дискретiк шаманың дисперсиясының формуласын таңда:
a) D(X)= 
b) D(X)= 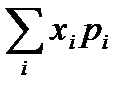
c) D(X)= 
d) D(X)=M(X) 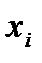
e) D(X)= 
166) Выберете формулу дисперсии непрерывной СВ:
Үздiксiз кездейсоқ шаманың дисперсиясының формуласы:
a) D(X)= 
b) D(X)= 
c) D(X)= 
d) D(X)= 
e) D(X)= 
167) Среднеквадратичное отклонение:
Орташа квадраттық ауытқу:
a) s(x)= 
b) s(x)= 
c) s(x)= 
d) s(x)= 
e) s(x)= 
168.Дифференциальное уравнение с разделенными переменными имеет вид
Айнымалылары бөлiнген дифференциял теңдеудiң түрi.
M(x)dx+N(y)dy=0
M1(x)N1(y)dx+M2(x)N2(y)dy=0



169.Дифференциальное уравнение с разделяющимися переменными имеет вид
Айнымалылары бөлiнетiн дифференциял теңдеудiң түрi.
a) M1(x)N1(y)dx+M2(x)N2(y)dy=0
b) M(x)dx+N(y)dy=0
c) 
d) 
e) 
170.Линейное дифференциальное уравнение первого порядка имеет вид
Бiрiншi реттi сызықты дифференциял теңдеудiң түрi.

M1(x)N1(y)dx+M2(x)N2(y)dy=0
M(x)dx+N(y)dy=0


171.Уравнение Бернулли имеет вид
Бернулли теңдеуiнiң түрi
a) 
b) 
c) M1(x)N1(y)dx+M2(x)N2(y)dy=0
d) M(x)dx+N(y)dy=0
e) 
172.Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
Екiншi реттi тұрақты коэффициенттi дифференциял теңдеудiң түрi.



M1(x)N1(y)dx+M2(x)N2(y)dy=0
M(x)dx+N(y)dy=0
173.Дифференциальное уравнение 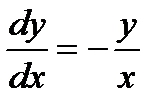 является
является
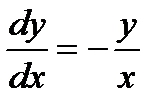 Дифференциялдық теңдеу болады
Дифференциялдық теңдеу болады
a) Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн теңдеу
b) Уравнением с разделенными переменными
Айнымалылары бјлiнген теєдеу
c) Уравнением Бернулли
Бернулли теңдеуi
d) Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теєдеу
e) Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
174.Екiншi реттi сызықты тұрақты коэффициеттi дифференциял теңдеу.
Дифференциальное уравнение  является
является
 Дифференциял теєдеу болады
Дифференциял теєдеу болады
Линейным уравнением первого порядка
Бiрiншi реттi сызықты дифференциял теңдеу
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi дифференциял теєдеу
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн дифференциял теңдеу
Уравнением с разделенными переменными
Айнымалылары бөлiнген дифференциял теңдеу
Уравнением Бернулли
Бернулли теңдеуi
175.Дифференциальное уравнение  является
является
 Дифференциял теңдеу болады
Дифференциял теңдеу болады
Уравнением с разделенными переменными
Айнымалылары бөлiнген дифференциял теңдеу
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн дифференциял теңдеу
Уравнением Бернулли
Бернулли теңдеуi
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теєдеу
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
176). Указать верную формулу относительной частоты события:
Оқиғаның салыстырмалы жиiлiктiң формуласын көрсет:
a) w(A)=m/n
b) w(A)=m!/n
c) w(A)=(m+n)/n
d) w(A)=1/n
e) w(A)=mn
177. Тұрақты коэффициенттi екiншi реттi сызықты бiртектi дифференциял теңдеу
Дифференциальное уравнение ydx-xdy=0 является
ydx-xdy=0 Дифференциял теңдеу болады
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн дифференциял теңдеу
Уравнением с разделенными переменными
Айнымалылары бөлiнген дифференциял теңдеу
Уравнением Бернулли
Бернулли теңдеуi
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теєдеу
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
178. Тұрақты коэффициенттi екiншi реттi сызықты бiртектi дифференциял теңдеу
Дифференциальное уравнение  является
является
 Дифференциял теєдеу болады
Дифференциял теєдеу болады
Линейным уравнением первого порядка
Бiрiншi реттi бiртектi сызықты теңдеу
Уравнением с разделенными переменными
Айнымалылары бјлiнген дифференциял теєдеу
Уравнением Бернулли
Бернулли теңдеуi
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теєдеу
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
179. Тұрақты коэффициенттi екiншi реттi сызықты бiртектi дифференциял теңдеу
Дифференциальное уравнение  является
является
 Дифференциял теєдеуболады
Дифференциял теєдеуболады
Уравнением Бернулли
Бернулли теңдеуi
Линейным уравнением первого порядка
Бiрiншi реттi сызықты теңдеу
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теңдеу
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн теңдеу
Уравнением с разделенными переменными
Айнымалылары бөлiнген теңдеу
180.Для дифференциального уравнения  характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
 дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
a) 
b) 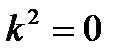
c) 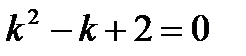
d) 
e) 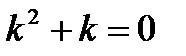
181.Для дифференциального уравнения  характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
 дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi

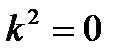


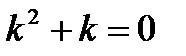
182.Для дифференциального уравнения  характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
 дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
a) 
b) 
c) 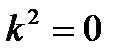
d) 
e) 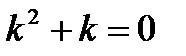
183.Для дифференциального уравнения  характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
 дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi

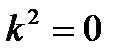



184.Корнями характеристического уравнения дифференциального уравнения  будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
a) 
b) 
c) 
d) 
e) 
185.Корнями характеристического уравнения дифференциального уравнения  будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны





186.Корнями характеристического уравнения дифференциального уравнения  будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
a) 
b) 
c) 
d) 
e) 
187.Корнями характеристического уравнения дифференциального уравнения  будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны






