Бiртектi
E) Определенной
Анықталған
30.Система уравнений, у которой существует единственное решение, называется
Теңдеулер жүйесiнiң жалғыз шешiмi болса,қалай аталады
A) Определенной
Анықталған
B) Единичной
Бiрлiк
C) Нулевой
Нөлдiк
D) Неоднородной
Бiртектiемес
E) Однородной
Бiртектi
31.Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если
n айнымалысы бар m теңдеуден тұратын теңдеулер жүйесi бiртектi деп аталады, егер
A) Все их свободные члены равны нулю
Оң жағындағы бос мүшенiң барлығы нольге тең
B) Их свободные члены не равны нулю
Бос мүшесiнiң бiреуi нольге тең
C) Система имеет хотя бы одно решение
Теңдеудiн ең болмағанда бiр шешiмi бар
D) Система имеет множество решений
Шешiмi көп
E) Система не имеет решений
Шешiмi жоқ
32.Система m линейных уравнений с n переменными называется системой линейных неоднородных уравнений, если
n айнымалысы бар m теңдеуден тұратын теңдеулер жүйесi бiртектi емес, егер
A) Хотя бы один из свободных членов не равен нулю
Оң жағындағы бос мүшенiң ең болмағанда бiреуi ноль емес
B)Система имеет хотя бы одно решение
Бәрi ноль емес
C)Система имеет множество решений
Бәрi нольге тең
D) Все их свободные члены равны нулю
Бос мүшесiнiң жартысы нольге тең
E) Система не имеет решений
Шешiмi жоқ
33.Если в системе уравнений
Егер теңдеулер жүйесi мына түрде берiлсе,қалай аталады
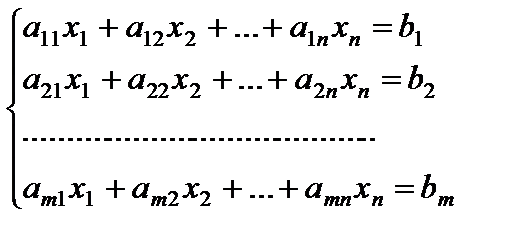 b1 =b2 =…=bm=0, то система называется
b1 =b2 =…=bm=0, то система называется
A) Однородной
Бiртектi
B) Неоднородной
Бiртектiемес
C) Несовместной
Үйлесiмсiз
D) Нулевой
Нөлдiк
E) Определенной
Анықталған
34.В матрице А= 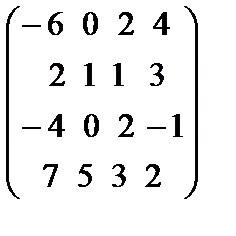 побочную диагональ составляют элементы
побочную диагональ составляют элементы
А= 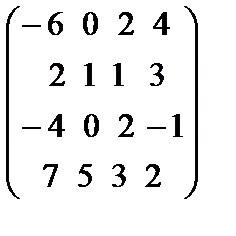 Матрицасының көмекшi диогоналының элементтерiн жаз
Матрицасының көмекшi диогоналының элементтерiн жаз
A) 4,1,0,7
B) 7,5,3,2
C) –4,0,2,-1
D) –6,1,2,2
E) –6,1,-2,-2
35.В матрице А=  главную диагональ составляют элементы
главную диагональ составляют элементы
А=  Басты диогоналының элементтерiн жаз
Басты диогоналының элементтерiн жаз
A) –6,1,7,3
B)2,1,6,0
C)–6,4,-3,0
D) 2,3,8,3
E) 0,1,6,0
36.В матрице А= 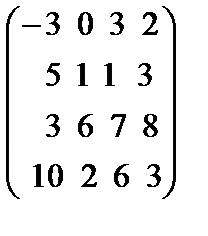 побочную диагональ составляют элементы
побочную диагональ составляют элементы
А=  Матрицасының көмекшi диогоналының элементтерiн жаз
Матрицасының көмекшi диогоналының элементтерiн жаз
A) 2,1,6,10
B) –3,1,7,3
C) –3,5,3,10
D) 2,3,8,3,
E) 10,2,6,3
37.В матрице А=  главную диагональ составляют элементы
главную диагональ составляют элементы
А=  Басты диогоналының элементтерiн жаз
Басты диогоналының элементтерiн жаз
A) –3,1,7,3
B)–3,5,3,10
C)2,3,8,3,
D) 10,2,6,3
E) 2,1,6,10
38.Найти алгебраическое дополнение А11 матрицы 
Матрицаның А11 алгебралық толықтауышын есепте
A) 30
B) –30
C) 8
D) –8
E) 2
39.Найти алгебраическое дополнение А12 матрицы 
Матрицаның А12 алгебралық толықтауышын есепте
A) -12
B) 4
C) 12
D) 8
E) 30
40.Найти алгебраическое дополнение А13 матрицы 
Матрицаның А13алгебралық толықтауышын есепте
A) 6
B) 13
C) –7
D) 14
E) -6
41.Найти алгебраическое дополнение А21 матрицы 
Матрицаның А21 алгебралық толықтауышын есепте
A) –2
B) 2
C) 6
D) –6
E) 5
42.Найти алгебраическое дополнение А22 матрицы 
Матрицаның А22 алгебралық толықтауышын есепте
A) 8
B) –8
C) –2
D) 2
E) 6
43.Найти алгебраическое дополнение А23 матрицы 
Матрицаның А23 алгебралық толықтауышын есепте
A) –4
B) 4
C) –2
D) –11
E) 6
44.Найти алгебраическое дополнение А31 матрицы 
Матрицаның А31 алгебралық толықтауышын есепте
A) –23
B) 23
C) 6
D) –6
E) 28
45.Найти алгебраическое дополнение А32 матрицы 
Матрицаның А32 алгебралық толықтауышын есепте
A) 11
B) –11
C) 16
D) 6
E) -6
46.Найти алгебраическое дополнение А33 матрицы 
Матрицаның А33 алгебралық толықтауышын есепте
A) 8
B) –8
C) 6
D) –6
E) 20
47.Найти минор М11 матрицы 
Матрицаның М11 минорын тап
A) 30
B)–30
C)8
D) –8
E) 2
48.Найти минор М12 матрицы 
Матрицаның М12 минорын тап
A) 12
B) 4
C) -12
D) 8
E) 30
49.Найти минор М13 матрицы 
Матрицаның М13минорын тап
A) 6
B) 13
C) –7
D) 14
E) -6
50.Найти минор М21 матрицы 
Матрицаның М21 минорын тап
A) 2
B) -2
C) 6
D) –6
E) 5
51.Найти минор М22 матрицы 
Матрицаның М22 минорын тап
A) 8
B) –8
C) –2
D) 2
E) 6
52.Найти минор М23 матрицы 
Матрицаның М23 минорын тап
A) 4
B) -4
C) –2
D) –11
E) 6
53.Найти минор М31 матрицы 
Матрицаның М31минорын тап
A) –23
B) 23
C) 6
D) –6
E) 28
54.Найти минор М32 матрицы 
Матрицаның М32 минорын тап
A) -11
B) 11
C) 16
D) 6
E) -6
55.Найти минор М33 матрицы 
Матрицаның М33 минорын тап
A) 8
B) –8
C) 6
D) –6
E) 20
56.При умножении всех элементов некоторой строки матрицы на число определитель исходной матрицы
Матрицаның кез-келген қатарыныє элементтерiн санға көбейтсек матрица анықтауышы
A) Умножается на это число
Осы санға көбейтiледi
B) Увеличивается на это число
Осы санға үлкейедi
C) Не меняется
Їзгермейдi
D) Меняет знак
Таңбасы өзгередi
E) Нет правильного ответа
Дѕрыс жауабы жоқ
57.Если две строки матрицы равны, то ее определитель
Матрицаныє екi қатары нөлге тең болса,онда анықтауыш неге тең
A) det =0
B) det  0
0
C) det >0
D) det <0
E) det =1
58.Если какая-либо строка (столбец) матрицы состоит из одних нулей,
то ее определитель
Егер матрицаныє қандайда бiр қатары жґне тiк жолы нөлден тұратын болса,матрицаның анаықтауышы
A) det =0
B) det  0
0
C) det >0
D) det <0
E) det =1
59.При транспонировании матрицы ее определитель
Тронспонирленген матрицаның анықтауышы
A) Не изменяется
Өзгермейдi
B) Меняет знак на противоположный
Таңбасы керi таңбаға ауысады
C) Увеличивается на 1
1-санµа ѕлкейедi
D) Уменьшается на 1
1-санға азайады
E) Превращается в 0
Нөлге айналады
60.При перестановке двух строк (столбцов) матрицы ее определитель
Матрицаның қатарын және тiк жолын ауыстырғанда матрицаның анықтауышы
A) Меняет знак на противоположный
Таңбасы керi таєбаға ауысады
B) Не изменяется
Өзгермейдi
C) Увеличивается на 1
1-санға үлкейедi
D) Уменьшается на 1
1-санға азайады
E) Превращается в 0
Нөлге айналады
61.Если квадратная матрица содержит две одинаковые строки (столбца),
то ее определитель
Егер квадратты матрица екi бiрдей қатардан жґне тiкжолдан тұрса,онда матрицаның анықтауышы
A) det =0
B) det  0
0
C) det >0
D) det <0
E) det =1
62.Если элементы двух строк (столбцов) матрицы пропорциональны, то
ее определитель
Егер матрицаның екi қатары жґне тiк жолы пропорциональ болса,онда анықтауышы
A) det =0
B) det  0
0
C) det >0
D) det <0
E) det =1
63.Размер матрицы С=А1х2×В2х3 равен
С=А1х2×В2х3 Матрицаның өлшемi неге тең
A) С1х3
B) С2х2
C) С1х2
D) С2х3
E) С2х6
64.Размер матрицы С=А2х2×В2х3 равен
С=А2х2×В2х3 Матрицаның өлшемi неге тең
A) С2х3
B) С2х2
C) С1х2
D) С1х3
E) С4х6
65.Размер матрицы С=А5х2×В2х4 равен
С=А5х2×В2х4 Матрицаның өлшемi неге тең
A) С5х4
B) С2х2
C) С7х8
D) С10х8
E) С3х2
66.Размер матрицы С=А2х1×В2х3 равен
С=А2х1×В2х3 Матрицаның өлшемi неге тең
A) Нет правильного ответа
Дұрыс жауабы жоқ
B) С2х3
C) С2х2
D) С1х2
E) С1х3А1А2+В1В2+С1С2=0
67.Размер матрицы С=А4х2×В3х4 равен:
С=А4х2×В3х4 матрицаның өлшемi неге тең:
A) Нет правильного ответа
Дұрыс жауабы жоқ
B) С2х3
C) С4х4
D) С4х3
E) С2х4
68.Даны матрицы А=  и В=
и В= 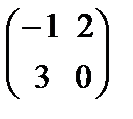 их сумма равна
их сумма равна
Берiлген А=  жґне В=
жґне В= 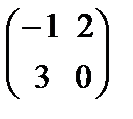 матрицасының қосындысы тең
матрицасының қосындысы тең
A) 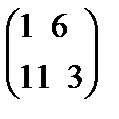
B) 
C) 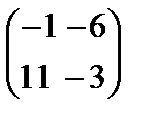
D) 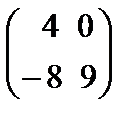
E) 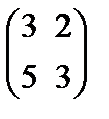
69.Даны матрицы А=  и В=
и В= 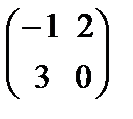 их разность равна
их разность равна
Берiлген А=  жґне В=
жґне В= 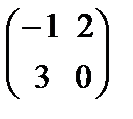 матрицасының айырмасы тең
матрицасының айырмасы тең
A) 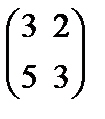
B) 
C) 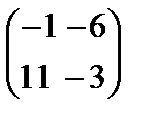
D) 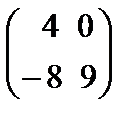
E) 
70.Даны матрицы А=  и В=
и В= 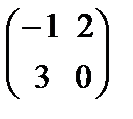 их произведение равно
их произведение равно
Берiлген А=  жґне В=
жґне В= 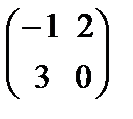 матрицасының көбейтiндiсi тең
матрицасының көбейтiндiсi тең
A) 
B) 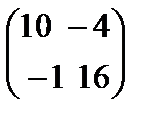
C) 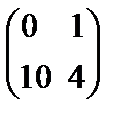
D) 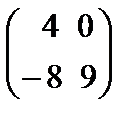
E) 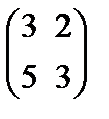
71.Даны матрицы А= 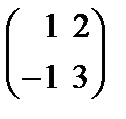 и В=
и В= 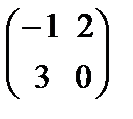 их сумма равна
их сумма равна
Берiлген А= 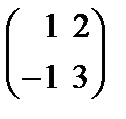 жґне В=
жґне В= 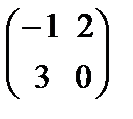 матрицасының қосындысы тең
матрицасының қосындысы тең
A) 
B) 
C) 
D) 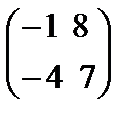
E) 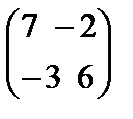
72.Даны матрицы А= 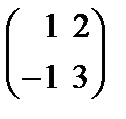 и В=
и В= 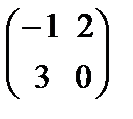 их разность равна
их разность равна
A) 
B) 
C) 
D) 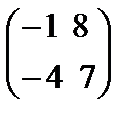
E) 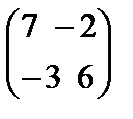
73.Даны матрицы А= 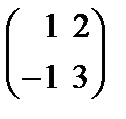 и В=
и В= 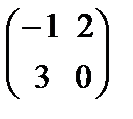 их произведение равно
их произведение равно
Берiлген А= 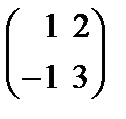 жґне В=
жґне В= 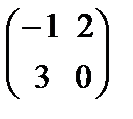 матрицасының көбейтiндiсi тең
матрицасының көбейтiндiсi тең
A) 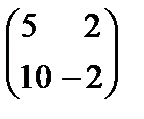
B) 
C) 
D) 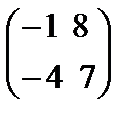
E) 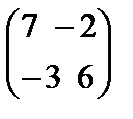
74.Дана матрица А= 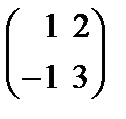 , то А2 равна
, то А2 равна
Берiлген А= 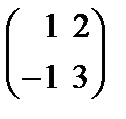 ,матрицасының квадраты А2 тең
,матрицасының квадраты А2 тең
A) 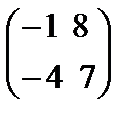
B) 
C) 
D) 
E) 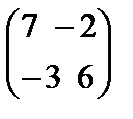
75.Дана матрица В= 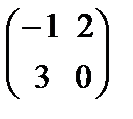 , то В2 равна
, то В2 равна
Берiлген В= 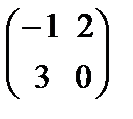 ,матрицасының квадраты В2тең
,матрицасының квадраты В2тең
A) 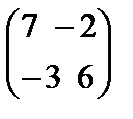
B) 
C) 
D) 
E) 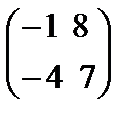
76.Даны матрицы А= 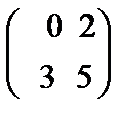 и В=
и В=  их произведение равно
их произведение равно
Берiлген А= 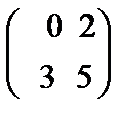 жґне В=
жґне В=  матрицасының көбейтiндiсi тең
матрицасының көбейтiндiсi тең
A) 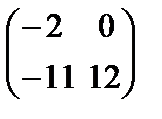
B) 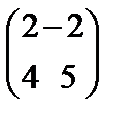
C) 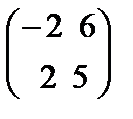
D) 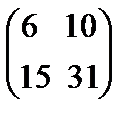
E) 
77.Дана матрица А= 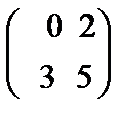 , то А2 равна
, то А2 равна
Берiлген А= 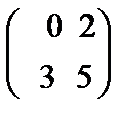 ,матрицасының А2 квадраты тең
,матрицасының А2 квадраты тең
A) 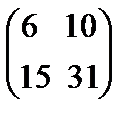
B) 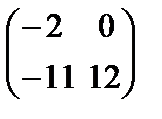
C) 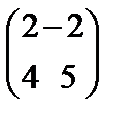
D) 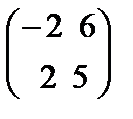
E) 
78.Дана матрица В=  , то В2 равна
, то В2 равна
Берiлген В=  ,матрицасының В2 квадраты тең
,матрицасының В2 квадраты тең
A) 
B) 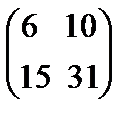
C) 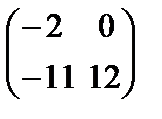
D) 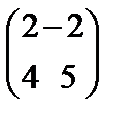
E) 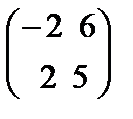
79.Даны матрицы А= 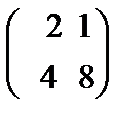 и В=
и В=  их произведение равна
их произведение равна
Берiлген А= 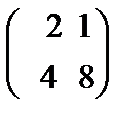 жґне В=
жґне В=  матрицаларының көбейтiндiсi теє
матрицаларының көбейтiндiсi теє
A) 
B) 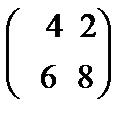
C) 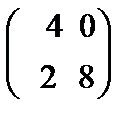
D) 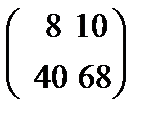
E) 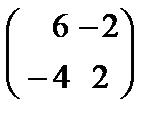
80.Даны матрицы А= 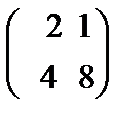 и В=
и В=  их сумма равна
их сумма равна
Берiлген А= 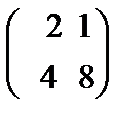 жґне В=
жґне В=  матрицаларының көбейтiндiсi
матрицаларының көбейтiндiсi
A) 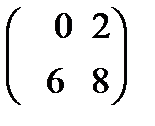
B) 
C) 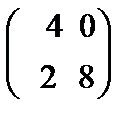
D) 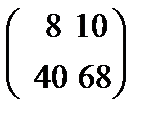
E) 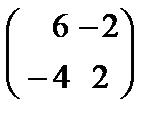
81.Даны матрицы А= 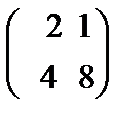 и В=
и В=  их разность равна
их разность равна
Берiлген А= 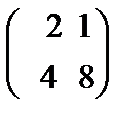 жґне В=
жґне В=  матрицаларының айырмасы тең
матрицаларының айырмасы тең
A) 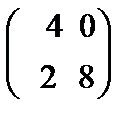
B) 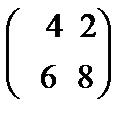
C) 
D) 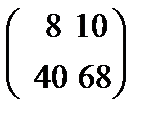
E) 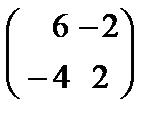
82.Дана матрица В=  , то В2 равна
, то В2 равна
В=  ,берiлген,онда В2 тең
,берiлген,онда В2 тең
A) 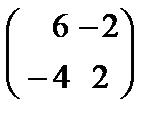
B) 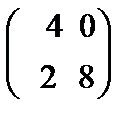
C) 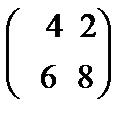
D) 
E) 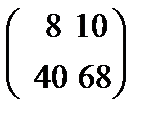
83.Определитель матрицы К=  равен
равен
Матрицаныє анықтауышы тең
A) det K=0
B) det K=9
C) det K=3
D) det K= -21
E) det K= 21
84.Определитель матрицы К= 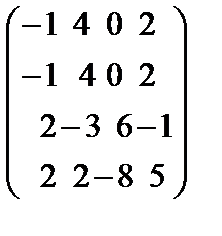 равен
равен
Матрицаның анықтауышы тең
A) det K=0
B) det K=9
C) det K=3
D) det K= -21
E) det K= 21
85.Определитель матрицы К=  равен
равен
Матрицаның анықтауышы тең
A) det K=0
B) det K=9
C) det K=3
D) det K= -21
E) det K= 21
86.Матрица А-1 называется обратной для матрицы А (квадратная порядка n), если выполняется условие
A) АА-1= А-1А= Е
B) А+А-1=Е
C) А-А-1=Е
D) АА-1=АТ
E) АТА-1=АТ=E
87.Размер матрицы К=М2х4×В4х2 равен
Матрицаның К=М2х4×В4х2 өлшемi неге тең
A) К2х2
B)К2х4
C)К4х2
D) К4х4
E) К4х1
88.Размер матрицы К=М3х4×В4х2 равен
Матрицаның К=М3х4×В4х2 өлшемi неге тең
A) К3х2
B) К2х3
C) К4х2
D) К4х4
E) К4х3
89.Размер матрицы К=М2х1×В1х3 равен
Матрицаның К=М2х1×В1х3 өлшемi неге тең
A) К2х3
B) К1х1
C) К1х3
D) К3х1
E) К3х2
90.Размер матрицы К=М5х4×В4х1 равен
Матрицаның К=М5х4×В4х1 өлшемi неге тең
A) К5х1
B) К5х4
C) К4х5
D) К1х5
E) К4х
91.Найти алгебраическое дополнение А12 матрицы 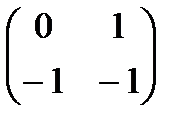
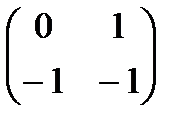 матрицасының А12 алгебралық толықтауышын тап
матрицасының А12 алгебралық толықтауышын тап




