(-2,203;9,405).
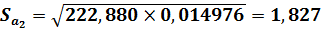
Нехай β- інтервал довіри, t0,05=2,145, тоді:
4,899-2,145*1,827< β <4,899+2,145*1,827
Lt;β< 8,818
Отже, таким чином з ймовірністю 95% параметр а1 знаходиться в інтервалі
(0,980; 8,818).
Знайдемо множинний коефіцієнт кореляції.
R=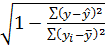 
= 
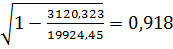
Оскільки R→1, то зв’язок між Yта факторами X тісний.
Перевіримо коефіцієнт кореляції на суттєвість за критерієм Стьюдента. Сформулюємо Н0: R=0, R- не суттєвий
Використаємо t-критерій:
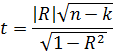
Знайдемо фактичне значення критерію Стьюдента:
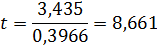
Порівняємо фактичне значення t-критерію з табличним:
tфакт> tтабл
8,661> 2,145
Отже, коеф кореляції є суттєвий.
Тепер знайдемо множинний коефіцієнт детермінації.
D=R2=0,9182=0,843
Перевіримо суттєвість множинного коефіцієнта детермінації. Для цього використаємо F-критерій Фішера.
Сформулюємо нульову гіпотезу Н0: D=0, не суттєвий
Побудуємо F-критерій:
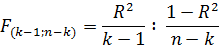
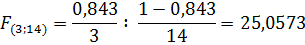
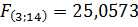
Знайдемо табличне значення F-критерію для рівня значущості α = 0,05 (рівень ймовірності P=1-α=1-0,05= 0,95). Для α і кількості ступенів вільності k-1; n-k табличне значення буде таким:
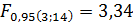
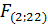25,0573> 
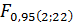3,34
Фактичне значення F-критерію перевищує табличне, тому коефіцієнт множинної детермінації суттєвий, тобто ≠0. Суттєвість результативної ознаки з обома факторами доведена.
Перевіримо побудовану модель на адекватність за критерієм Фішера
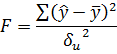
Знайдемо фактичне значення критерію Фішера:
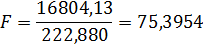
Порівняємо фактичне значення з табличним:
75,3954> 3,34
Оскільки фактичне значення F-критеріюбільше за табличне, то дана модель адекватна.
Будуємо точковий прогноз для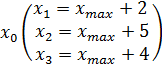 
:
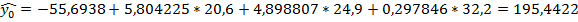
Побудова множинної лінійної моделі в програмі MS Excel
Регресійна статистика
| Регрессионная статистика | |
| Множественный R | 0,918363931 |
| R-квадрат | 0,84339231 |
| Нормированный R-квадрат | 0,809833519 |
| Стандартная ошибка | 14,92917252 |
| Наблюдения |
Множинний коефіцієнт кореляції відображує тісноту зв’язку між результативною ознакою і всіма факторами що вивчаються, оскільки він прямує до «1» (R=0, 918363931), то зв'язок тісний.
Коефіцієнт детермінації (R2) показує, що варіація результативної ознаки У на 84,33% обумовлена впливом трьох факторів Х1, Х2 та Х3. Решта варіації – 15,67% - це вплив випадкових не врахованих факторів.
Дисперсійний аналіз
| df | SS | MS | F | Значимость F | |
| Регрессия | 16804,13 | 5601,377 | 25,0573215 | 6,7435Е-06 | |
| Остаток | 3120,323 | 222,8802 | |||
| Итого | 19924,45 |
df – ступені вільності
SS – суми квадратів відхилень
MS – середні суми квадратів відхилень з урахуванням числа ступенів вільності
F – значення критерія Фішера з рівнем довіри 95%
Значимість F – якщо значення цього показника менше за 0,05 то побудована регресійна модель адекватна
Таблиця 6. Значення параметрів множинного кореляційного рівняння
Дисперсійний аналіз (таблиця 2)
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y | -55,69376992 | 28,16683 | -1,97728 | 0,068043 | -116,105608 | 4,71806852 | -116,105608 | 4,71806852 |
| X 1 | 5,804224765 | 1,678866 | 3,45723 | 0,003849 | 2,203416084 | 9,40503345 | 2,203416084 | 9,40503345 |
| X 2 | 4,898807178 | 1,826989 | 2,681356 | 2,681356 | 0,980305773 | 8,81730858 | 0,980305773 | 8,81730858 |
| X 3 | 0,29784598 | 1,139242 | 0,261442 | 0,261442 | -2,145585525 | 2,74127749 | -2,14558552 | 2,74127749 |
Отже, обчислене значення критерія є більшим, ніж критичне. Звідси з ймовірністю 0,95 можна зробити висновок про суттєвість множинного коефіцієнта детермінації. Можна зазначити, що досліджувані фактори разом суттєво впливають на варіацію роздрібного товарообігу
