Для каждого заданного значения 
из области сходимости функционального ряда (1) 
, где 
– п -ый остаток ряда (1). По определению предела последовательности это означает, что для любого числа 
можно указать номер 
, такой, что для всех номеров 
и данного выполняется неравенство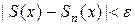 
. Номер зависит не только от выбора числа 
, но, вообще говоря, и от выбора точки .
Определение. Если для любого числа можно указать номер такой, что для всех номеров и всех из некоторого множества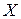 
выполняется неравенство 
, то ряд (1) называется равномерно сходящимся на множестве .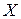
Геометрически определение равномерной сходимости иллюстрируется рисунком.
Равномерно сходящиеся функциональные ряды обладают следующими общими свойствами.
Теорема 1. Если члены равномерно сходящегося ряда (1) непрерывны на множестве 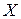, то его сумма также непрерывна на .
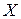Теорема 2. Если на отрезке 
:
а) члены ряда (1) непрерывны;
б) ряд (1) равномерно сходится,
то его сумма 
интегрируема на , и выполняется равенство
. (3)
В этом случае говорят, что ряд (1) можно интегрировать почленно на отрезке .
Теорема 3. Если на отрезке :
а) ряд (1) сходится;
б) его члены имеют непрерывные производные;
в) ряд из производных равномерно сходится,
то сумма ряда (1) дифференцируема на , и выполняется равенство
. (4)
В этом случае говорят, что ряд (1) можно дифференцировать почленно на отрезке .
Значение перечисленных свойств состоит в том, что для равномерно сходящихся функциональных рядов оказываются справедливыми свойства сумм конечного числа функций: «сумма непрерывных функций непрерывна», «производная суммы равна сумме производных», «интеграл от суммы равен сумме интегралов». К рядам, сходящимся неравномерно, эти свойства применять, вообще говоря, нельзя.
Степенные ряды
Определение. Степенным рядом называется функциональный ряд вида
, (5)
где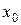 
– некоторое заданное число. Постоянные числа 
, называются коэффициентами степенного ряда (5).
Ряд (5) называют также рядом по степеням двучлена 
.
При 
имеем ряд по степеням :
. (6)
Степенной ряд общего вида (5) всегда можно привести к виду (6) заменой двучлена 
, поэтому далее будем рассматривать степенные ряды вида (6) (по степеням ).
Очевидно, что любой ряд вида (6) сходится при 
.
Теорема 4 (Абель). Если ряд (6) сходится в точке 
, то он сходится, притом абсолютно, во всех точках таких, что 
. Если ряд (6) расходится в точке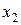 
, то он расходится во всех точках таких, что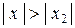 
.
Теорема 5. Областью сходимости степенного ряда (6) является некоторый промежуток 
с включёнными или невключёнными концами и центром в точке . На интервале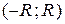 
ряд сходится абсолютно, вне промежутка – расходится.
Определение. Интервал 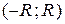, определённый в теореме 5, называется интервалом сходимости степенного ряда (6), а число 
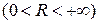– его радиусом сходимости.
Интервал сходимости можно записать в виде неравенства 
.
Замечание. Замена на двучлен даёт интервал сходимости степенного ряда общего вида (5): 
, или 
.
Если степенной ряд (6) сходится при любом значении , то его интервалом сходимости является вся числовая ось 
(ниже пример 3). В этом случае записывают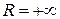 
. В другом крайнем случае, когда является единственной точкой сходимости, полагают 
(ниже пример 4); интервал сходимости тогда вырождается в точку . Таким образом, любой степенной ряд имеет свой радиус сходимости.
Вопрос. Как найти интервал и радиус сходимости?
Ответ. Если коэффициенты ряда (6) 
, то для нахождения интервала сходимости обычно пользуются признаком Даламбера в формулировке для абсолютной сходимости (см.), при условии, что 
.
Если коэффициенты ряда (6) , то радиус сходимости находится по формулам 
или 
.
Пример 2. Функциональный ряд 
является степенным рядом вида (6). Его интервал сходимости 
найден в примере 1. Получим то же с помощью признака Даламбера. При 
для сходимости. Радиус сходимости 
.
Пример 3. Найти интервал сходимости ряда
(
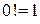). (7)
Имеем: 
, следовательно, интервал сходимости ряда (7) – вся числовая ось .
Пример 4. Найти радиус сходимости ряда
.
Имеем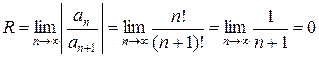 
. Данный ряд сходится только при .
Вопрос. Каково поведение степенного ряда (6) на концах его интервала сходимост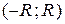и при 
?
Ответ. Поведение степенных рядов (6) на концах интервала сходимости может быть различным: в точках 
ряд может расходиться или сходиться, абсолютно или условно. Поэтому интервал сходимости степенного ряда не всегда совпадает с его областью сходимости? Если в задаче предлагается найти именно область сходимости, то после нахождения интервала сходимости обязательно требуется выполнить исследование ряда на сходимость в концах интервала.
Теорема 6. Степенной ряд (6) сходится равномерно на любом отрезке 
, целиком содержащемся внутри его интервала сходимости .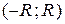
Из теорем 1 – 6 следуют общие свойства степенных рядов:
1. Сумма степенного ряда непрерывна внутри его интервала сходимости.
2. Степенной ряд можно почленно интегрировать по любому промежутку, лежащему внутри его интервала сходимости.
3. Степенной ряд можно почленно дифференцировать в любой точке, лежащей внутри его интервала сходимости.
4. При почленном интегрировании или дифференцировании степенного ряда радиус сходимости не изменяется.
Из свойства 3 следует также
5. В своём интервале сходимости степенной ряд можно почленно дифференцировать любое число раз. Говорят поэтому, что сумма степенного ряда есть функция, бесконечно дифференцируемая на его интервале сходимости.
