Числовые ряды
Определение числового ряда и его суммы
Образуем из элементов числовой последовательности 
символ суммы
(1)
Определение. Выражение (1) называется числовым рядом.
Число 
называется первым членом ряда (1), 
– вторым членом; выражение 
называется общим членом ряда (1). Ряд считается заданным, если задана формула его общего члена. Чтобы определить, скажем, пятый член ряда, требуется подставить 
в формулу общего члена. Это позволяет кратко записывать ряд (1) с помощью символа суммирования в виде 
.
Как правило, первый член ряда имеет номер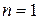 
, хотя ряд может начинаться и с любого другого члена последовательности 
.
Определение. Сумма 
первых 
членов ряда (1) называется его n- ой частичной суммой.
Величины 
, 
,…, 
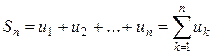,… образуют последовательность 
частичных сумм ряда (1).
Определение. Если при 
существует конечный предел 
последовательностичастичных сумм ряда (1), то ряд (1) называется сходящимся, число 
называется суммой ряда (1), и записывают тогда: 
. Если 
не существует (в частности, бесконечен), то ряд (1) называется расходящимся. Для расходящегося ряда понятие суммы не определено.
Пример 1. Ряд 
. Его -ая частичная сумма 
при . Ряд расходится.
Пример 2. Ряд 
. Частичная сумма 
, 
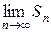не существует. Ряд расходится.
Пример 3. Числовой ряд, составленный из членов геометрической прогрессии, называется геометрическим:
.
Здесь 
– первый член геометрической прогрессии, 
– её знаменатель. С помощью известной формулы суммы первых членов геометрической прогрессии 
можно показать, что геометрический ряд сходится, если 
, и его сумма равна 
.
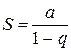Простейшие свойства сходящихся рядов
Теорема 1 (о почленном умножении ряда на число). Если ряд сходится и имеет сумму , то ряд 
, где с – постоянная, также сходится и имеет сумму 
.
Теорема 2 (о почленном сложении сходящихся рядов). Пусть числовые ряды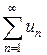 
и 
сходятся и имеют суммы 
и 
соответственно. Тогда ряд 
также сходится, и его сумма равна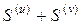 
.
Определение. Если у ряда (1) отбросить k первых членов, то получится новый ряд 
, называемый k -ым остатком ряда (1).
Теорема 3. Ряд (1) и любой из его остатков либо одновременно сходятся, либо одновременно расходятся.
Таким образом, если в ряде отбросить, добавить или изменить конечное число членов, то сходимость (или расходимость) этого ряда не изменится. При этом если ряд сходился, то его сумма, вообще говоря, изменится.
Сумма k -го остатка сходящегося ряда обозначается 
. Для суммы сходящегося ряда справедливо равенство 
. Отсюда следует, что если вычислить k -ую частичную сумму 
сходящегося ряда и взять её в качестве приближённого значения суммы ряда S, то ошибка составит величину k -го остатка 
. При этом имеем 
.
