1. Уравнения с разделенными переменными.
Уравнением с разделенными переменными называется ДУ вида M (x) dx + N (y) dy = 0. Решается интегрированием
.
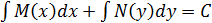Пример.
Семейство интегральных кривых представляет собой концентрические окружности с центром в начале координат.
2. Уравнения с разделяющимися переменными.
Это ДУ вида 
.
Решение
;
; 
Пример.
.
Решение
, 
, 
.
Семейство интегральных кривых представляет собой семейство прямых, проходящих через начало координат.
Замечание: Уравнением с разделяющимися переменными будет также уравнение вида: 
или 
3. Однородные уравнения.
Функция f (x, y) называется однородной функцией степени k относительно переменных x и y, если при любом t справедливо тождество f (tx, ty) = tk 
f (x, y).
Примеры.
1) 
= 
.
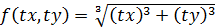Следовательно, исходная функция является однородной первой степени.
2) 
.
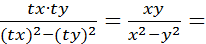
Следовательно, исходная функция является однородной нулевой степени.
ДУ первого порядка y’ = f (x, y) называется однородным относительно переменных х и у, если функция f (x, y) является однородной функцией нулевой степени относительно переменных х и у.
Решение
По условию 
.
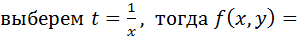
Исходное уравнение примет вид 
.
Сделаем замену: 
(производная произведения). При этом исходное уравнение 
будет уравнением с разделяющимися переменными.
Пример.
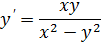
Ранее было показано, что функция в правой части является однородной нулевой степени => данное уравнение однородное. Делаем замену: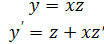 
Вернемся к замене 
Тогда, применив свойства логарифмов, получим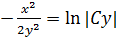 
– общий интеграл (общее решение в неявном виде).
Замечание: Однородным ДУ первого порядка будет также уравнение вида 
в том случае, если функции M и N являются однородными функциями одной степени. Решение также заменой 
, при этом 
.
4. Линейные ДУ первого порядка
Линейным ДУ первого порядка называется ДУ первого порядка, линейное относительно неизвестной функции и ее производной: 
, где p (x), f (x) – заданные непрерывные функции.
Если f(x) = 0, то уравнение 
называется линейным однородным уравнением первого порядка (ЛОДУ первого порядка).
Если f(x) ≠0, то уравнением 
называется линейным неоднородным уравнением первого порядка (ЛНДУ первого порядка).
ЛОДУ первого порядка является уравнением с разделяющимися переменными.
Решение ЛНДУ будем искать в виде произведения двух функций y = u (x) ∙ v (x) или 
, тогда 
. Подставим в исходное уравнение: 
; 
Функцию v выбираем произвольно, поэтому выберем так, чтобы выражение в скобках равнялось нулю: 
, это уравнение с разделяющимися переменными. Решая его, найдем функцию v, при этом C считаем равной 0. Далее найденную функцию v будем подставлять в последнее уравнение, получим: 
– это также уравнение с разделяющимися переменными. Решая его, найдем функцию u, при этом C некоторая постоянная. Вернувшись к замене y = u ∙ v, получим общее решение исходного уравнения.
Пример.
это ЛНДУ, делаем замену 
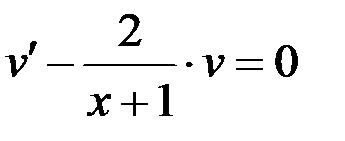- это уравнение с разделяющимися переменными
(считаем постоянную равной 0). Возвращаемся к исходному уравнению
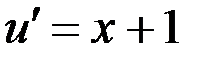
– общее решение исходного уравнения.
5. Уравнения в полных дифференциалах
Известно, что выражение M (x, y) dx + N (x, y) dy является полным дифференциалом некоторой функции тогда и только тогда, когда выполняется следующее равенство частных производных: 
.
ДУ первого порядка вида M (x, y) dx + N (x, y) dy = 0 называется уравнением в полных дифференциалах, если M и N непрерывные дифференцируемые функции, для которых выполняется: .
Один из способов решения уравнений в полных дифференциалах состоит в том, что задаются произвольные x 0, y 0 (из области определения) и общий интеграл уравнения находится по одной из формул:
,
или 
Пример.
,
Следовательно, это уравнение в полных дифференциалах. Выберем x 0= 0; y 0= 1.
3. Линейные дифференциальные
уравнения второго порядка
ДУ второго порядка имеет вид:
Общее решение ДУ второго порядка имеет вид:
.
ДУ второго порядка вида 
, где p (x), 
, f (x) – непрерывные функции от х, называется линейным неоднородным ДУ второго порядка (ЛНДУ). Функции p (x) и q (x) называют коэффициентами уравнения. Если f (x) = 0, то уравнение 
(2), называется линейным однородным ДУ второго порядка (ЛОДУ). Если уравнение (2) имеет те же коэффициенты, что и уравнение (1), то уравнение (2) называется однородным уравнением соответствующим неоднородному уравнению (1).
Функции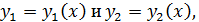 
определенные и непрерывные на некотором интервале, называются линейно зависимыми на этом интервале, если существуют числа 
(неравные одновременно 0) такие, что для всех х из рассматриваемого интервала выполняется тождество: 
. Если указанное тождество имеет место только при 
, то функции y1 и y2 называют линейно независимыми.
Теорема 1 (об общем решении ЛОДУ второго порядка). Если 
линейно независимые частные решения ЛОДУ второго порядка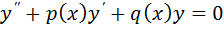 
, то общее решение этого уравнения имеет вид 
– произвольные постоянные.
Замечание: условно данную теорему можно записать: 
(«оо» – общее решение однородного уравнения, «чо» – частное решение однородного уравнения).
Определителем Вронского (или вронскианом) двух функций 
называется определитель: 
.
Теорема 2. Если функции линейно независимы на некотором интервале, то определитель Вронского, составленный из них, отличен от нуля на этом интервале.
Пример.
– это ЛОДУ второго порядка.
Легко заметить, что его частными решениями будут
.
Составим для этих функций определитель Вронского: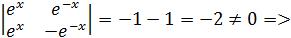 
данные решения линейно независимы, тогда 
Теорема 3 (об общем решении ЛНДУ второго порядка). Общее решение ЛДНУ второго порядка равно сумме общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения 
(«он» – общее решение неоднородного уравнения, «чн» – частное решение неоднородного уравнения).
В общем случае задача отыскания частного решения ЛНДУ является сложной. Можно найти частное решение методом вариации произвольных постоянных, если известно общее решение соотвествующего ЛОДУ 
. Суть метода в том, что частное решение неоднородного уравнения будем искать в ви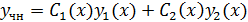де 
, где 
– некоторые искомые функции от х.
Находить будем подстановкой 
в исходное уравнение. Будем подбирать так, чтобы
Главный определитель системы является определителем Вронского для функций y 1, y 2, а так как они линейно независимы, то определитель Вронского отличен от нуля => система имеет единственное решение относительно C' 1(x) и C' 2(x). Далее, интегрируя, найдем C 1(x) и C 2(x) и можем получить у чн и у он.
4. ЛОДУ второго порядка
с постоянными коэффициентами
ЛОДУ второго порядка с постоянными коэффициентами имеет вид:
, (1)
где p, q – некоторые действительные числа.
Уравнение
(2)
– называется характеристическим уравнением уравнения (1).
Теорема 1 (о решениях ЛОДУ второго порядка с постоянными коэффициентами):
1. Если k – вещественный корень уравнения (2), то 
будетрешением уравнения (1).
2. Если числа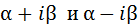 
– комплексные корни уравнения (2), то 
- решения уравнения (1).
Замечание: если k - вещественный корень уравнения (2), при этом дискриминант равен 0, то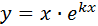 
будетрешением уравнения (1).
Теорема 2 (об общем решении ЛОДУ второго порядка с постоянными коэффициентами).
1. Если корни уравнения (2) действительные различные (D > 0, k1 ≠ k2), то общее решение уравнения (1) имеет вид: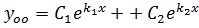 
.
2. Если корни уравнения (2) действительные равные (D = 0,
k1 = k2 = k), то общее решение уравнения (1) имеет вид: 
3. Если корни уравнения (2) комплексные (D < 0, 
, то общее решение уравнения (1) имеет вид:
.
Примеры.
Найти общее решение уравнений.
1) 
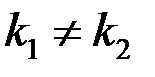Þ 
2) 
3) 
