Пусть функция z = f (x; y) определена в некоторой окрестности точки М 0(x 0; y 0).
М 0(x 0; y 0) – точка локального максимума функции z = f (x; y), если существует такая окрестность точки М 0, что для всех точек М (x; y) из этой окрестности выполняется: f (x; y) ≤ f (x 0; y 0).
М 0(x0; y 0) – точка локального минимума функции z = f (x; y), если существует такая окрестность точки М 0, что для всех точек М (x; y) из этой окрестности выполняется: f (x; y) ≥ f (x 0; y 0).
Точки локального максимума и локального минимума – точки локальных экстремумов.
Локальный характер экстремума – выполнимость вышеперечисленных условий лишь в некоторой окрестности точки.
Теорема 1 (необходимое условие экстремума). Если функция
z = f (x; y)дифференцируема в точке М 0 (x 0; y 0) и имеет в этой точке экстремум, то частные производные в этой точке равны 0:
z'x (x 0; y 0) = z'y (x 0; y 0) = 0.
Замечание. Функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует.
Точки, в которых частные производные равны 0 или не существуют, называются критическими точками. Точки экстремума следует искать среди критических точек.
Теорема 2 (достаточное условие экстремума). Пусть функция z = f (x; y)определена в некоторой окрестности критической точки (x 0; y 0) и имеет в этой точке непрерывные частные производные второго порядка:
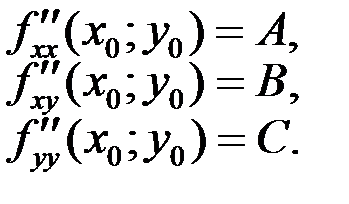
Тогда, если
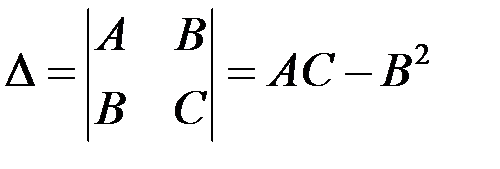
1) ∆ > 0, то в точке М 0 функция z = f (x; y)имеет экстремум, причем при А < 0 – локальный максимум, при А > 0 – локальный минимум;
2) ∆ < 0, то в точке М 0 экстремума нет;
3) ∆ = 0, то точка М 0 может быть, а может и не быть точкой экстремума. Необходимы дополнительные исследования.
Пример.
Найти точки экстремума функции z = x 2 + xy + y 2 – 2 x – 3 y.
z'x = 2 x + y – 2,
z'y = x + 2 y – 3.
2 x + y – 2 = 0
x + 2 y – 3 = 0
y = 4/3, x = 1/3.
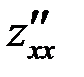 = 2 = A,
= 2 = A, 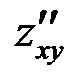 = 1 = B, z''yy = 2 = C
= 1 = B, z''yy = 2 = C 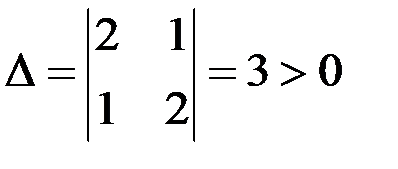 .
.
Следовательно, в точке 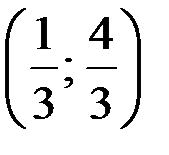 локальный минимум.
локальный минимум.
Условный экстремум
Требуется найти экстремум функции z = f (x; y)при условии g (x; y) = 0. При этом z = f (x; y)называется целевой функцией,
g (x; y) = 0 – уравнением связи.
Экстремум – условный.
Функция g (x; y) предполагается известной.
Способы нахождения условного экстремума:
1) Метод подстановки
Из уравнения g (x; y) = 0 выражаем одну из переменных y = φ(x) и подставляем в функцию z = f (x; y) = f (x;φ(x)),получим функцию одной переменной.
Этот метод применим, когда уравнение связи легко разрешить относительно одной из переменных.
Пример.
Найти экстремум функции z = x 2 – 3 xy+ 12 x при условии6 –
– 2 x – 3 y = 0.
y = 2 – 2/3 x, тогда z = x 2 – 6 x + 2 x 2 + 12 x = 3 x 2 + 6 x.
z' = 6 x + 6 = 0, x = -1, y = 8/3.
Следовательно, в точке (-1;8/3) условный экстремум.
2) Метод множителей Лагранжа
Рассмотрим функцию трех переменных:
L (x; y; λ) = f (x; y) + λ g(x; y).
Это функция Лагранжа, где λ – множитель Лагранжа.
Для нахождения условного экстремума функции z = f (x; y)требуется найти локальный экстремум функции L (x; y; λ). Для этого необходимо решить систему уравнений:
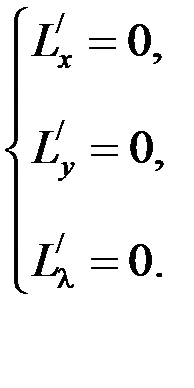
Пример.
Найти экстремум функции z= x 2 – 3 xy + 12 x при условии 6 – 2 x – – 3 y = 0.
Составим функцию Лагранжа:
L (x; y; λ) = x 2 – 3 xy + 12 x + λ(6 – 2 x – 3 y)
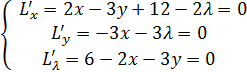
Решая данную систему, получим: 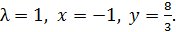
Следовательно, в точке (-1;8/3) условный экстремум.
В заключение следует отметить, что метод Лагранжа позволяет находить условные экстремумы. Но вопрос о том, максимум это или минимум, остается открытым. При решении экономических задач, однако, часто сам характер задачи подсказывает, что мы можем ожидать – максимум или минимум. Кроме того, существует простой способ анализа точки экстремума, вытекающий из самого определения.
Пусть (x 0; y 0) – точка условного экстремума, а f (x 0; y 0) – соответствующее значение целевой функции. Берется точка (x; y) близкая к точке (x 0; y 0) и вычисляется значение в ней целевой функции.
Если f (x; y) < f (x 0; y 0), то в точке (x 0; y 0) локальный максимум; если f (x; y) > f (x 0; y 0), то в точке (x 0; y 0) локальный минимум.
В настоящее время существует большое количество програм-мных пакетов, позволяющих численно решать на компьютерах задачи как условной, так и безусловной оптимизации.
РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА
КОНТРОЛЬНОЙ РАБОТЫ
Задача 1
Найти и изобразить область определения функции:
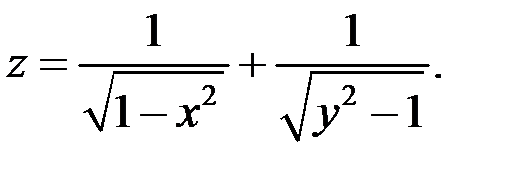
| y |
| x |
| -1 |
| -1 |

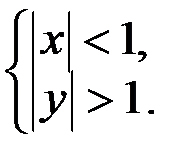
Задача 2
Найти приближенно изменение функции  при изменении x от 2 до 1,94, y от 2 до 2,06.
при изменении x от 2 до 1,94, y от 2 до 2,06.
Решение
Найдем частные производные в точке 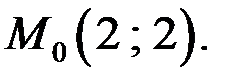
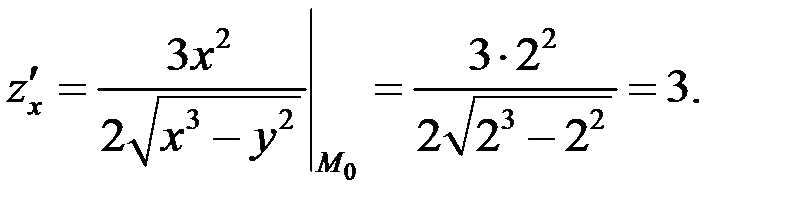
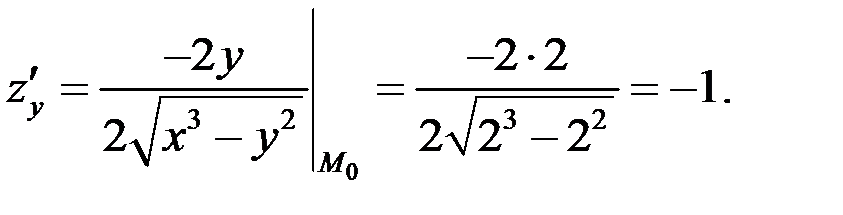

По условию 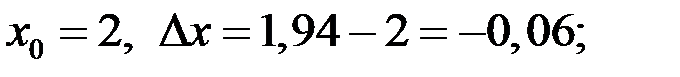

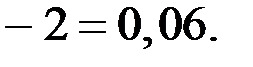 Тогда
Тогда 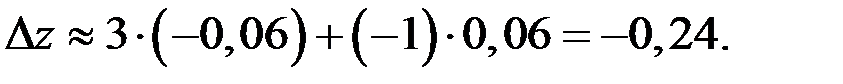
Ответ: – 0,24.
Задача 3
Найти частные производные второго порядка функции 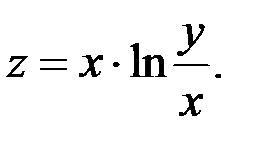
Решение
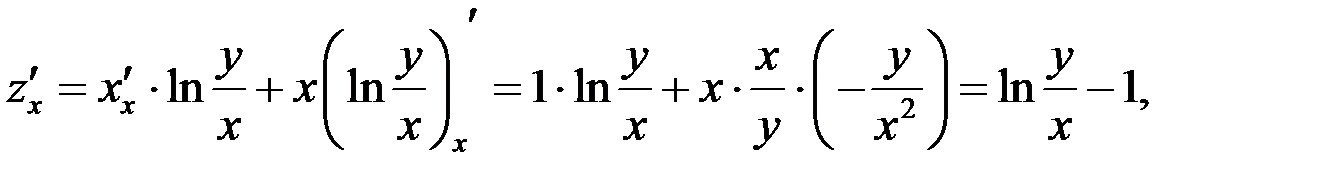

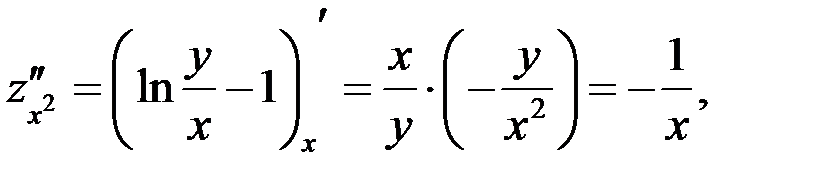
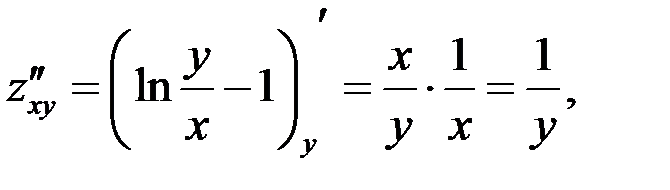
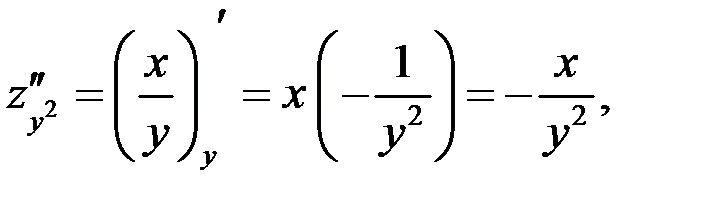
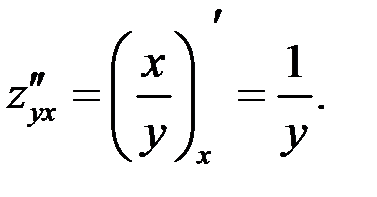
Ответ: 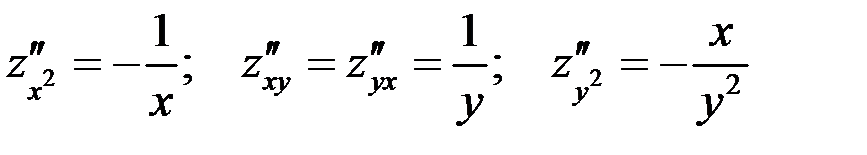 .
.
Задача 4
Написать уравнение касательной плоскости и нормали к поверхности  в точке
в точке 
Решение
Найдем частные производные функции 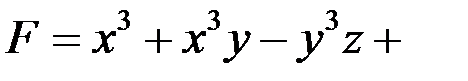
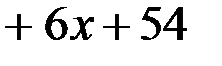 в точке
в точке  .
.

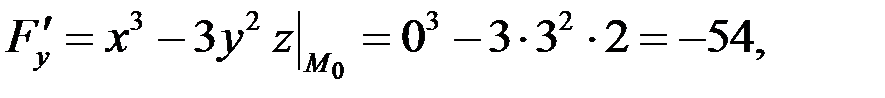
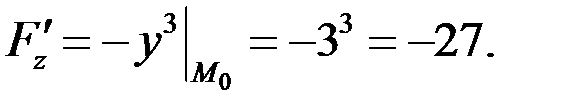
Касательная плоскость определяется уравнением:

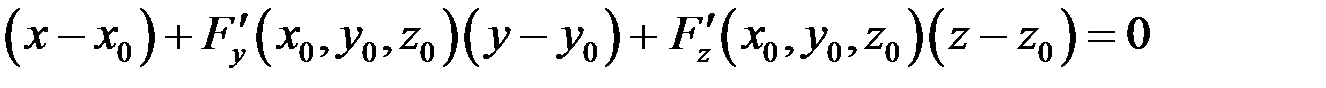
Тогда

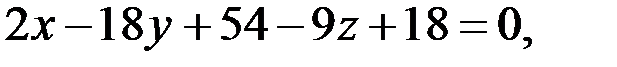
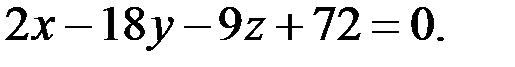
Уравнение нормали имеет вид
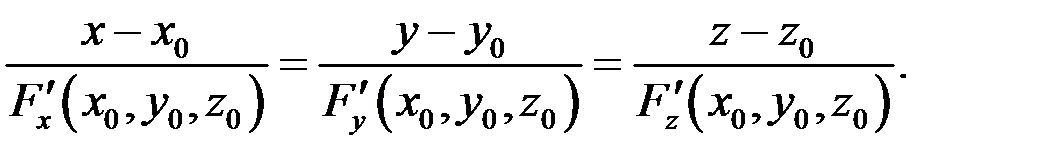
Тогда

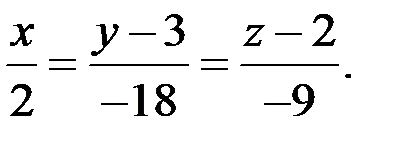
Ответ: уравнение касательной плоскости  ;
;
уравнение нормали  .
.
Задача 5
Найти точки экстремума функции 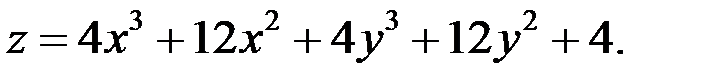
Решение
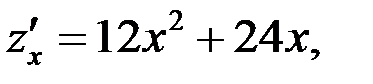
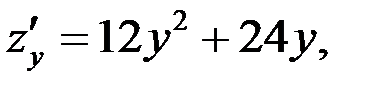


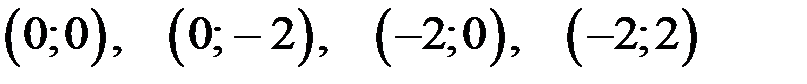 – критические точки.
– критические точки.
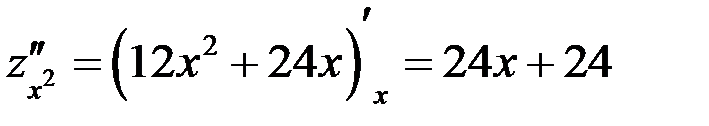
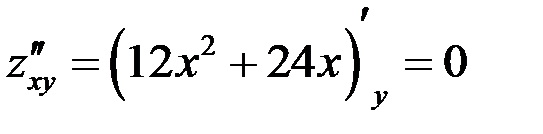

Проверим критические точки на экстремум:
1) 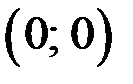
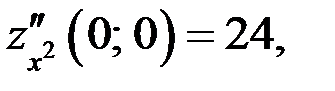
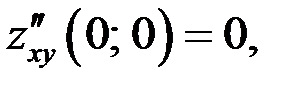

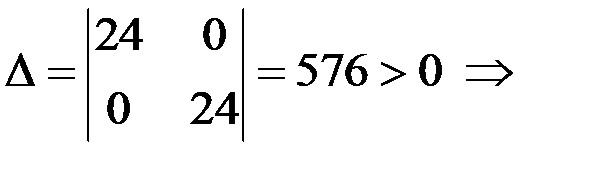 экстремум есть.
экстремум есть.
 в точке
в точке 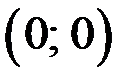 – локальный минимум.
– локальный минимум.
2) 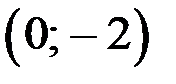

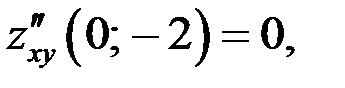
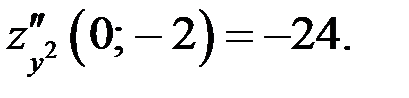
 экстремума нет.
экстремума нет.
3) 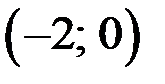
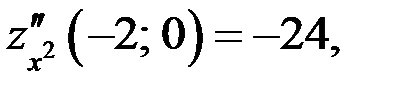
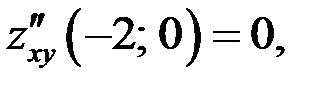
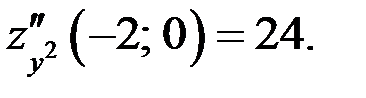
 экстремума нет.
экстремума нет.
4) 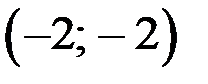

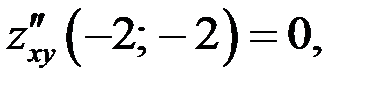
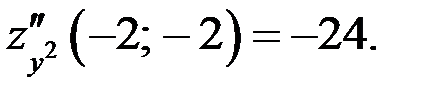
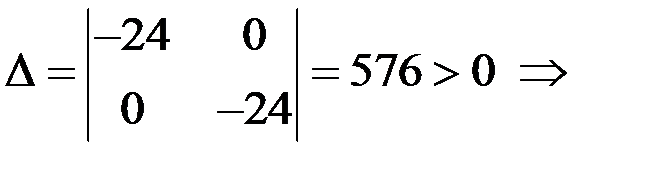 экстремум есть.
экстремум есть.
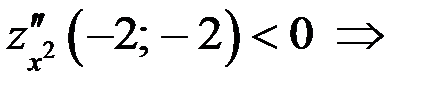 в точке
в точке 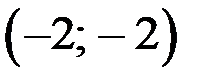 – локальный максимум.
– локальный максимум.
Ответ: функция z имеет в точке  локальный минимум, в точке
локальный минимум, в точке 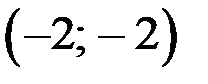 локальный максимум.
локальный максимум.
Контрольная работа 3.2






